
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 6. Тема: Формула Дарси. Закон Пуазейля
|
|
|
|
Тема: Формула Дарси. Закон Пуазейля. Турбулентный режим течения жидкости. Опыт Рейнольдса. Осреднение по Рейнольдсу. Формула Блазиуса. Формула Никурадзе. Профиль скорости при турбулентном режиме течения в трубе.
Определив максимальную и среднюю по сечению трубы скорости, вернемся к определению потерь на трение.
Запишем интегральное уравнение Бернулли для стационарного течения несжимаемой жидкости:
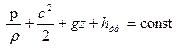 , где постоянная зависит от граничных условий.
, где постоянная зависит от граничных условий.
Запишем интеграл Бернулли для двух сечений: входного «1» и выходного «2»:
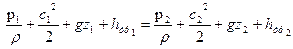 .
.
Полная входная энергия была бы равна полной выходной, если бы не потери на вязкое трение. Запишем иначе:
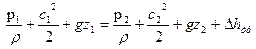 ,
,
где 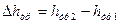 - доля энергии, которая перешла в теплоту под влиянием трения.
- доля энергии, которая перешла в теплоту под влиянием трения.
Все члены в последнем равенстве имеют размерность 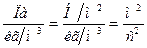 .
.
Выразим 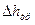 через некую дополнительную потерю давления за счет трения:
через некую дополнительную потерю давления за счет трения: 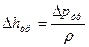 и будем находить именно эти потери давления.
и будем находить именно эти потери давления.
На прошлой лекции было показано, что в круглой трубе давление линейно падает пропорционально длине трубы, отсчитываемой от входа:
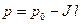 ;
; 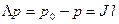 .
.
Но падение давление в трубе как раз и происходит за счет трения, других причин, если площадь поперечного сечения, а следовательно, и скорость постоянны, нет.
Таким образом,
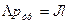 (1)
(1)
 (2)
(2)
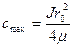 (3)
(3)
Выражаем гидравлический уклон из (3), максимальную скорость заменяем на удвоенную среднюю и подставляем в (1):
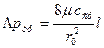 .
.
Обычно с этой формулой производят некоторые преобразования, цель которых – получить справа произведение двух безразмерных комплексов на скоростной напор, имеющий размерность давления.
Кроме того, договоримся далее опускать индекс у средней скорости и обозначать просто: 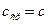 :
:
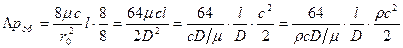 (4)
(4)
Стоящий в знаменателе безразмерный комплекс обозначается 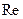 и называется числом или критерием Рейнольдса:
и называется числом или критерием Рейнольдса:
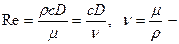 кинематическая вязкость.
кинематическая вязкость.
Окончательно, для потерь давления на трение получаем:
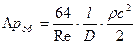 (5)
(5)
Критерии подобия, такие как число Рейнольдса, используются в теории тепломассообмена для вывода т.н. уравнений подобия. По традиции критерии подобия называют в честь великих ученых. Осборн Рейнольдс показал, что подобие течений определяется одинаковыми числами Рейнольдса в них.
Если обозначить в (5) 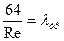 - коэффициент трения, то получим формулу Дарси:
- коэффициент трения, то получим формулу Дарси:
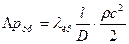 (6)
(6)
Изначально эта формула была получена французским инженером Дарси совсем другим способом – через теорию размерностей. Вообще следует отметить, что в XVIII веке французы очень много занимались гидравликой, что связано со строительством в Париже и других крупных французских городах водопровода и канализации.
Определение коэффициента трения трубы через число Рейнольдса:
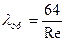 называется законом Пуазейля.
называется законом Пуазейля.
Пуазейль был врачем и получил эту формулу, исследуя кровеносную систему человека.
Согласно закону Дарси потери давления на трение 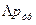 пропорциональны первой степени скорости:
пропорциональны первой степени скорости:
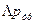
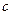 .
.
(Скорость в квадрате в скоростном напоре и скорость в первой степени в знаменателе, в числе Рейнольдса.)
Но в опытах тех же французских инженеров было показано, что пропорциональность 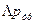
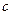 наблюдается не всегда, а довольно редко. Значительно чаще
наблюдается не всегда, а довольно редко. Значительно чаще 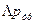
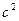 , а бывает еще
, а бывает еще 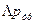
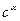 , где
, где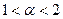 .
.
Разобрался в этом вопросе Рейнольдс, установив опытным путем, что есть два принципиально разных режима течения: ламинарный и турбулентный (есть еще промежуточный, переходный режим).
Все, что говорилось до сих пор, относилось, строго говоря, к ламинарному режиму.
|
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 1521; Нарушение авторских прав?; Мы поможем в написании вашей работы!