Распределение предприятий региона по объему товарооборота

Группы предприятий по объему товарооборота, млн руб.,	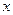Число предприятий	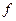Середина интервала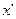
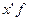
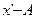
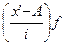
			4		6
До 400			3 150	-200	-2	-18
400—500			5 400	-100	- |	-12
500—600.			4 400
600—700			5 850
Свыше 700			1 500
Итого			-	-	-

Однако в действительности распределение отдельных вариантов в пределах интервала может оказаться неравномерным, и тогда середина интервала будет в той или иной степени отличаться от принятой средней. Это может повлиять на правильность общей средней, исчисленной по данным интервального ряда.

Необходимо отметить, что, хотя мы и используем для расчета средней из интервального ряда формулу средней арифметической взвешенной, исчис­ленная средняя не является точной величиной, так как в результате умножения средних значений групп на их численность мы не получим действительного значения. Сходство исчисленной средней со средней взвешенной лишь в исчислении. Здесь взяты не индивидуальные значения вариант, а условные средние каждой группы. Их взвешивание имеет чисто формальный характер.

Степень расхождения зависит от ряда причин: первой является число вариант. Чем больше число вариант, тем вероятнее, что середина интервала будет мало отличаться от групповой средней. Если же на каждую группу приходится малое число единиц, групповые средние могут находиться не только в середине, но и вблизи верхней либо нижней границы интервала. Если же наблюдений много и они более или менее равномерно распределяются в пределах интервала, то средняя величина в группе будет приближаться к середине интервала. Второй причиной является величина интервала. Если интервал невелик, то и ошибка будет незначительной, так как фактически групповая средняя будет мало отличаться от середины интервала. Третьей причиной является характер распределения. Чем симметричнее распределе­ние, тем ошибка меньше. Размер ошибки зависит и от принципа построения интервального ряда. При равных интервалах середина построения его будет ближе примыкать к средней по данной группе. Кроме того, при наличии открытых интервалов к этому добавляются неточности, связанные с условным установлением неизвестных границ. Поэтому очень важно, чтобы средняя отобразила всю совокупность наблюдений, к которой относится эта средняя.

При этом, отвлекаясь от индивидуальных количественных различий, средняя должна учитывать в полной мере и качество изучаемого признака совокупности.

Средняя гармоническая. Учитывая, что статистические средние всегда выражают качественные свойства изучаемых общественных процессов и явлений, важно правильно выбрать форму средней исходя из взаимосвязи явлений и их признаков. Средняя гармоническая - это величина, обратная средней арифметической, когда z = -1. Когда статистическая информация не содержит частот по отдельным вариантам совокупности, а представлена как их произведение, применяется формула средней гармонической взвешенной.

Так, например, расчет средней цены выражается отношением

Сумма реализации

Средняя цена = --------------------------------------------

Количество реализованных единиц

Величина суммы реализации, т. е. показателя, который находится в числителе исходного отношения, известна. Для определения неизвестной величины - количества реализованных единиц - нужно отдельно по каждому виду товара разделить сумму реализации на цену (табл. 6.3.).

Таблица 6.3

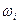
Город	Цена, руб.	Сумма реализации, ты руб.	Частоты
А З0 600 20
Б 20 1 000 50
В 35 350 10

Итого 1950 80

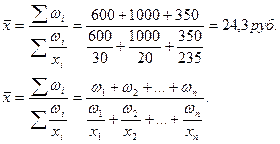
При определении средней цены, используя невзвешенную среднюю арифметическую, получим среднюю, которая не отражает объема реализации, т. е. нереальна.

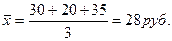
Как видно, средняя гармоническая является превращенной формой арифметической средней. Вместо гармонической всегда можно рассчитать среднюю арифметическую, но для этого сначала нужно определить веса отдельных значений признака.

В том случае, если объемы явлений, т. е. произведения, по каждому признаку равны, применяется средняя гармоническая (простая).

Пример. Две автомашины прошли один и тот же путь: одна со скоростью 60 км/ч, а вторая-80 км/ч, тогда средняя скорость составит:

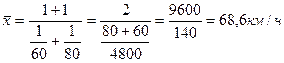
тогда

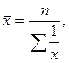
где - сумма обратных значений вариант; n - число вариант.

Дата добавления: 2014-01-11