
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Связь решения дифференциального уравнения 2-го порядка
|
|
|
|
с нахождением минимума квадратичного функционала.
Пусть имеется краевая задача для дифференциального уравнения 2-го порядка:

Покажем, что математически проблема решения краевой задачи для дифференциального уравнения (на примере (1),(2)) эквивалентна задаче вариационного исчисления – о минимуме интеграла, для которого дифференциальное уравнение является уравнением Эйлера-Лагранжа.
Рассмотрим функционал (интеграл)
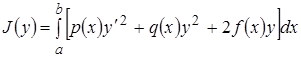 (3)
(3)
Он получит для всякой функции 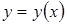 , заданной при
, заданной при 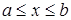 , определенное значение. Таким образом, величина интеграла
, определенное значение. Таким образом, величина интеграла 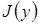 зависит от выбранной кривой, т.е.
зависит от выбранной кривой, т.е. 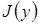 - функционал.
- функционал.
Поставим задачу: найти кривую 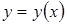 , проходящую через заданные точки (а,А) и (
, проходящую через заданные точки (а,А) и (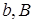 ) и дающую минимальное значение интегралу
) и дающую минимальное значение интегралу 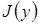 .
.



 Пусть
Пусть 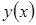 есть функция, дающая интегралу
есть функция, дающая интегралу 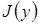 минимальное значение.
минимальное значение.
y Пусть 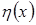 - любая непрерывная
- любая непрерывная
 со своей производной функция и
со своей производной функция и
(b,B) 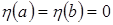 . Тогда
. Тогда 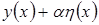

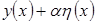

 удовлетворяет граничным условиям (2)
удовлетворяет граничным условиям (2)
и при достаточно малых 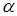 сколь угодно
сколь угодно
 (a,A)
(a,A) 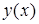 близка к функции
близка к функции 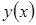 . Так как
. Так как 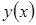
 дает
дает 
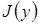 , то при
, то при 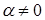 должно
должно
а b x быть 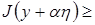
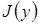 . Интеграл
. Интеграл 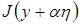 как функция от
как функция от 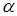 при
при 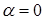 имеет минимум. Поэтому
имеет минимум. Поэтому
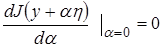 (4)
(4)
(3)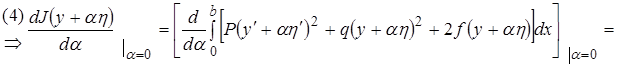
=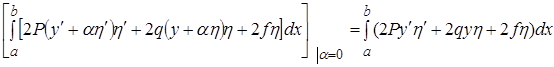 (4¢)
(4¢)
При малых 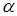
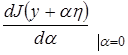 дает главную часть приращения интервала при переходе от кривой
дает главную часть приращения интервала при переходе от кривой 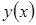 к кривой
к кривой 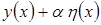 и это выражение называют вариацией интеграла
и это выражение называют вариацией интеграла 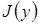 и обозначают
и обозначают 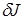 :
:
(5¢) 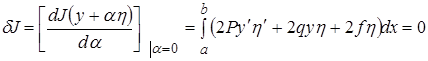 , т.е. вариация
, т.е. вариация
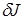 должна быть равной нулю, какова бы ни была
должна быть равной нулю, какова бы ни была 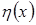 .
.
Преобразуем первое слагаемое, интегрируя по частям:
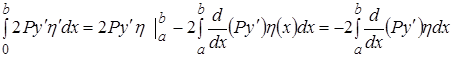 .
.
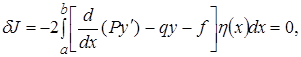 (5)
(5)
которое должно быть равно нулю при любых 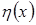 . Это возможно только в том случае, если
. Это возможно только в том случае, если 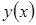 удовлетворяет дифференциальному уравнению
удовлетворяет дифференциальному уравнению
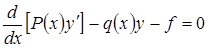 (6)
(6)
Итак, мы установили, что функция 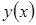 , дающая минимум интегралу
, дающая минимум интегралу
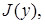 необходимо должно удовлетворять уравнению (6). Значит, решение краевой задачи (1), (2) можно заменить решением вариационной задачи (3),(2).
необходимо должно удовлетворять уравнению (6). Значит, решение краевой задачи (1), (2) можно заменить решением вариационной задачи (3),(2).
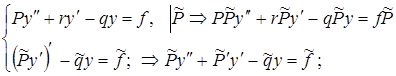
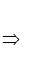
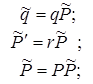
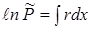
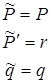
Уравнение, которому удовлетворяют экстремальные кривые, называется уравнением Эйлера-Лагранжа для данной вариационной проблемы. В данном случае это уравнение (6) – самосопряженное дифф. уравнение.
Общее решение (6) содержит в своем составе две произвольные постоянные. Через две точки (а,А) и (в,В) можно, вообще говоря, провести одну кривую, удовлетворяющую уравнению (6). Можно показать, что именно эта кривая представляет решение экстремальной проблемы. Покажем это.
Пусть 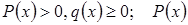 - непрерывно дифференцируемая функция
- непрерывно дифференцируемая функция
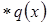 и
и 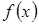 - непрерывны на
- непрерывны на 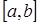 .
.
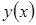 - решение полученное, а
- решение полученное, а 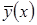 - другая функция, удовлетворяющая
- другая функция, удовлетворяющая
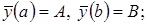 тогда, если
тогда, если 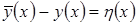 и
и 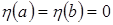 .
.

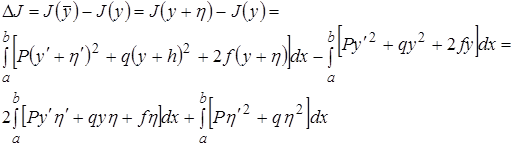 (7)
(7)
Первое слагаемое есть 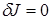 . Второе слагаемое с учетом условий
. Второе слагаемое с учетом условий 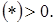 Значит
Значит 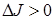
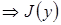 и
и 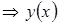 дает интегралу
дает интегралу 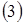 абсолютный экстремум
абсолютный экстремум 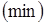 .
.
Замечание. Следует отметить, что всякое линейное дифф. уравнение 2-го порядка является уравнением Эйлера-Лагранжа для некоторого интеграла (функционала) типа (3). Действительно, любое уравнение (1¢)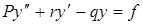 умножением на
умножением на 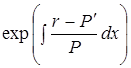 можно
можно
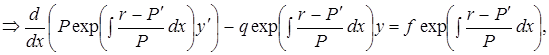 т.е.
т.е.
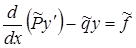 , для которого выполняется (3).
, для которого выполняется (3).
В общем случае для функционала
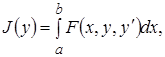 при
при 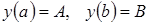 (8)
(8)
Уравнение Эйлера-Лагранжа имеет вид (в классе гладких функций)
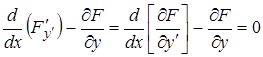 ,
, 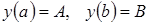 (9)
(9)
Действительно, 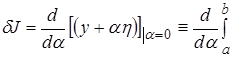
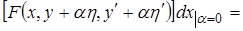
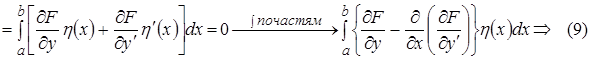
Пример. Уравнение изгиба балки 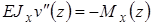 с граничными условиями
с граничными условиями 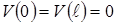 получается как уравнение Эйлера-Лагранжа из функционала:
получается как уравнение Эйлера-Лагранжа из функционала:
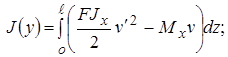
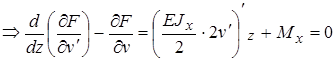 .
.




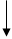
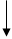

 .
. 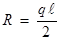 Mx q
Mx q







 z
z















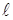
Примечания. 1) Пусть имеется функционал и граничные условия:

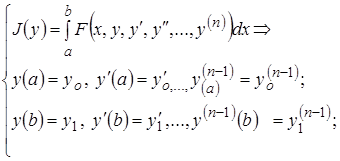
Соответствующее уравнение Эйлера-Лагранжа имеет вид:
(10¢) 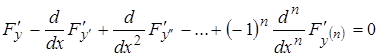 - дифференциальное уравнение 2n порядка.
- дифференциальное уравнение 2n порядка.
2) 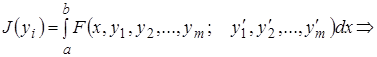 (11)
(11)
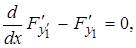 или
или 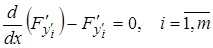 (11¢)
(11¢)
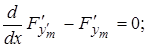
3) 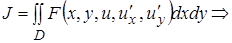 (12)
(12)
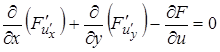 (12¢)
(12¢)
Пример.  функционала
функционала
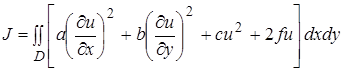 дает
дает
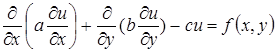
4) Методы решения дифференциальных уравнений путем минимизации функционалов (соответствующих) называют прямыми методами вариацион-ного исчисления. Методы минимизации функционалов путем решения соответствующих уравнений Эйлера-Лагранжа называются непрямымиметодами вариационного исчисления.
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 446; Нарушение авторских прав?; Мы поможем в написании вашей работы!