Естественные краевые условия

Если решение вариационной задачи является пределом последовательности элементов, каждый из которых не удовлетворяет граничным условиям дифф. задачи, то такие граничные условия называются естественными (например, условия Неймана). Если каждый элемент этой последовательности удовлетворяет граничным условиям, то они называются главными (например, условие Дирихле).

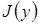Мы рассматриваем задачу о функционала (3) при условиях:

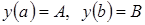, которая эквивалентна задаче (1),(2) (те же граничные условия) Часто приходится иметь дело с дифф. уравнениями с граничными условиями других типов. Выясним: какие вариационные проблемы приводят к ним?

Для этой цели рассмотрим задачу (3) о 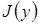, не налагая никаких условий на функцию 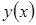или при так называемых естественных условиях. В этом случае ход рассуждений остается прежний, но только нельзя пользоватьсяусловиями 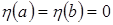. При этом выражение (5¢) для 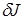сохраняет силу, но при интегрировании по частям уже имеем:

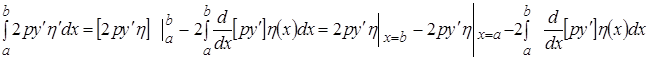Поэтому (5) имеет вид:

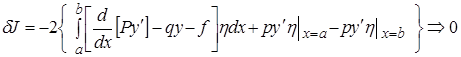(5¢¢)

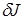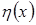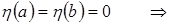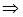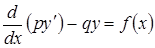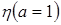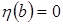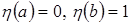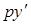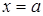Так как должно быть равно нулю для любой функции , в частности, при . Интегральный член должен равняться нулю выполняется (6): . Далее, выбирая и , затем убеждаемся, что при и х=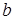должно равняться 0.

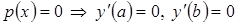(13)

Таким образом, решение задачи об экстремуме функционала (3) при естественных граничных условиях представляет решение уравнения (6) при условиях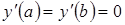

Рассмотрим получение других видов граничных условий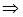

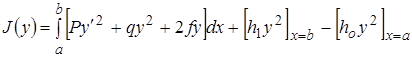(14)

с учетом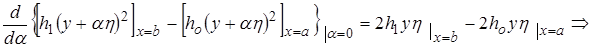

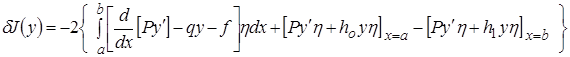(15)

)

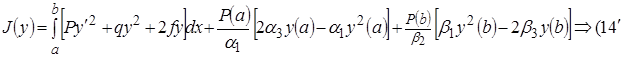Аналогичными рассуждениями получим:

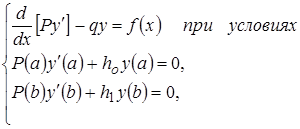(16)

т.е. (14) эквивалентна (16) и наоборот. Здесь уже в (14¢) заложены граничные условия.

(16¢)

Дата добавления: 2014-01-14