Формулы приближенного дифференцирования, основанные на первой интерполяционной формуле Ньютона

Всего надежность и правильность принимаемых решений.

Здоровый образ жизни необходимо рассматривать как основу профилактики заболеваний.

Здоровый образ жизни есть способ жизнедеятельности, соответствующий генетическим особенностям данного человека, конкретным условиям жизни и направленный на формирование, сохранение и укрепление здоровья, на полноценное выполнение человеком его социально-биологических функций. Обязательным является учет индивидуальности каждого человека. В организации здорового образа жизни для конкретного человека необходимо учитывать следующие факторы:

- индивидуальные наследственные особенности человека (морфофункциональный тип, тип высшей нервной деятельности, преобладающий механизм вегетативной нервной регуляции и т.д.);

- природно-экологические и социально-экологические условия среды жизни человека (конкретные условия жизни, в которых осуществляется семейно-бытовая и профессиональная деятельность);

- возрастную и половую принадлежность человека и социально-экономические условия жизни (семейное положение, профессию, традиции, условия труда и быта, материальное обеспечение);

- личностно-мотивационные особенности человека (его жизненные установки и степень их ориентации на здоровье и здоровый образ жизни).

Основными элементами здорового образа жизни каждого человека должны быть: оптимальный двигательный режим, тренировка иммунитета и закаливание, рациональное питание, отсутствие вредных привычек, рациональный режим жизни. Особую важность имеет формирование здорового образа жизни у детей, пока их нервная система более пластична, а жизненные установки еще недостаточно прочны.

Если гигиена исходит из задач общественного здоровья через улучшение качества среды на всех уровнях, то индивидуальное здоровье человека всесторонне рассматривает интенсивно развивающаяся отрасль медицины – валеология. Валеология – теория и практика формирования, сохранения и укрепления здоровья индивида с использованием медицинскихи парамедицинских технологий. Предмет валеологии – индивидуальное здоровье человека,его механизмы. Главным ее объектом является здоровый человек,а основной задачей – разработка и реализация методов и способов, которые позволили бы управлять здоровьем человека таким образом, чтобы он не стал больным, т.е. объектом традиционной медицины.

Пусть на отрезке 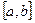заданы равноотстоящие точки 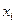: 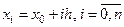, , 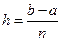и известны значения функции в этих точках 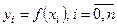. Требуется найти производные 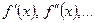на отрезке 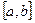(заранее известно, что эти производные существуют).

Заменим функцию 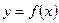интерполяционным полиномом Ньютона, построенным для узлов 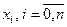, воспользовавшись первой интерполяционной формулой Ньютона:

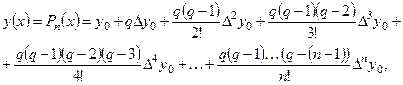(6.1)

где .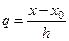

Произведя перемножение биномов и приведя подобные, получим:

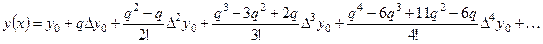(6.2)

Так как

,

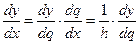то

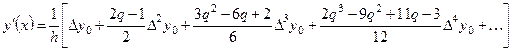(6.3)

Аналогично, так как

,

то

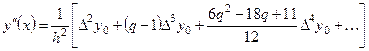. (6.4)

Таким образом можно вычислить производную любого порядка.

При нахождении производных 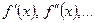в фиксированной точке 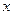в качестве 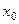следует брать ближайшее к 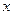табличное значение аргумента.

Формулы (6.3) и (6.4) упрощаются, если нужно подсчитать производные в узлах интерполяции. Полагая 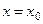, , 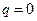получаем:

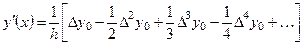, (6.5)

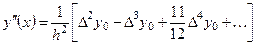. (6.6)

Пусть 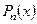- интерполяционный полином Ньютона, содержащий конечные разност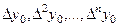и и 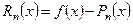, тогда 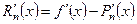. Но 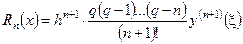. Тогда, если 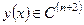, то

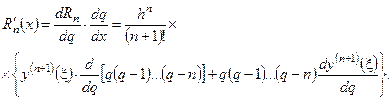(6.7)

Полагая 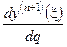- ограниченной и учитывая, что 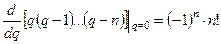, получаем при , :

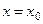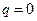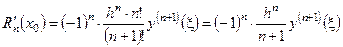. (6.8)

Так как 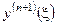сложно определить, то при малом шаге 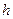принято считать 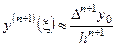. Тогда (6.8) примет вид:

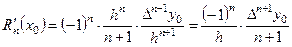. (6.9)

Аналогично находится 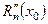и так далее.

Формулы приближенного дифференцирования аналогичным образом можно получить, используя вторую интерполяционную формулу Ньютона.

Дата добавления: 2014-01-14