Теоремы о степенях вершин и изоморфизм графов

Способы задания графов

Рассмотрим три способа задания графов: графический, аналитический и матричный.

1) Графический способ.

Вершины изображают точками на плоскости, а ребра – линиями, соединяющими соответствующие точки. Для изображения дуги используется линия со стрелкой, указывающей направление от начала к концу дуги.

На рисунке 12 изображен смешанный граф с вершинами v ₁, v ₂,¼, v ₆, ребрами e ₁, e ₂, e ₃, e ₅ и дугой e ₄. Смежные вершины v ₁, v ₂, инциденты ребру e ₁. Вершины v ₁, v ₃, инциденты параллельным ребрам e ₂ и e ₃. Вершине v ₄ инциденты петля e ₅ и дуга e ₄, причем v ₄ является началом дуги e ₄, а v ₅ – концом этой дуги. Степень вершины v ₁ равна 3, вершины v ₂ – 1, вершины v ₃ – 2, вершины v ₄ – 3, вершины v ₅ – 1, вершины v ₆ – 0. Таким образом, вершины v ₂ и v ₅ – висячие, а вершина v ₆ – изолированная. В случае дуги e ₄ точнее было бы говорить о полустепенях исхода и захода вершин v ₄ и v ₅, а именно: полустепень исхода вершины v ₄ равна 3, вершины v ₅ – 0, полустепень захода вершины v ₄ равна 2, вершины v ₅ – 1.

2) Аналитический способ.

Граф задают перечислением элементов множества вершин и множества ребер. Для графа, изображенного на рисунке 12, эти множества: V ={ v ₁, v ₂, v ₃, v ₄, v ₅, v ₆} и Е ={ e ₁, e ₂, e ₃, e ₄, e ₅}, где e ₁=(v ₁, v ₂), e ₂=(v ₁, v ₃), e ₃=(v ₁, v ₃), e ₄=(v ₄, v ₅), и e ₅=(v ₄, v ₄).

3) Матричный способ.

Имеется несколько вариантов задать граф матрицей. Наиболее употребимыми являются матрица инциденций и матрица смежности.

а) Матрица инциденций – это прямоугольная матрица, число строк которой равно числу вершин, а число столбцов – числу дуг (ребер) графа. Элементы этой матрицы определяются следующим образом:

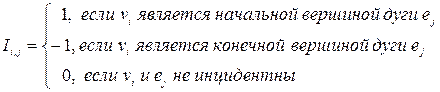
Таким образом, для графа на рисунке 12 матрица инциденций такова:

		e 1	e 2	e 3	e 4	e 5
	v 1
	v 2
I=	v 3
	v 4
	v 5				-1
	v 6

По этой матрице легко судить о наличии в графе параллельных ребер (два одинаковых столбца), петли (одна единица в столбце), дуги (значения разных знаков в столбце), изолированной вершины (нулевая строка), висячих вершин (одно ненулевое значение в строке).

б) Матрица смежности вершин – это квадратная матрица, размер которой определяется числом вершин в графе. Элементы этой матрицы определяются так: . Если в графе имеются параллельные ребра, то соответствующий элемент матрицы смежности полагают равным числу этих ребер. Так матрица смежности для графа на рисунке 12 такова:

		v 1	v 2	v 3	v 4	v 5	v 6
	v 1
	v 2
S=	v 3
	v 4
	v 5
	v 6

По виду этой матрицы также несложно судить о наличии в графе кратных ребер, дуг, петель, висячих и изолированных вершин.

Теорема 1: Сумма степеней вершин в неориентированном графе четна и равна удвоенному числу ребер.

Аналогичная теорема может быть сформулирована и для орграфов: сумма полустепеней исхода всех вершин равна сумме их полустепеней захода и равна числу дуг орграфа.

Теорема 2:Число вершин нечетной степени в любом графе четно.

Два графа G ₁ и G ₂ называются изоморфными, если существует биективное отображение между множествами их вершин и ребер такое, что соответствующие друг другу по этому отображению ребра графов G ₁ и G ₂ инцидентны соответствующим друг другу по этому же отображению парам вершин этих графов.

Согласно определению, графы, изображенные на рисунке 13, изоморфны. Соответствие между множествами вершин и ребер таково:

для вершин: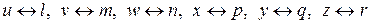

для ребер: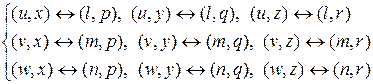

Дата добавления: 2014-01-14