Одиночная шарообразная частица

Однопараметрическая дифференциальная модель (ОДМ)

Идеальное смешение.

Идеальное вытеснение.

Траектории движения частиц в зависимости от структуры потока.

(вихревое движение.)

Участвуют в сложном возвратно-поступательном движении (существует продольное перемешивание).

ЛЕКЦИЯ 15

При материальном описании используют двухуровневую модель:

1) Одиночная шарообразная частица.

2) Модель, описывающая процесс рабочей зоны реактора.

Рассматривается уравнение материального баланса, используемое в дифференциальной форме для элементарного реакционного объёма dV. Составление УМБ для элемента dV, (л 2, стр. 83.)

Требования dV:

Все технологические параметры: (Т, Р, С, U…) выровнены по dV, равны между собой и остаются постоянны за время dτ (лекция 2, стр. 129).

Уравнение материального баланса для dV:

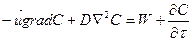(15.1)

где 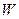– массовая скорость кристаллизации загрязняющего вещества. (см. реакцию 14.1).

Вблизи поверхности твёрдые частицы в пределах гидродинамического пограничного слоя δ (рис. 3.2), продольная скорость жидкости U убывает до 0, причём поперечный конвективный перенос отсутствует.

и массоперенос к поверхности твёрдой частицы определяется главным образам диффузией (в сферических координатах).

Уравнение диффузии записывается в следующем виде:

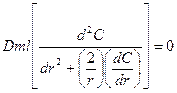(15.2)

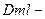коэффициент молекулярной диффузии (), табличная величина.

граничные условия (рис.3.2)

коэффициент загрязнения вещества,

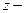продольная координата (рис. 14.2 б)

Решение дифференциального уравнения 15.2 позволяет получить распределение концентрации вблизи твёрдой частицы.

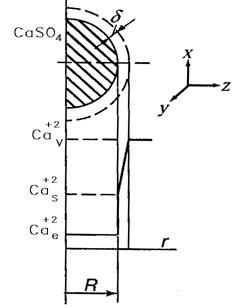
и решений уравнения (15.2)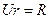

(15.4)

На поверхности твёрдой частицы: протекает реакция.

(14.1) с образованием нерастворимого соединения содержащего , который откладывается в виде отложения на поверхности шарообразной частицы. За счет этих процессов частицы увеличиваются в размере.

С учётом (15.2 и 15.4)

Решение в виде

(15.5)

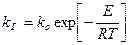– уравнение Аррениуса

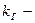константа скорости реакции.

Для уравнения (14.1) реакция I порядка

и массовая скорость кристаллизации

кг (15.7)

критерий Дамкелера. Он характеризует интенсивность, относительность кинетических и внешне диффузионных процессов.

(процессы массопереноса этим распределением).

Уравнение 15.6 и 15.5 – представляет собой математическую модель, составленную для одиночной шарообразной частицы (рис. 14.2 а3), см. затравочные кристаллы.

Дата добавления: 2014-11-06