Основные тождества алгебры множеств

Алгебра множеств. Основные тождества алгебры множеств

Геометрическое моделирование множеств. Диаграммы Венна

Для наглядного представления множеств и отношений между ними используется диаграммы Венна (иногда их называют кругами Эйлера или диаграммами Эйлера – Венна).

Универсальное множество изображают в виде прямоугольника, а множества, входящие в универсальное множество, – в виде кругов внутри прямоугольника; элементу множества соответствует точка внутри круга (рис 1.1а)).

С помощью диаграмм Венна удобно иллюстрировать операции над множествами.

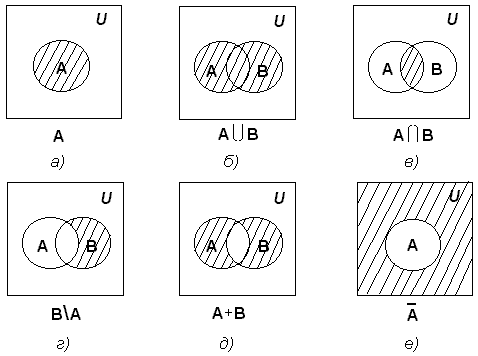
Рис.1.1

Множества вместе с определенными на них операциями образуют алгебру множеств. Последовательность выполнения операций задается с помощью формулы алгебры множеств. Например, Ç (В È C), (А \ В) + C – формулы алгебры множеств.

Для любых множеств A, B, C справедливы следующие тождества:

1. Коммутативность.

а) A È B  = B È A (для объединения);

б) A Ç B = B Ç A (для пересечения).

2. Ассоциативность.

а) A È (B È C) = (A È C) È C (для объединения);

б) A Ç (B Ç C) = (A Ç B) Ç C (для пересечения).

3. Дистрибутивность.

а) A È (B Ç C) = (A È B) Ç (A È C) (для объединения относительно пересечения);

б) A Ç(B È C) = (A Ç B)È(A Ç C) (для пересечения относительно объединения).

4. Закон де Моргана.

а) = Ç (дополнение к объединению есть пересечение дополнений);

б) = È (дополнение к пересечению есть объединение дополнений).

5. Идемпотентность.

а) A È A = A (для объединения);

б) A Ç A = A (для пересечения).

6. Поглощение.

а) A È (A Ç B) = A;

б) A Ç (A È B) = A.

7. Расщепление (склеивание).

а) (A È B) Ç (A È ) = A;

б) (A Ç B) È (A Ç ) = A.

8. Двойное дополнение.

= A.

9. Закон исключенного третьего.

A È = U.

10. Операции с пустым и универсальным множествами.

а) A È U = U;

б) A È Æ = A;

в) A Ç U = A;

г) A Ç Æ = Æ;

д) = U;

е) = Æ.

11. А \ В = A Ç .

Чтобы доказать некоторое тождество A = B, нужно доказать, что, во-первых, если x Î А, то x Î В и, во-вторых, если x Î В, то x Î А. Докажем таким образом, например, свойство дистрибутивности для объединения (тождество 3а)):

A È (B Ç C) = (A È B) Ç (A È C).

1. Сначала предположим, что некоторый элемент x принадлежит левой части тождества, т.е. x Î A È (B Ç C), и докажем, что x принадлежит правой части, т.е. x Î(A È B) Ç (A È C).

Действительно, пусть x Î A È (B Ç C). Тогда либо x Î A, либо x Î B Ç C. Рассмотрим каждую из этих возможностей.

Пусть x Î A. Тогда x Î A È B и x Î A È C (это верно для любых множеств B и C). Следовательно, x Î(A È B) Ç (A È C).

2. Предположим, что некоторый элемент x принадлежит правой части тождества, т.е. x Î (A È B) Ç (A È C), и докажем, что x принадлежит левой части, т.е. x Î A È (B Ç C).

Действительно, пусть x Î (A È B) Ç (A È C). Тогда x Î A È B, и одновременно x Î A È C. Если x Î A È B, то либо x Î A, либо x Î B, если. x Î A È C, то либо x Î A, либо x Î C. Пусть x Î A, Тогда x Î A È (B Ç C) и утверждение доказано. Если x Ï A, то одновременно должны выполняться условия x Î B и x Î C, т.е. x Î B Ç C. Но тогда x Î B Ç C и x Î A È (B Ç C), что также доказывает наше утверждение.

Доказательство тождеств можно проиллюстрировать с помощью диаграмм Венна.

Основные тождества алгебры множеств можно использовать для доказательства других тождеств.

Пример 1.14.

Доказать тождество (A È B) \ В = A Ç .

Преобразуем левую часть тождества, используя тождество 11:

(A È B) \ В = (A È B) Ç .

Затем используем закон дистрибутивности (тождество 3б):

(A È B) Ç = A Ç È B Ç .

Используем закон исключенного третьего (тождество 9):

B Ç = Æ.

Получим

A Ç È B Ç = A Ç È Æ.

Используем свойство пустого множества (тождество 10б):

A Ç È Æ = A Ç .

Тождество доказано.

Пример 1.15.

Доказать тождество:

A \ (В \ C) = (A \ В)È (A Ç C).

Множества, стоящие в левой и правой частях тождества, изобразим с помощью диаграмм Эйлера – Венна (рис. 1.2).

Рис. 1.2

Рис. 1.2 б) и рис. 1.2 д) иллюстрируют равенство множеств A \ (В \ C) и (A \ В)È (A Ç C).

Докажем тождество из нашего примера, воспользовавшись тождествами:

А \ В = A Ç , = È , = A, A Ç(B È C) = (A Ç B)È(A Ç C).

Получим:

A \ (В \ C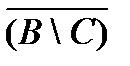) = A Ç = A Ç 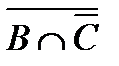= A Ç ( 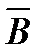È ) = A Ç (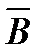 È C) = (A Ç 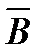) È (A Ç C) = (A \ В)È (A Ç C).

Основные тождества алгебры множеств можно также использовать для упрощения формул алгебры логики.

Пример 1.16.

Упростить выражение:

(A È B) Ç ( È B) Ç (A È ).

Используя закон коммутативности (тождество 1б), поменяем местами вторую и третью скобки:

(A È B) Ç ( È B) Ç (A È ) = (A È B) Ç (A È ) Ç ( È B).

Применим закон расщепления (тождество 7а) для первой и второй скобок:

(A È B) Ç (A È ) Ç ( È B) = A Ç ( È B).

Воспользуемся законом дистрибутивности (тождество 3б):

A Ç ( È B) = A Ç È A Ç B.

Используем закон исключенного третьего (тождество 9):

A Ç = Æ.

Получим

A Ç È A Ç B = Æ È A Ç B.

Используем свойство пустого множества (тождество 10б):

Æ È A Ç B = A Ç B.

Итак,

(A È B) Ç ( È B) Ç (A È ) = A Ç B.

Дата добавления: 2014-11-06