Цифровое представление вещественных чисел

Цифровое представление символов

Правило цифрового представления символов следующее: каждому символу ставится в соответствие некоторое целое число, то есть каждый символ нумеруется.

Пример

Рассмотрим последовательность строчных букв русского алфавита: а, б, в, г, д, е, ё, ж, з, и, й, к, л, м, н, о, п, р, с, т, у, ф, х, ц, ч, ш, щ, ъ, ы, ь, э, ю, я. Присвоив каждой букве номер от 0 до 33, получим простейший способ представления символов. Последнее число - 32 в двоичной форме имеет вид 100000, то есть для хранения символа в памяти понадобится 6 бит. Так как с помощью шести бит можно представить число 2⁶ – 1 = 63, то шести бит будет достаточно для представления 64 букв.

g

Имеются разные стандарты для представления символов, которые отличаются лишь порядком нумерации символов. Наиболее распространён американский стандартный код для информационного обмена - ASCII [American Standard Code for Information Interchange] введён в США в 1963г. В 1977 году в несколько модифицированном виде он был принят в качестве всемирного стандарта Международной организации стандартов [International Standards Organization - ISO] под названием ISO-646. Согласно этому стандарту каждому символу поставлено в соответствие число от 0 до 255. Символы от 0 до 127 – латинские буквы, цифры и знаки препинания – составляют постоянную часть таблицы. Остальные символы используются для представления национальных алфавитов. Конкретный состав этих символов определяется кодовой страницей. В русской версии ОС Windows95 используется кодовая страница 866. В ОС Linux для представления русских букв более употребительна кодировка КОИ-8.

Недостатки такого способа кодировки национального алфавита очевидны. Во-первых, невозможно одновременное представление русских и, например, французских букв. Во-вторых, такая кодировка совершенно непригодна для представления китайских или японских иероглифов. В 1991 году была создана некоммерческая организация Unicode, в которую входят представители ряда фирм (Borland, IBM, Lotus, Microsoft, Novell, Sun, WordPerfect и др.), и которая занимается развитием и внедрением нового стандарта. Кодировка Unicode использует 16 разрядов и может содержать 65536 символов. Это символы большинства народов мира, элементы иероглифов, спецсимволы, 5000 мест для частного использования, резерв из 30000 мест.

Пример

ASCII-код символа A = 65₁₀ = 41₁₆ = 01000111₂;

ASCII-код символа G = 71₁₀ = 47₁₆ = 01000111₂;

ASCII-код символа Z = 90₁₀ = 5A₁₆ = 01011010₂.

ASCII-код символа C = 67₁₀ = 43₁₆ = 01100111₂

Unicode-код символа C = 67₁₀ = 0000000001100111₂.

g

Для того, чтобы представить вещественное число в виде набора целых чисел, его необходимо привести к нормализованной форме:

x = M*2^P;

где M - называется мантиссой (дробной частью), а P - экспонентой (порядком).

После этого мантисса и порядок переводятся в двоичное представление. В памяти ЭВМ вещественное число хранится в виде:

здесь S – признак знака. Поэтому необходимо также определить, какой размер памяти будет отведён под все три части нормализованного числа.

Далее должны быть определены правила (алгоритмы), по которым будут выполняться арифметические операции с нормализованными вещественными числами. Совокупность таких алгоритмов, а также правил представления чисел в нормализованной форме называется арифметикой плавающих чисел [floating point number].

Поскольку размер памяти, отводимый под мантиссу и порядок, ограничен, то вещественные числа представляются с некоторой погрешностью (точность десятичных цифр) и имеют ограниченный диапазон изменения. Чем больше размер памяти для плавающего числа, тем точнее можно представить вещественное число. Поэтому для пользователя основными характеристиками арифметики плавающего числа являются длина числа (размер), измеряемая в битах, и точность представления числа. По точности представления вещественных чисел различают плавающие числа одинарной и двойной точности [single and double precision].

Пример

Рассмотрим принцип цифрового представления вещественного числа 15,375. Пусть под мантиссу отведено 5 десятичных разрядов, а под порядок – 2 разряда. Представим число в нормализованной форме: 15,375» 1,9219*2³. Так как в нормализованной форме первая цифра всегда равна единице, то её можно не хранить. Тогда число будет представлено в виде целого числа 9219003 с относительной погрешностью не более 10^-4, то есть число верных десятичных чисел равно 4. В памяти ЭВМ это число будет храниться в двоичной форме, причём можно легко подсчитать, что для хранения такого числа потребуется 27 бит. Максимальное число, которое можно представить таким образом - 9999999=1,99999*10⁹⁹, а минимальное, не равное нулю - 0000100=0,00001. Если предусмотреть один бит для хранения знака порядка, то минимально представляемое число будет равно 00001-99, то есть 0,00001*10^-99.

При попытке выйти за допустимый диапазон ЭВМ выдаст сообщение о переполнении (underflow или overflow).

g

Конкретные характеристики арифметики различны для разных стандартов. Для ПЭВМ наиболее распространённым является IEEE-стандарт (IEEE-754-1985) [Institute of Electrical and Electronic Engineers], согласно которому вещественные числа представляются в трёх основных формах (см. табл. 1.2).

Таблица 1.2 Данные с плавающей точкой по IEEE-стандарту

Тип	Размер, бит	Диапазон изменения чисел максимум минимум	Точность десятичн. цифр	Машинное e
single		3.4*10^-38	3.4*10^38		1,192*10^-7
double		1.7*10^-308	1.7*10^308		2,221*10^-16
long double		3.4*10^-4932	3.4*10^4932		1,084*10^-19

Здесь нужно заметить, что характеристики плавающего числа двойной точности будут зависеть от той арифметики, которая используется на конкретной ЭВМ.

Пример

Запишем число 15,375 в двоичном виде:

15.375 = 1111.011₂ = 1.111011*2¹¹₂

Тогда согласно стандарту IEEE число будет представляться:

single

15,375 = 0 1000.0001.0 111.0110.0000.0000.0000.0000₂ = 41760000₁₆

long double

15,375 = 0 1000.0000.00010. 1110.1100.0000.0000. … 0000₂ = 402ЕС00000000000₁₆.

Источник: [Ошибка! Источник ссылки не найден.].

g

Особенности плавающей арифметики могут существенно влиять на результаты расчётов, вплоть до того, что погрешность может сделать невозможным получение какого-либо результата вообще, поэтому знание деталей реализации арифметики плавающих чисел является необходимым для программистов.

Пример

Существует особая характеристика плавающей арифметики – машинное эпсилон. Это число, которое определяется как

.

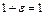Для плавающего числа единичной точности (по IEEE стандарту):

.

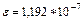Это значит, если написать программу на языке BASIC:

a=1.2

b=1.e-7

print a+b

то результат, который выдаст программа, будет равен 1.2.

Поэтому программы, учитывающие особенности плавающей арифметики могут трактовать все числа, меньшие, чем машинное эпсилон, практически равными нулю.

g

Дата добавления: 2014-11-06