Узагальнений закон Гука

Деформації при об’ємному напруженому стані.

Досліджуючи деформації й розглядаючи питання міцності при об’ємному та плоскому напружених станах, будемо відповідно до основних гіпотез та припущень вважати, що матеріал відповідає закону Гука, а деформації малі.

Відносна поздовжня деформація: (1)

а відносна поперечна деформація: 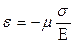(2)

Розглянемо деформацію елемента тіла

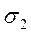
c+Δc b+Δb

с

b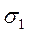

_a

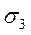
a+Δa

Внаслідок деформації ребра елемента змінюють свою довжину й дорівнюють:

a+Δa; b+Δb; c+Δc.

Величини:

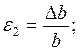
Називаються головними подовженнями і являють собою відносні подовження в головних напрямах.

Застосовуючи принцип суперпозиції, можна записати: 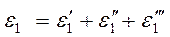, де

- відносне подовження в напружені 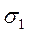, спричинене тільки на 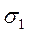при .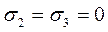

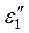- відносне подовження в тому самому напрямі, спричинене дією тільки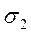

- подовження спричинене дією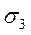

Оскільки напрям 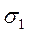самого напруження 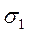є поздовжнім, а для напружень 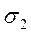та 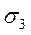– поперечним, то застосовуючи формули (1), (2) знаходимо, що

; ;

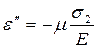Склавши ці величини, матимемо

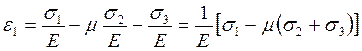
Аналогічно

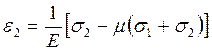
Це узагальнений закон Гука для ізотропного тіла

Для плоского напруженого стану

;

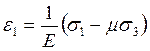
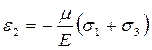
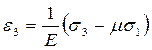
Критерій найбільш нормальних напружень з трьох головних напружень враховує тільки одне – найбільше, вважаючи, що два інших не впливають ні міцність

Недоліки: Ця теорія дає задовільні результати тільки для дуже крихких матеріалів (камінь, цегла, кераміка, інструментальна сталь). Ця теорія не відображує перехід до пластичного стану.

Об’ємна деформація:

Нехай до деформації елемент займав об’єм 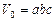. У деформованому стані його об’єм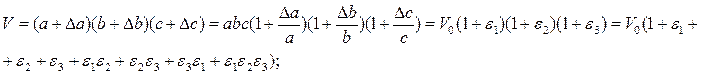

;

Враховуючи узагальнений закон Гука

;

Можна ввести величину 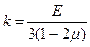- модуль об’ємної деформації.

Потенціальна енергія деформації:

Потенціальною енергією деформації називається енергія, що накопичується в тілі при його пружному деформуванні. Для стержня питома потенціальна енергія, тобто енергія, яка припадає на одиницю об’єму.

;

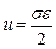враховуючи, що , матимемо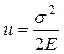

Для об’ємного напруженого стану

;

При деформуванні елемента взагалі змінюється як його об’єм, так і форма(він з кубика перетворюється на паралелепіпед).

;

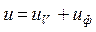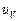- питома потенціальна енергія зміни об’єму

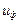- питома потенціальна енергія формозміни, та енергія яка накопичується внаслідок зміни форми елемента.

;

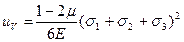Критерії міцності (теорії міцності):

І. Критерій найбільших нормальних напружень.

Припускається, що руйнування матеріалу в загальному випадку напруженого стану виникає тоді, коли найбільше нормальне напруження досягає небезпечного значення . Останнє визначають при простому розтяганні або стисканні зразків з даного матеріалу

;

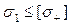; , де ;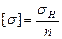

Дата добавления: 2014-11-06