Вопрос 3. Дифракция света на круглом экране и круглом отверстии

Если на пути света от точечного источника S поставить не слишком большой круглый экран 2 так, чтобы перпендикуляр, опущенный на него из источника света, проходил через его центр, то в точке наблюдения Р по-прежнему будет свет, хотя и меньшей интенсивности, рис. 9.2.

Проведя через край экрана 2 линию РN ₀, произведем деление фронта световой волны Ф, начиная от точки N ₀, на такие же зоны Френеля, как и ранее. Повторяя все рассуждения, получим, что для идеального круглого экрана 2, закрывающего (m – 1) первых зон Френеля, результирующая амплитуда колебаний в точке Р будет А ' = А _m¢/2, где А _m¢ - амплитуда первой открытой зоны, отсчитываемой от N ₀. По мере увеличения экрана 2 величина А ' будет убывать, но точка Р остается освещенной всегда практически до тех пор, пока экран не закроет достаточно большое число зон Френеля. Лишь в этом последнем случае станет справедливым положение геометрической оптики о прямолинейном распространении света: препятствие, перекрывающее луч SР, даст в точке наблюдения геометрическую тень. Вблизи границ тени будет наблюдаться слабая дифракционная картина.

Более того, если сделать "зонный экран", состоящий из ряда непрозрачных колец, закрывающих все нечетные (или все четные) зоны Френеля, то результирующая амплитуда

А = А₂ + А ₄ + А ₆.... (9.5)

оказывается даже большей, чем при отсутствии всякого экрана. Т.е. такой экран действует подобно собирательной линзе (рис. 9.3).

Рис. 9.3.

Еще большего эффекта можно достичь, не перекрывая четные (или нечетные) зоны, а изменяя фазу их колебаний на p. Это можно осуществить с помощью прозрачной пластинки, толщина которой в местах, соответствующих четным или нечетным зонам, отличается на определенную величину. Такая пластинка называется фазовой зонной пластинкой. По сравнению с перекрывающей зоны амплитудной зонной пластинкой применениефазовой пластинки даст дополнительное увеличение амплитуда в два раза, а интенсивности света - в 4 раза.

Деление фронта волны Ф на зоны Френеля является относительным и зависит от расстояния до точки наблюдения Р.

Пренебрегать дифракционными явлениями и рассматривать свет распространяющимся прямолинейно вдоль лучей, исходящих от источника, допустимо лишь, если размеры экрана велики по сравнению с размерами зон Френеля. Чем короче l, тем меньше размеры этих зон и тем точнее можно пользоваться приближенными понятиями лучевой (геометрической) оптики. Т.к. для видимого света l = 0,4 - 0,8 мкм, то при наблюдении макроскопических тел этими приближениями можно пользоваться с достаточной точностью. Однако при уменьшении размеров тел начинают проявляться дифракционные явления.

Поставим на пути сферической световой волны распространяющейся от источника света S непрозрачный экран D с вырезанным в нем круглым отверстием радиуса r ₀ (рис.9.4). Расположим экран так, чтобы перпендикуляр, опущенный из источника света S, попадал в центр

отверстия O. На продолжении этого перпендикуляра возьмем точку P, в которую поместим экран E, параллельный плоскости отверстия.

Рис.9.4

Если расстояния а и b удовлетворяют соотношению (9.1), где m - целое число, то отверстие оставит открытым ровно m первых зон Френеля, построенных для точки О. Из (9.1) число открытых зон Френеля определяется выражением

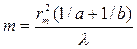. (9.6)

В соответствии с (9.3) амплитуда результирующего колебания в точке Р будет равна

А = А₁ - А ₂ + А ₃ – А ₄ +....± А _m. (9.7)

Перед А _m берется знак «+», если m нечетное, и минус, если m - четное. Представив (9.7) в виде, аналогичном (9.4), и положив выражения в скобках равными нулю, получим

А = А ₁/2 + А _m /2 (m - нечетное), (9.8)

А = А ₁/2 + А _m-1/2 – А _m (m - четное).

Амплитуды от двух соседних зон практически одинаковы. Поэтому

(А _m-1/2) – А_m можно заменить через - А _m/2. В результате получится:

А = А ₁/2 ± А_m /2, (9.9)

где знак «+» берется для нечетных значений m и минус - для четных.

Для малых m амплитуда А _m мало отличается от А ₁. Следовательно, при нечетных m амплитуда в точке Р будет приблизительно равна а ₁, при четных m – нулю, рис.9.4.

А какая будет освещенность в других точках экрана? Вследствие симметричного расположения отверстия относительно прямой SР освещенность в разных точках экрана будет зависеть только от расстояния х от точки Р. Если смещаться по экрану в точку Р ¢ и далее, то дифракционная картина будет иметь вид чередующихся светлых и темных концентрических колец. Изменение освещенности экрана в зависимости от расстояния от точки Р показано на рис.9.4. Если отверстие открывает лишь часть центральной зоны Френеля, на экране получается размытое светлое пятно; чередования светлых и темных колец в этом случае не возникает.

Аналогичная картина на экране получается и в рассмотренном выше случае, когда между источником света и экраном помещается непрозрачный круглый диск с радиусом r ₀ (рис.9.5).

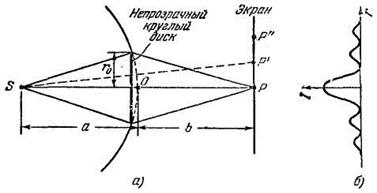
Рис.9.5

Дифракционная картина на экране будет иметь вид чередующихся светлых и темных концентрических колец. В центре картины наблюдается светлое пятно.

Подобным образом можно рассматривать дифракцию Френеля от прямолинейного края полуплоскости и дифракцию от бесконечной щели.

Дата добавления: 2014-11-06