Лабораторна робота №7 1 страница

Тема. Табличний процесор MS Excel. Автоматизація рішення задач економічного планування за допомогою надбудови «Поиск решения»

Мета роботи: навчитися проводити розрахунки у табличному процесорі MS Excel за допомогою надбудови «Поиск решения».

Автоматизація рішення задач економічного планування за допомогою надбудови «Поиск решения» у середовищі Microsoft Excel.

Для реалізації оптимізаційних задач планування економічних процесів в Microsoft Excel існує надбудова «Поиск решения».

«Поиск решения» доставляє не заздалегідь відомий конкретний результат для цільової функції, а відшукує оптимальне (мінімальне або максимальне) з можливих рішення. Для складних задач «Поиск решения» може генерувати множину різних рішень. Шаблон задач планування економічних процесів, для рішення яких можна скористатися надбудовою, повинен мати ряд загальних властивостей:

1. Існує єдина цільова чарунка, що містить формулу.

2. Формула в цільовій чарунці містить посилання (прямі або непрямі) на ряд змінюваних чарунків.

Може бути задана деяка кількість обмежень.

Приклад 1. Задача оптимізації використання ресурсів (задача планування виробництва).

Для виготовлення двох видів продукції P₁ і P₂ використовують чотири види ресурсів S₁, S₂, S₃, S₄. Запаси ресурсів, число одиниць ресурсів, затрачуваних на виготовлення одиниці продукції, наведені в табл. 1 (цифри умовні).

Таблиця 1 – Умовні дані задачі оптимізації ресурсів

Вид ресурсу	Запас ресурсу	Число одиниць ресурсів, затрачуваних на виготовлення одиниці продукції
P1	P2
S1
S2
S3		-
S4			-

Ціна реалізації одиниці продукції P₁ і P₂ відповідно, становить 2 і 3 грн.

Необхідно скласти такий план виробництва продукції, при якому прибуток від реалізації буде максимальним.

Методичні вказівки

Складемо оптимізаційну модель задачі.

Позначимо:

x₁, x₂ – число одиниць продукції відповідно P₁ і P₂, запланованих до виробництва.

Для їхнього виготовлення (табл. 1) буде потрібно (1* x₁+3* x₂) одиниць ресурсу S₁, (2* x₁+1* x₂) одиниць ресурсу S₂, (1* x₂) одиниць ресурсу S₃, (3* x₁) одиниць ресурсу S₄. У наслідок того, що споживання ресурсів S₁, S₂, S₃, S₄ не мусить перевищувати їхніх запасів, відповідно 18, 16, 5 і 21 одиниць, то зв'язок між споживанням ресурсів і їхніх запасів виражається системою обмежень:

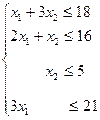
Змінні позитивні x₁³0, x₂³0.

Сумарний прибуток F від реалізації продукції складе:

.

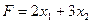Прокоментуємо рішення задачі оптимізації використання ресурсів підприємства. Першою дією необхідно ввести вхідні дані. Уведемо на робочий аркуш вхідну таблицю з даними як це показано на рис.1.

Для формування обмежень задачі в чарунку Е5 уводимо функцію:

СУММПРОИЗВ (C10:D10;C5:D5).

Виклик функції здійснюється наступними командами:

Вставка – Функция – Математические – СУММПРОИЗВ - Массив 1 (C10:D10) (невідомі значення плану виробництва) – Массив 2 (C5:D5) (ресурси одиниці продуцкії). Копіюємо функцію у чарунки С6:С8 за допомогою маркеру заповнення.

У чарунку С11 уводимо цільову функцію:

СУММПРОИЗВ (C10:D10;C9:D9).

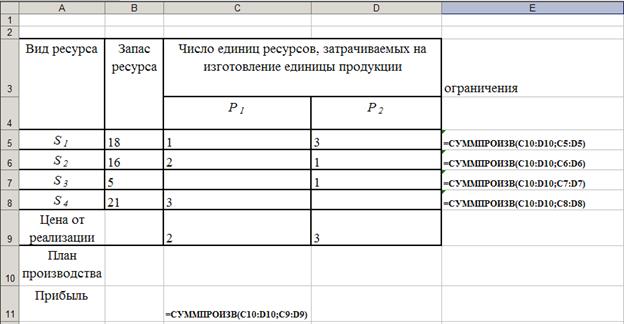
Рисунок. 1 – Шаблон рішення задачі оптимізації використання ресурсів

Перейдемо тепер до постановки задачі для надбудови «Поиск решения» середовищі MS Excel.

Для розв'язуваної задачі цільовою функцією буде функція у чарунці $С$11, змінюваними даними - діапазон $С$10:$D$10, що містить число видів продукції, діапазон $Е$5:$Е$8 - використовується для визначення обмежень задачі.

Для звертання до надбудови «Поиск решения» використовується команда меню Сервис. Але може бути так, що команда Поиск решения в цьому меню відсутня. Тоді необхідно виконати наступну команду: Сервис / Надстройки, навпроти Поиск решения поставити галочку. Після активації команди Поиск решения, необхідно заповнити вікно діалогу за зразком (рис.2).

Установити цільову чарунку $С$11, що дорівнює максимальному значенню. Змінюючи чарунки $С$10:$D$10. Для ведення обмежень потрібно натиснути на кнопку Добавить.

1. Обмеження по ресурсах:

Посилання на чарунки: $Е$5:$Е$8, вид обмеження: <=, Обмеження: посилання на чарунки: $В$5: $В$8. Добавить.

2. Обмеження на не заперечність змінних:

Посилання на чарунки: $С$10:$D$10, вид обмеження: >=, Обмеження 0. Добавить.

3. Обмеження на цілісність змінних:

Посилання на чарунки: $С$10:$D$10, вид обмеження: цел. OК.

Рисунок. 2 Вікно діалогу «Поиск решения»

Після натискання по кнопці Выполнить надбудова «Поиск решения» приступає до ітерацій, після обчислень відкриває діалогове вікно Результаты поиска решения (рис.3), у якому виводиться повідомлення про рішення задачі.

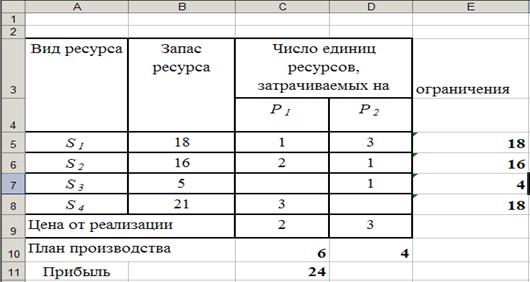
Рисунок. 3 Результати рішення задачі оптимізації використання ресурсів

У результаті рішення задачі можна зробити наступний висновок. Максимальний прибуток становитиме 24, продукції типу P₁ необхідно виробляти 6, продукції типу P₂ – 4.

Приклад 2. Задача оптимізації складання раціону (задача про дієту, задача про суміші).

Є два види корму I і II, що містять живильні речовини (вітаміни) S₁, S₂, S₃. Кількість одиниць живильних речовин в 1 кг кожного виду корму, необхідний мінімум живильних речовин наведені в табл. 2 (цифри умовні).

Таблиця 2 – Умовні дані задачі оптимізації складання раціону

Живильна речовина (вітаміни)	Необхідний мінімум живильних речовин	Число одиниць живильних речовин в 1 кг корми
I	II
S1
S2
S3

Вартість 1 кг корму I і II відповідно дорівнює 4 і 6 грн.

Необхідно скласти денний раціон, що має мінімальну вартість, у якому зміст кожного виду живильних речовин було б не менш установленої межі.

Складемо оптимізаційну модель задачі.

Позначимо:

x₁, x₂ – кількість кормів I і II, що входять у денний раціон.

Тоді цей раціон буде включати (3* x₁+1* x₂) одиниць живильної речовини S₁, (1* x₁+2* x₂) одиниць речовин S₂, (1* x₁+6* x₂) одиниць живильної речовини S₃. У наслідок того, що кількість живильних речовин S₁, S₂, S₃ у раціоні мусить бути не менш, відповідно 9, 8 і 12 одиниць, то маємо систему обмежень:

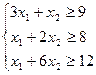, (1)

Змінні позитивні x₁³0, x₂³0.

Загальна вартість раціону F складе:

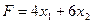. (2)

Перейдемо тепер до постановки задачі для надбудови «Поиск решения» середовищі MS Excel.

Прокоментуємо рішення задачі складання раціону. Першою дією необхідно ввести вхідні дані. Уведемо на робочий аркуш вхідну таблицю з даними як це показано на рис.4.

Для формування обмежень задачі в чарунку F4 уводимо функцію:

СУММПРОИЗВ (D4:E4;$D$8:$E$8).

У чарунку D9 уводимо цільову функцію:

СУММПРОИЗВ (D7:E7;D8:E8).

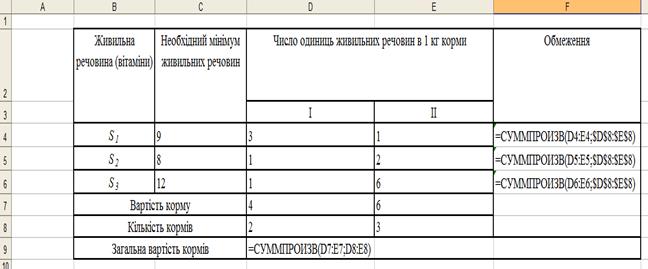
Рисунок 4 - Шаблон рішення задачі складання раціону

Виклик надбудови «Поиск решения» (рис.5.)

Установити цільову чарунку $D$9, що дорівнює мінімальному значенню. Змінюючи чарунки $D$8:$E$8. Для ведення обмежень потрібно натиснути на кнопку Добавить.

1. Обмеження по ресурсах:

Посилання на чарунки: $C$4:$C$6, вид обмеження: <=, Обмеження: посилання на чарунки: $F$4: $F$6. Добавить.

2. Обмеження на не заперечність змінних:

Посилання на чарунки: $D$8:$E$8, вид обмеження: >=, Обмеження 0. Добавить.

3. Обмеження на цілісність змінних:

Посилання на чарунки: $D$8:$E$8, вид обмеження: цел. OК.

Рисунок. 5 Вікно діалогу «Поиск решения»

На рис.6. наведено результати вирішення задачі складання раціону. Мінімальна загальна вартість кормів складає – 26, першого виду корму необхідно виробляти 2 кг., а другого – 3 кг.

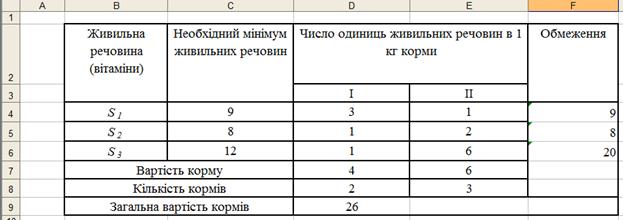
Рисунок. 6 Результати рішення задачі складання раціону

Приклад 3. Задача оптимізації транспортних витрат.

Є три постачальники та чотири споживачі. Потужність постачальників і попит споживачів, а також витрати на перевезення одиниці вантажу для кожної пари «постачальник - споживач» зведені в таблицю постачань (таблиця3).

Таблиця 3 – Таблиця постачань

Постачальники	Потужності постачальників	Споживачі і їхній попит

У лівому верхньому куті довільної (i,j) клітки є коефіцієнт витрат – витрати на перевезення одиниці вантажу від i -го постачальника до j-го споживача.

Задача формулюється в такий спосіб: знайти обсяги перевезень для кожної пари «постачальник - споживач» так, щоб потужності всіх постачальників були реалізовані, попити всіх споживачів були задоволені, сумарні витрати на перевезення були б мінімальні.

Позначимо через x_ij обсяг перевезення від i -го постачальника до j - го споживача. Задані потужності постачальників і попити споживачів накладають обмеження на значення невідомих x_ij. Щоб потужність кожного з постачальників була реалізована, необхідно скласти рівняння балансу для кожного рядка таблиці постачань:

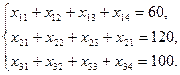
Аналогічно, щоб попит кожного зі споживачів був задоволений, подібні рівняння балансу складаються для кожного стовпця таблиці поставок:

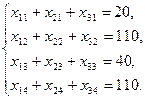
Очевидно, що обсяг перевезеного вантажу не може бути негативним, тому варто ввести обмеження не заперечності змінних:

x_ij ≥0.

Сумарні витрати F на перевезення виражаються через коефіцієнти витрат у такий спосіб:

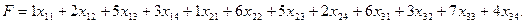
Перейдемо тепер до постановки задачі для надбудови «Поиск решения» середовищі MS Excel.

Прокоментуємо рішення задачі оптимізації транспортних витрат. Представимо дані для рішення задачі в матричній формі. Формується матриця 3:4. Шаблон подання даних для реалізації задачі представлений на рис. 7.

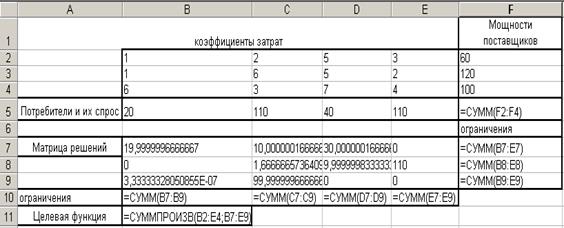
Рисунок. 7 - Шаблон з вхідними даними для рішення задачі оптимізації транспортних витрат

Уводимо в діапазон B2:E4 коефіцієнти витрат на перевезення, у діапазон B5:E5 уводимо потреби у вантажах, у діапазон F2:F4 уводимо потужності постачальників.

У чарунку F5 для перевірки типу транспортної задачі уводимо формулу:

=СУММ(F2:F4)

Якщо задача закрита, то сума потужностей постачальників дорівнює сумі попиту споживачів. Якщо балансу не дотримується, то необхідно додати фіктивного постачальника або споживача, як коефіцієнти витрат у доданому стовпці або рядка вводиться значення - 0.

Для формування шаблона рішення задачі необхідно ввести наступні розрахункові формули.

Уводимо у чарунку В10 формулу =СУММ(В7:В9), у чарунки C10:E10 копіюємо дану формулу методом протягання (у такий спосіб сформоване обмеження з попиту споживачів).

Уводимо у чарунку F7 формулу =СУММ(B7:E7), у чарунки F8:F9 копіюємо дану формулу методом протягання (у такий спосіб сформоване обмеження по потужностям постачальників).

Уводимо у чарунку В11 формулу для розрахунку значення цільової функції:

=СУММПРОИЗВ(В2:Е4;В7:Е9).

Далі звертаємося до надбудови «Поиск решения». Заповнюємо вікно діалогу як показане на рис. 8.

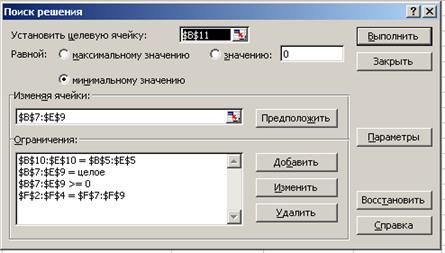
Рисунок. 8 - Вікно діалогу «Поиск решения»

Установлюємо цільову чарунку $B$11, що дорівнює мінімальному значенню. Змінюючи чарунки $B$7:$E$9. Далі уводимо обмеження, за допомогою кнопки Добавить.

1. Обмеження з попиту:

Посилання на чарунку: =$B$10:$E$10, вид обмеження: =, Обмеження $B$5:$E$5. Добавить.

2. Обмеження на цілісність змінних:

Посилання на чарунку: =$B$7:$E$9, вид обмеження: = цілий. Добавить.

3. Обмеження на не заперечність змінних:

Посилання на чарунку: =$B$7:$E$7, вид обмеження: >=, Обмеження 0. Добавить.

4. Обмеження по потужностях постачальників:

Посилання на чарунку: =$F$2:$F$4, вид обмеження: >=, Обмеження $F$7:$F$9. ОК.

Оптимальне рішення отримано після натискання по кнопиці Виполнить. На рис. 7 у діапазоні B7:E9 зазначений оптимальний розподіл перевезень вантажів для кожної пари «постачальник - споживач».

Індивідуальні завдання для лабораторної роботи №7

Варіант №1

Задача 1

При складанні добового раціону годування скота можна використовувати свіже сіно (не більше 50 кг) та силос (не більше 85 кг). Раціон повинен мати число кормових одиниць не менше ніж 30 і споживчі елементи: білок (не менше ніж 1 кг), кальцій (не менше ніж 100 г) і фосфор (не менш ніж 80 г). В таблиці наведено дані про концентрацію необхідних елементів в 1 кг кожного корму і собівартості (коп./кг) цих кормів. Необхідно скласти добовий раціон годування скота, що має мінімальну вартість.

Таблиця

Види кормів	Концентрація споживчих елементів в кормах	Собівартість кормів, коп./кг
Кількість кормових одиниць, кг	Білок, г/кг	Кальцій, г/кг	Фосфор, г/кг
Сіно свіже	0,5		1,25
Силос	0,5		2,5

Задача 2

Є чотири постачальники й чотири споживачі. Потужність постачальників і попит споживачів, а також витрати на перевезення одиниці вантажу для кожної пари «постачальник - споживач» зведені в таблицю поставок. Необхідно знайти обсяги перевезень для кожної пари «постачальник споживач» так, щоб сумарні витрати на перевезення були б мінімальні.

Таблиця

Постачальники	Потужності постачальників	Споживачі і їхній попит

Варіант №2

Задача 1

Для виготовлення чотирьох видів продукції використовують три види сировини. Запаси сировини, норми його витрат й прибуток від реалізації кожного продукту наведені в таблиці. Скласти математичну модель на максимум загальної вартості продукції, що випускається.

Таблиця

Вид сировини	Норми витрат сировини на 1 виріб, кг	Запаси сировини, кг
А	Б	В	Г
Прибуток від реалізації 1 виробу, грн

Задача 2

Є чотири постачальники й п'ять споживачів. Потужність постачальників і попит споживачів, а також витрати на перевезення одиниці вантажу для кожної пари «постачальник - споживач» зведені в таблицю поставок. Необхідно знайти обсяги перевезень для кожної пари «постачальник споживач» так, щоб сумарні витрати на перевезення були б мінімальні.

Таблиця

Постачальники	Потужності постачальників	Споживачі і їхній попит

Варіант 3

Задача 1

На підприємстві випускаються три види виробів, при цьому використовуються три види сировини. Запаси сировини, норми його витрат й прибуток від реалізації кожного продукту наведені в таблиці. Скласти математичну модель на максимум загальної вартості продукції, що випускається.

Таблиця

Вид сировини	Норми витрат сировини на 1 виріб, кг	Запаси сировини, кг
Прибуток від реалізації 1 виробу, грн

Задача 2

Є п'ять постачальників і п'ять споживачів. Потужність постачальників і попит споживачів, а також витрати на перевезення одиниці вантажу для кожної пари «постачальник - споживач» зведені в таблицю поставок. Необхідно знайти обсяги перевезень для кожної пари «постачальник споживач» так, щоб сумарні витрати на перевезення були б мінімальні.

Таблиця

Постачальники	Потужності постачальників	Споживачі і їхній попит

Варіант №4

Задача 1

Для виготовлення трьох видів продукції використовують чотири види сировини. Запаси ресурсів, норми їх витрат й ціна від реалізації кожного продукту наведені в таблиці. Скласти математичну модель на максимум загальної вартості продукції, що випускається.

Таблиця

Ресурси	Норми витрат ресурсів на одиницю продукції	Запаси
Праця
Сировина 1
Сировина 2
Устаткування
Ціна

Задача 2

Є п'ять постачальників і п'ять споживачів. Потужність постачальників і попит споживачів, а також витрати на перевезення одиниці вантажу для кожної пари «постачальник - споживач» зведені в таблицю поставок. Необхідно знайти обсяги перевезень для кожної пари «постачальник споживач» так, щоб сумарні витрати на перевезення були б мінімальні.

Таблиця

Постачальники	Потужності постачальників	Споживачі і їхній попит

Варіант 5

Задача 1

Раціон для харчування тварин на фермі складається із двох видів кормів I і II. Кілограм корму I коштує 80 грн. і містить: 1 од. жирів, 3 од. білків, 1 од вуглеводів. Кілограм корму II коштує 10 грн. і містить: 3 од. жирів, 1 од. білків, 8 од вуглеводів. Скласти найбільш дешевий раціон харчування, що забезпечує жирами не менш 6 од., білками не менш 9 од., вуглеводами не менш 8 од. Дані зведені в таблицю.

Таблиця

Живильна речовина	Число одиниць живильних речовин в 1 кг корму	Необхідний мінімум живильних речовин
I	II
Жир
Білок
Вуглевод
Вартість 1 кг корму, грн

Задача 2

Є чотири постачальники й чотири споживачі. Потужність постачальників і попит споживачів, а також витрати на перевезення одиниці вантажу для кожної пари «постачальник - споживач» зведені в таблицю поставок. Необхідно знайти обсяги перевезень для кожної пари «постачальник - споживач» так, щоб сумарні витрати на перевезення були б мінімальні.

Таблиця

Постачальники	Потужності постачальників	Споживачі і їхній попит

Варіант №6

Задача 1

Потрібно скласти суміш, що містить три хімічних речовини А, В, С. Відомо, що складена суміш повинна містити речовини А не менш 6 од., речовини В не менш 8 од., речовини З не менш 12 од. Речовини А, В, З утримуються в трьох видах продуктів - I, II, III, у концентрації, зазначеної в таблиці. Скласти математичну модель, що відповідає мінімальної вартості суміші.

Таблиця

Хімічні речовини	Продукти	Необхідний мінімум хімічних речовин
I	II	III
А
В			1,5
С
Ціна 1 од. продукту, $			2,5

Задача 2

Чотири склади забезпечують товаром три магазини. В таблиці приведені транспортні витрати на доставку одиниці товару від кожного складу до кожного магазину. Необхідно знайти обсяги перевезень для кожної пари «склад-магазин» так, щоб сумарні витрати на перевезення були б мінімальні.

Таблиця

Склади	Магазини	Пропозиція
Попит

Варіант 7

Задача 1

Сільськогосподарське підприємство купує три різних види зерна й виготовлює з них різні види сумішей. Кожний вид зерна містить чотири інгредієнти. Відповідні дані наведені в таблиці. Скласти математичну модель, що відповідає мінімальної вартості суміші.

Дата добавления: 2014-11-06