КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Измерение коэффициента диффузии паров легко испаряющейся жидкости в воздухе
|
|
|
|
Если в некотором объеме имеется неоднородная смесь газов (при одинаковых по всему объему давлении и температуре), то тепловое движение перемешивает их, пока повсюду не образуется однородная смесь молекул, в которой
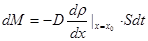где 
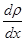- градиент плотности при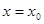 
D - коэффициент диффузии, который численно равен количеству вещества, переносимого через единичную площадку за единицу времени при единичном градиенте плотности.
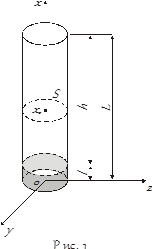
В общем случае D зависит от концентрации газов, однако при малой концентрации одного из газов, коэффициент диффузии можно считать постоянным, т.е. независи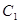
. Для определения коэффициента диффузии паров жидкости в воздухе при малых концентрациях паров применяется следующий метод: жидкость наливается на дно длинной узкой ампулки, укрепленной на чашке магнитных весов. Испаряющиеся с поверхности молекулы жидкости диффузионным путем (если отсутствует перемешивание газа) удаляются из ампулки. Будем исходить из предположения, что над поверхностью жидкости находится насыщенный пар. У краев ампулки концентрация молекул равна нулю.
Чем выше ампулка, тем вероятнее первое предположение. При большой высоте h градиент плотности паров мал. В связи с этим диффузионный поток невелик, то есть сравнительно мало молекул пара отводится путем диффузии от поверхности жидкости. В результате процесс испарения будет успевать поставлять в пар столько молекул, что над поверхностью жидкости будет насыщенный пар. Давление его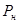 
соответствует температуре Т, при которой проводится эксперимент, и определяется по графику зависимости 
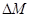от времени t, зависимость, которая при установившемся процессе в координатах 
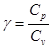- называется коэффициентом Пуассона.
Экспериментальное устройство состоит из стеклянного баллона А, соединенного с жидкостным манометром М и насосом (см. рисунок).
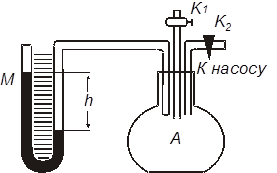Посредством крана К1 система может быть изолирована от атмосферы. Пусть в системе первоначально было Рa – атмосферное давление. В баллон А накачивают небольшое количество воздуха и закрывают кран К2. При плохом обмене теплом с окружающей средой температура воздуха в баллоне несколько повышается. Через некоторое время 
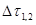воздух в баллоне принимает температуру окружающей среды. При этом разность уровней в манометре становится h1. Это состояние воздуха назовем первым. Его параметры:
· давление -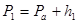 
· удельный объем - 
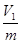· температура – Т1
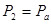· удельный объем - 
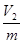· температура - 
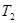Переход от первого состояния ко второму описывается уравнением Пуассона:
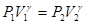(1)
или
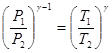(2)
Как только давление в системе станет равным атмосферному, кран К1 закрывают. После этого, охладившийся при расширении воздух за время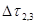 
нагревается до температуры окружающей среды и давление возрастает.
Параметры третьего состояния:
· давление -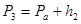 
· удельный объем - 
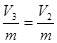· температура - 
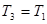Второе и третье состояния связаны уравнением изохоры:
(3)
из (2) и (3) получаем:
.
Содержание
1. Определение коэффициента поверхностного натяжения при помощи горизонтального капилляра..............................3
2. Определение коэффициента поверхностного натяжения по поднятию жидкости в капиллярах………………………5
3. Определение коэффициента поверхностного натяжения жидкости по методу открывания кольца…………………...7
4. Изучение зависимости коэффициента поверхностного натяжения от температуры по методу максимального давления в пузырьке………………………...…………………...9
5. Определение коэффициента внутреннего трения методом Стокса…………………………………………………..12
6. Определение зависимости коэффициента вязкости жидкости от температуры посредствам капиллярного вискозиметра…………………………………………………………16
7. Определение зависимости коэффициента вязкости от температуры………………………………………………...20
8. Определение длинны свободного пробега и эффективного диаметр молекул газа по коэффициенту внутреннего трения………………………………………………………..21
9. Определение молекулярного веса легко испаряющейся жидкости…………………………………………………….24
10. Определение теплоты парообразования легко летучей жидкости по зависимости давления насыщенных паров от температуры………………………………………………...27
11. Изучение законов броуновского движения, и определения размеров взвешенных частиц…………………………30
12. Изучение двумерного распределения Максвелла...….35
(4)
или
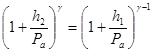(5)
Разложив это выражение по формуле бинома Ньютона и ограничившись членами первого порядка, получим:
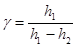(6)
Выполнение работы
1. Определяют времена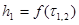 
(7)
Кратковременным поворотом крана К1 систему соединяют с атмосферой. Кран К1 закрывают, когда уровни жидкости в манометре станут одинаковыми.
Строят график
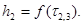(8)
2. Из графиков (7) и (8) определяют времена 
.
Включают нагреватель и операцию «3» повторяют через интервал температуры 9-12 градусов, повышая температуру до 110-120 градусов Цельсия. Во время каждых измерений, температуру воздуха в трубе поддерживают по возможности постоянной. Для этого в электрическую цепь нагревателя вводят реостат. Так как во время опыта температура будет немного меняться, ее измеряют в начале и в конце опыта и берут среднее значение.
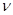(Гц)
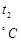
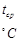
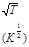
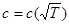, где T – температура взята по шкале Кельвина.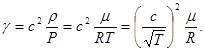
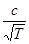берут из графика 
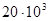герц. Скорость распространения звуковой волны зависит от свойств газа.
Рассмотрим возникновение импульса сжатия в газе. Представим себе пластинку небольших размеров, помещенную в газ. Сообщив пластине быстрое перемещение параллельно ее плоскости, мы вызовем в прилегающем слое газа сжатие и, вследствие этого, фронт повышенного давления. Это давление вызовет движение следующего слоя и так далее. Сжатие и движение будут передаваться от слоя к слою. В газе, вправо от пластины, будет распространяться продольный импульс сжатия. Распространение импульса обусловлено наличием упругих сил, возникающих в газе. Газы обладают упругостью лишь в отношении объема и не обладают упругостью в отношении сдвига. Поэтому в газе будут распространяться только продольные импульсы. Скорость распространения продольного импульса в газе можно рассчитать. Пусть импульс сжатия соответствует увеличению плотности на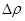 
и увеличению давления на 
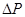. Через площадку S, перпендикулярную к направлению распространения импульса, за время 
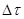проходит часть импульса сжатия 
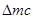, где c – скорость распространения импульса (рис.1).
рис.2
Звуковой сигнал генератора вызывает колебания мембраны телефона (6) и подается на осциллограф. Расстояние между телефоном и микрофоном можно изменять посредством рукоятки (8). При этом указатель рукоятки передвигается вдоль шкалы линейки (9).
Выполнение работы.
1. Осторожно открывают водяной кран, питающий охлаждение телефона (5). (На рисунке не показан).
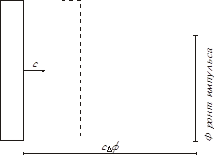рис.1
Масса газа, расположенного справа от площадки S, возрастает на величину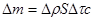 
. При этом через площадку передается импульс 
.
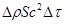Вместе с тем, слева на площадку действует сила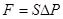 
,
так как
,
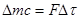то
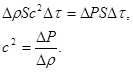(1)
Скорость перемещения импульса сжатия определяется тем, как изменяется плотность среды при изменении давления. Упругие свойства газа зависят от температуры. При быстром сжатии газа выделяется тепло, которое не успевает распространиться на соседние объемы. Сжатие газа без отвода тепла называется адиабатическим. Адиабатический процесс в газе описывается уравнением Пуассона, а именно:
где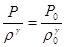 
. (2)
Дифференцируя выражение (2), находим:
.
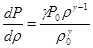В случае малых сжатий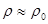 
то:
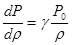. (3)
При этом скорость распространения импульсов сжатия (см. (1) и (3))
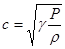. (4)
Из уравнения Менделеева-Клапейрона 
следует, что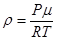 
и соотношение (4) можно представить так:
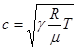. (5)
Значит скорость распространения импульса сжатия (звука) растет пропорционально корню квадратному из температуры.
Звуковые волны можно рассматривать как ряд малых импульсов сжатия, следующих вплотную друг за другом и распространяющихся с одинаковой скоростью. Пусть звук распространяется в трубе, диаметр которой меньше длины волны, но все же не слишком тонкой и обладающей гладкими стенками. При этих условиях стенки не вносят значительного затухания. Они обеспечивают распространение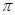
(скорость изменит знак на обратный).
При наложении отраженной волны на бегущую может образоваться стоячая волна с распределением смещений y:
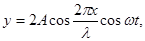(6)
где
A – амплитуда,
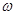- круговая частота колебаний,
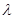- длина бегущей волны,
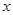- координата, определяющая положение
точек среды,
t – время.
Если при отражении не происходит потерь энергии, на закрытом конце трубы всегда образуется узел смещений. Расстояние между соседними узлами или пучностями равно половине длины бегущей волны. Меняя частоту возбуждения, мы будем получать в закрытой трубе стоячие волны всякий раз, когда вдоль трубы будет укладываться целое число полуволн. Скорость звука определится по формуле:
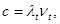(7)
где