
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Расчет переходного режима
|
|
|
|
Расчет производится для послекоммутационной схемы (рис. 3) с учетом независимых начальных условий.
3.1. Записываем искомую величину в переходном режиме в виде суммы установившейся и свободной составляющих, которые соответственно являются частным решением неоднородного дифференциального уравнения и общего решения однородного дифференциального уравнения для искомой величины; i2=i2у+iсв=1+i2св
3.2. Определяем вид свободной составляющей
 Вид свободной
Вид свободной
cоставляющей определяется корнями характеристического уравнения, описывающего искомую величину.
 Составим и решим
Составим и решим
характеристическое
уравнение, для чего наиболее
удобно использовать метод
Zвх(р)=0, где Zвх(р) -
операторное входное
сопротивление, определенное для схемы свободных токов.
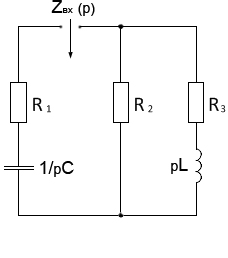
Построив схему свободных токов (рис. 4) иразомкнув какую либо ветвь (например, ветвь 1), найдем входное сопротивление Z вх {р) относительно полюсов разрыва и приравняем его нулю. Удобнее размыкать ветвь, содержащую емкость. На схеме рис 4 емкости соответствует операторноесопротивление 1/рС, а индуктивности - операторное сопротивление pL.

Характеристическое уравнение получим, приравняв нулю числитель выражения для Z вх(р):
 .
.
Подставив в это уравнение числовые значения (R в Омах, С в Фарадах, L в Генри), получаем
33,28-10-6р2 + 1333∙10-3 р + 100=0.
Корни характеристического уравнения равны: p1= -1000 с-1, р2=-3000с-1.
Заметим, что значения корней всегда должны быть отрицательными. Так как получены действительные и различные корни, то
i2=1+  ,(1)
,(1)
где А1 и А2 - постоянные интегрирования, которые необходимо найти, используя независимые начальные условия uс(0-) и iз(0-).
3.3. Определение постоянных интегрирования.
Для определения постоянных интегрирования необходимо иметь столько уравнений, сколько корней у характеристического уравнения. Так как в рассматриваемом примере корней два. то необходимо иметь систему двух уравнений, где неизвестными являются постоянные интегрирования А1 и А2. Недостающие уравнения получают последовательным дифференцированием по времени уравнения, полученного для искомой величины:
i2′= 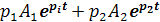 . (2)
. (2)
Подставив в уравнения (1) и (2) t=0, получим

|
(3)
Подставив в систему уравнений (3) значения р1=-1000 с-1 и
р2 = -3000 С-1 получим
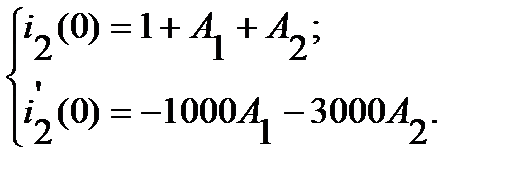
|
(4)
Чтобы найти значения искомой величины и ее производных при t=0, необходимо составить систему уравнений Кирхгофа, для послекоммутационной цепи, затем последовательно ее продифференцировать по времени столько раз, сколько постоянных интегрирования минус 1 и подставить в полученные системы уравнений t=0.
В рассмотренном примере систему уравнений Кирхгофа необходимо дифференцировать один раз, так как постоянных интегрирования две. Выбрав направление обхода контуров цепи рис. 3, получим:
 (5)
(5)
Подставляем в (5) момент времени t=0
 (6)
(6)
Подставляем в (6) числовые значения сопротивлений, ЭДС и величины uc(0)= uc(0-)25В, i3(0)=iз(0-)=0,5А, полученные с использованием законов коммутации:
 (7)
(7)
Решив систему (8), находим:
i1(0) = 0,333 А, i2 (0) = 0,833A, иL (0) = 33,35. (8)
С учетом известных соотношений 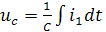 и
и  можно
можно
определить uс и i3 при t=0, которые будут использованы в дальнейших расчетах:
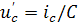 ,
,  (0)/C=0.333/8.6∙10-6=38720 В/с;
(0)/C=0.333/8.6∙10-6=38720 В/с;
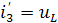 /L;
/L; 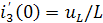 =33.35/25.8∙10-3=1292 А/с.
=33.35/25.8∙10-3=1292 А/с.
Далее подставляем в (6) момент времени t=0:
 (9)
(9)
Подставляем в (9) числовые значения сопротивлений и величины uс'(0) = 38720 В/с, i3(0)= 1292 А/с:
 (10)
(10)
 (10.1)
(10.1)
Решив систему (10), находим требуемую величину i'2(0)=603 А/с. Подставляем найденные i2(0)=0,833 А и i'2(0)=603 А/с в систему уравнений (4) и находим постоянные интегрирования А1 и А2:
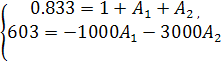 (11)
(11)
А, =0,051; А2 = -0,218.
Следовательно, решение задачи будет иметь вид:
 (11.1)
(11.1)
Следует заметить, что процесс решения задачи сокращается, если необходимо определить переходные ток в индуктивности или напряжение на конденсаторе. В этом случае систему уравнений Кирхгофа не придется дифференцировать. Напряжение на сопротивлении следует искать как произведение R∙i, определив для этого ток i, который по нему протекает.
ПРИМЕР 2
В задаче примера 1 найти напряжение uL если R1 = 0.
1.РАСЧЕТ ДОКОММУТАЦИОННОГО РЕЖИМА. Так как в этом режиме ток i1(0-)=0, величина сопротивления R1 не влияет на uс(0-) и i3(0-) и они будут иметь те же значения, что и в примере 1, то есть uс(0-):=25 В; i3(0-)=0,5 А.
2.РАСЧЕТ УСТАНОВИВШЕГОСЯ РЕЖИМА.
Так как в цепи действует источник постоянной ЭДС, то uLy= 0.
3.РАСЧЕТ ПЕРЕХОДНОГО РЕЖИМА.
uL=uLy+uLсв=0+ uLсв = uLсв.
Подставив значение R1 = 0 в характеристическое уравнение,
составленное в примере 1, получим
LCR2р2+(СR2R3+L)р+R2+Rз = 0.
Подставив в это уравнение числовые значения, получаем
25.8∙10-3∙8.6∙10-6∙50p2+(8.6∙10-6∙50∙50+25.8∙10-3)p+50+50=0,
11.094∙10-6p2+47.3∙10-3p+100=0.
Корни этого характеристического уравнения равны
 .
.
При комплексно сопряженных корнях решение и его производная имеют вид:
 (12)
(12)
 (13)
(13)
В уравнении (12) А и 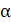 являются постоянными интегрирования. Подставив в уравнение (12)и(13) 1=0, получим
являются постоянными интегрирования. Подставив в уравнение (12)и(13) 1=0, получим
 (14)
(14)
Для определения uL(0) и uL’(0) аналогично примеру 1 составим систему уравнений Кирхгофа, а затем продифференцируем ее по времени:
 (15)
(15)
 (16)
(16)
Подставляем в (15) момент времени t=0:
 (17)
(17)
Подставляем в (17) числовые значения сопротивлений, ЭДС и величины uс(0)=25В, i3(0)=0,5, полученные с использованием законов коммутации:
 (18)
(18)
Решив систему (18), находим: i2(0)=1,5 А, i1(0)=1 А, uL(0)=0.
С учетом соотношений и'с (0) = 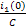 и i3 (0) =
и i3 (0) =  находим:
находим:
ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">  ,
,
 =0/25.8∙10-3=0 A/c.
=0/25.8∙10-3=0 A/c.
Далее подставляем в (16) момент времени t=0:
 (19)
(19)
Решив систему (19), находим требуемую величину uL'(0)=116279 В/с. Подставив найденные uL′(0)=0 и uL′(0)=116279 в систему уравнений (14), находим постоянные интегрирования А и α
 (20)
(20)
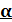 =0; А=55.
=0; А=55.
Решение задачи имеет вид:
 (21)
(21)
Полученное решение для напряжения uL представляет собой затухающую синусоиду.
ПРИМЕР 3
В задаче примера 1 найти ток i1, если e=141∙sin(1000t+30°) В, размыкание ключа Кл1 происходит в момент времени t=0.
1. РАСЧЁТ ДОКОММУТАЦИОННОГО РЕЖИМА
Расчёт цепи рис. 2 произведём с применением комплексного метода. Применим метод двух узлов:
XL=ωL=1000∙25.5∙0.001=25.8 Ом,
Xc=1/ωC=1/(100∙8.6∙10-6)=116 Ом.
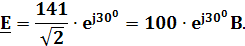
Рассчитаем комплексные сопротивления и проводимости всех ветвей цепи
рис.2.
 Ом
Ом
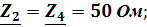
 Ом.
Ом.


 См;
См;

 В
В



Мгновенные значения uc(0-) и i3(0-) равны:
uc(0-)=25∙√2∙sin(1000t-8˚) B,
i3(0-)=0,59∙√2∙sin(1000t+6˚)A.
Получаем независимые начальные условия:
Uc(0)=25 ∙ √2 ∙ sin(-8˚)= -5 B,
I3(0)=0,59 ∙ √2 ∙ sin6˚=0,09 A.
2. РАСЧЕТ УСТАНОВИВШЕГОСЯ РЕЖИМА.
Расчет цепи рис.3 произведем с помощью комплексного метода по аналогии с расчетом докоммутационного режима.




i1y=0,327 ∙ √2 ∙ sin(1000t+83˚)=0,46 ∙ sin(1000t+83˚)A.
3. РАСЧЕТ ПЕРЕХОДНОГО РЕЖИМА.
i1 =i1y+i1cв =0,46 ∙ sin(1000t+83˚) +i1cв
Характеристическое уравнение и его корни получаются такими же, как и в примере №1, так как в схему для свободных токов источник ЭДС не входит: p1=-1000c-1, р2=-3000c-1.

Подставив в эту систему уравнений t=0, получим:
 (22)
(22)
Определяем постоянные интегрирования А1 и А2. Составляем систему уравнений по законам Кирхгофа для цепи рис.3
 (23)
(23)
Подставляем в (23) момент времени t=0:
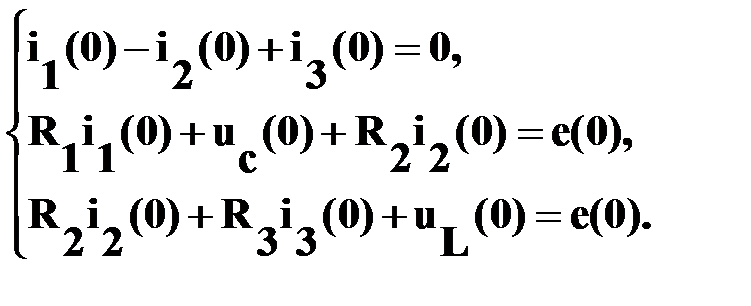 (24)
(24)
e(0)=141∙sin30˚=70,5B, uc(0)=-5B, i3(0)=0,09 A:
 (25)
(25)
Решив систему (25), находим: i1(0)=0,47A,
i2(0)=0,56А; uL(0)=42,5B.
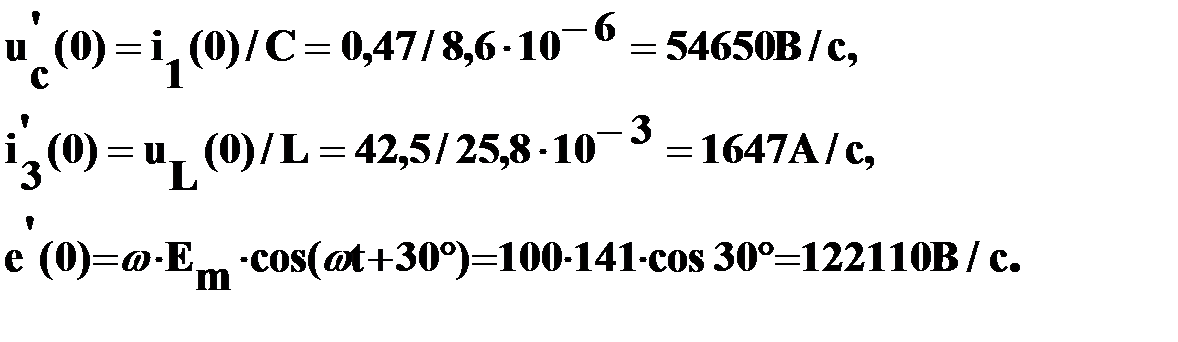
Продифферинцируем по времени систему уравнений (23):
 (26)
(26)
Подствляем в систему уравнений (26) момент времени t=0, числовые значения сопротивлений, 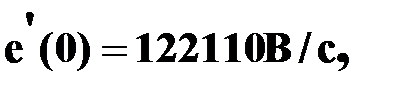



 (27)
(27)
Решив систему (27), находим  .
.
Подставляем полученные значения 
 в систему уравнений (22):
в систему уравнений (22):
 (28’)
(28’)
 (28)
(28)
Решив систему уравнений (28), находим:
А1= -0,0585; А2=0,0715.
Решение задачи имеет вид:

Следует заметить, что при действии в цепи источника синусоидальной ЭДС переходный процесс существенно зависит от момента коммутации.
Библиографический список:
1. Основы теории цепей. Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов.- М.: Энергия, 1985.- 752 с.
2. Бессонов Л.А. Теоретические основы электротехники. Электрические цепи, Iч.-М.: Высш. Школа,1984.-558с.
Рассмотрено на заседании кафедры ЭТЭО
Протокол №______ от ”____”__________2010г.
Заведующий кафедрой
________________________Б.В.Сухинин.
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 478; Нарушение авторских прав?; Мы поможем в написании вашей работы!