Основы биометрической обработки данных

В современной биологии очень трудно указать раздел, в котором не использовались математические методы. Во многом успехи, достигнутые биологией, связаны с планированием эксперимента и использованием методов статистической обработки полученных данных, т. е. с использованием биометрии. Статистический анализ данных, полученных в результате экспериментов и наблюдений, является обязательным компонентом любого научного исследования. С помощью биометрии можно сделать обоснованные выводы о процессах, протекающих в живой природе, проверить достоверность гипотез, выявить биологические закономерности. Данные, не обработанные математически, в большинстве случаев не имеют научной ценности и практической значимости. Более того, игнорирование возможностей статистической обработки полученных данных может привести к ошибочным заключениям. В тоже время ошибки, связанные с методологией или регистрацией данных, нельзя исправить математическими методами. Поэтому начинать работу следует с планирования эксперимента и учета полученных данных.

Формы учета результатов наблюдений. Результаты наблюдений фиксируют в дневниках, журналах, бланках, анкетах и других документах учета. Выбор конкретной формы определяется задачей исследования. Например, на маршрутных зоологических и ботанических экскурсиях удобной формой учета служит дневник. При проведении эксперимента в лабораторных условиях данные фиксируют в протоколах испытаний, журналах, учетных бланках и других формулярах.

Точность измерений. Практически каждый признак имеет свою точность измерения. Например, удой коровы учитывают с точностью до десятых, а при определении полулетальной дозы действия яда необходима точность до тысячных и миллионных долей единицы. Но все же чаще всего измерения проводят с точностью до десятых, сотых или тысячных долей единицы. Более точные измерения проводят реже.

Округление чисел. Числа округляют следующим образом: если за последней сохраняемой цифрой следуют цифры 0, 1, 2, 3, 4, то они отбрасываются (округление с недостатком). Если за последней сохраняемой цифрой следуют цифры 5, 6, 7, 8 и 9, то последняя сохраняемая цифра увеличивается на единицу (округление с избытком). Для более точного округления существуетправило: если за последней сохраняемой цифрой следует цифра 5, то округление осуществляется с недостатком при условии, что сохраняемая цифра четная. Если же сохраняемая цифра нечетная,то округление осуществляется с избытком. Например, числа 3,585 и 3,575 округляются до двух десятичных знаков следующим образом: 3,58 и 3,58.

Группировка первичных данных. Внесенные в документы учета данные об объекте (результаты экспериментов или наблюдений) представляют первичный материал, нуждающийся в соответствующей обработке. Обработка начинается с упорядочения или систематизации собранных данных.

Обработка данных в статистических пакетах. Обработку полученных данных можно провести как в пакетах общего назначения, так и в специализированных пакетах. Наиболее популярным пакетом общего назначения является электронная таблица Excel, из специализированных пакетов специалисты предпочитают программу Statistica. Например, для выполнения статистического анализа в программе Excel необходимо войти в программу. После ввода данных в таблицу в меню Сервис нужно выбрать команду Анализ данных. Если эта команда недоступна, необходимо загрузить пакет анализа. Затем следует выбрать нужную функцию в диалоговом окне Анализ данных (например, Описательная статистика) и провести вычисления. В результате обработки данных в функции описательная статистика мы получаем результаты в виде:

Столбец1
Среднее	8,375
Стандартная ошибка	0,340771
Медиана	8,1
Мода	7,7
Стандартное отклонение	1,363085
Дисперсия выборки	1,858
Эксцесс	4,419741
Асимметричность	1,835846
Интервал	5,6
Минимум	6,8
Максимум	12,4
Сумма
Счет
Уровень надежности(95,0%)	0,726337

Полученные в результате обработки значения биометрических характеристик необходимо проанализировать. Для этого необходимо знать основы биометрии. Ниже приведены некоторые биометрические показатели, которые наиболее часто используются при обработке и интерпретации полученных результатов по биологии.

Средняя. Выделяют несколько видов средних. Однако при обработке биологических данных обычно используют среднюю арифметическую. Эта характеристика отражает целую группу одним (средним) числом и позволяет отличить один групповой объект от другого. Ее обозначают теми же буквами латинского алфавита, что и варианты, но над буквой, соответствующей средней величине, ставят черту. Например, если признак обозначается через x, то средняя арифметическая – 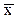. Иногда среднюю арифметическую обозначают буквой M.Определение средней арифметической проводится по формуле:

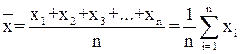
где x_i – значения вариант;

n – общее число вариант или объем данной совокупности;

Σ – знак суммирования.

Кроме средней арифметической используют другие характеристики, определяющие положение центра распределения данных. К ним относятся: медиана Ме – число, разделяющее упорядоченный (по возрастанию или убыванию) ряд экспериментальных данных на две равные части; мода Мо – значение признака, встречающегося в наблюдении наиболее часто. Медиана и мода являются вспомогательными характеристиками наблюдений и используются редко.

Средняя арифметическая, медиана и мода являются наиболее информативными характеристиками распределения, но они не дают полной картины изменчивости признака. Для выявления диапазона рассеяния найденных значений признака обычно используют среднее квадратическое отклонение или стандартное отклонение и коэффициент вариации.

Среднее квадратическое отклонение (S) или стандартное отклонение. Этот показатель характеризует степень рассеяния полученных данных относительно средней. Его определяют по формуле:

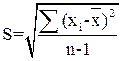
где S– среднее квадратическое отклонение;

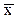– среднее арифметическое;

x_i –значения вариант;

n – общее число вариант (объем данной совокупности).

Ошибка репрезентативности. Ошибку репрезентативности имеют все статистические параметры, рассчитанные по выборке: средняя, стандартное отклонение, коэффициент вариации и др. В практике биологии обычно используют ошибку средней арифметической, которую вычисляют на основе стандартного отклонения. Ошибка средней арифметической – величина отклонения выборочного показателя от средней арифметической – определяется по формуле:

где 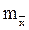– ошибка средней арифметической;

S– среднее квадратическое отклонение;

n – общее число вариант (объем данной совокупности).

Эту формулу используют при n больше 30. Как следует из формулы: с увеличением объема выборки стандартная ошибка среднего арифметического снижается.

Коэффициент вариации. С помощью стандартного отклонения можно сравнить характер варьирования одних и тех же признаков. Для сравнения изменчивости различных признаков, выраженных в различных единицах измерения, используют коэффициент вариации (С_V). Его также обозначают символом V и (СV). Коэффициент вариации вычисляют по формуле:

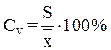
где С_V – коэффициент вариации;

S – стандартное отклонение выборки;

x –средняя арифметическая.

Как свидетельствует практический опыт, для многих биологических признаков наблюдается увеличение стандартного отклонения с ростом их величины (средней арифметической). При этом коэффициент вариации остается примерно на одном и том же уровне 8–15%. За увеличение коэффициента вариации ответственны, как правило, растущие отличия распределения признака от нормального закона.

Коэффициент корреляции. Связь между переменными величинами X и Y можно определить при соотношении числовых значений одной из них с соответствующими значениями другой. Если при увеличении одной переменной увеличивается другая, это свидетельствует о положительной связи между этими величинами. Если при увеличении одной переменной другая переменная уменьшается, это указывает на отрицательную связь. Зависимость между переменными, которым соответствуют средние величины, называется корреляционной, или просто корреляцией. Таким образом, коэффициент корреляции может варьировать в пределах от –1 до +1. Значение коэффициента корреляции до 0,30 свидетельствует о слабой связи, от 0,31 до 0,50 – об умеренной, от 0,51 до 0,70 – о значительной, от 0,71 до 0,90 – о сильной; от 0,91 до 0,99 – об очень сильной.

Коэффициент корреляции обозначается буквой r и определяется по формуле:

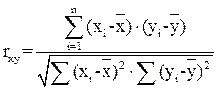
где r_xy – коэффициент корреляции;

x_i и y_i – изучаемые параметры;

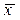и y – средние значения изучаемых параметров.

Доверительный интервал для генеральной средней. Вероятности, достаточные для уверенного суждения о генеральных параметрах на основании выборочных характеристик, называют доверительными. Это понятиепредложено Р. Фишером. В качестве доверительных вероятностей обычно используют вероятности P₁ = 0,95; P₂ = 0,99 и Р₃ = 0,999 (их принято выражать в процентах – 95%, 99%, 99,9%). Это означает, что при оценке генеральных параметров по известным выборочным показателям существует риск ошибиться в первом случае один раз на 20 испытаний, во втором – один раз на 100 испытаний и в третьем – один раз на 1000 испытаний. Выбор порога доверительной вероятности исследователь осуществляет исходя из меры ответственности, с какой делаются выводы о генеральных параметрах. Чем выше мера ответственности, тем более высокий уровень доверительной вероятности используют – 99,0% или 99,9%. Доверительная вероятность 0,95 (95%) считается достаточной в научных исследованиях по биологии.

С доверительной вероятностью тесно связан уровень значимости α, выражают как разность α = 1 – Р. В соответствии с принятыми доверительными вероятностями, α₁ = (1 – 0,95) = 0,05; α₂ = (1 – 0,99) = 0,01; α₃ = (1 – 0,999) = 0,001.

Критерии значимости и проверка гипотез. В исследовательской работе крайне важно установить наличие или отсутствие различий в полученных числовых характеристиках опытной и контрольной групп.

Например, перед исследователем стоит задача сравнить продуктивность нового сорта томата со стандартом (контрольный сорт) в почвенно-климатических условиях юго-востока Белорусского Полесья. После того как по стандартным методикам проведен опыт, оказалась, что средняя урожайность нового сорта превзошла урожайность стандарта. Перед исследователем встает вопрос: можно ли утверждать, что урожайность нового сорта действительно выше урожайности стандарта или это случайность?

Отвечая на этот вопрос, исследователь перед проведением опыта формулирует гипотезы:

1) Нулевая гипотеза (Но) – предполагается, что между урожайностью нового сорта и стандарта разницы нет, а имеющиеся отличия связаны только с действием случайных факторов.

2) Альтернативная гипотеза (Hi) – урожайность нового сорта достоверно превосходит урожайность стандарта.

Далее необходимо доказать действительно ли достоверна, или, наоборот, недостоверна разница в урожайности сравниваемых сортов, т. е. математически подтвердить либо первую либо вторую теорию. В этом контексте термин «достоверно» означает «статистически доказано».
Для этого вычисляют значение некоторой величины, называемой критерием. Найденная величина сравнивается с критическим (граничным) значением критерия, взятым из соответствующих таблиц (приложение М). По результатам сравнения определяется достоверность наличия или отсутствия различий между двумя сравниваемыми параметрами.

Eсли рассчитанное значение критерия t не превосходит критического значения t табличное на уровне значимости α = 0,05, то различия считаются статистически недостоверными, записывается как P > 0,05.

Если вычисленное значение критерия t превышает критические значения t табличное при α = 0,05; α = 0,01 или α = 0,001, то наблюдаемые различия статистически достоверны на уровнях значимости – 0,05; 0,01 или 0,001. Запись производят как P < 0,05, P < 0,01, P < 0,001 соответственно.

Дата добавления: 2014-11-06