
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Коло, його частини. Основні гіпотези науки про опір матеріалів
|
|
|
|
2.
Основні гіпотези науки про опір матеріалів
1. Гіпотеза про суцільність матеріалу. Припускається, що матеріал суцільно заповнює форму тіла.
2. Гіпотеза про однорідність та ізотропність. Матеріал вважається однорідним та ізотропним, тобто в будь-якому об'ємі та в будь-якому напрямі властивості матеріалу вважаються однаковими.
3. Гіпотеза про малість деформації. Припускається, що деформації малі порівняно з розмірами тіла.
4. Гіпотеза про ідеальну пружність матеріалу. Припускається, що всі тіла абсолютно пружні.
Зовнішні і внутрішні сили. Метод перерізів.
Зовнішніми силами називають сили взаємодії між розглядаємим елементом конструкції та пов'язаними з ним тілом.
Зосереджена сила
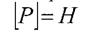
|
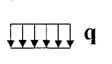 Рівномірно розподілене навантаження
Рівномірно розподілене навантаження
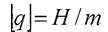 |
Рівнодійна розподіленого навантаження чисельно рівна площі його епюри і прикладена в центрі її ваги.
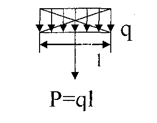
3. Зосереджений момент
 | 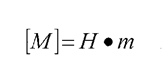 | ||
4. Крутний момент
 [Мкр]= кН •т
[Мкр]= кН •т
Бувають навантаження, які не є наслідком контакту двох тіл наприклад сила інерції, власна вага. Ці сили прикладені в кожній точці об'єму, які займає тіло і тому називаються об'ємними або масовими.
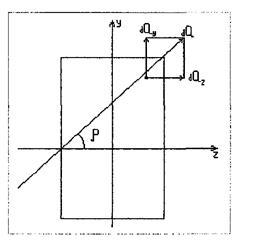
Внутрішні сили
Між сусідніми частинами тіла завжди є певні сили взаємодії, тобто внутрішні сили, які в усіх випадках намагаються зберегти тіло як єдине ціле, протидіють зовнішнім силам, що прикладені до тіла. Внутрішні сили часто називають зусиллям. Для виявлення внутрішніх сил в опорі матеріалів широко застосовують метод перерізів.
Розглянемо довільне тіло
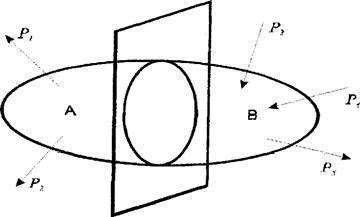
Проведемо переріз
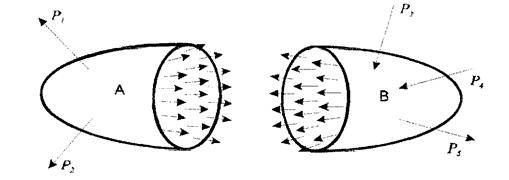
Внутрішні сили можна звести до однієї точки (як правило це центр ваги перерізу), внаслідок чого маємо головний вектор та головний момент внутрішніх сил
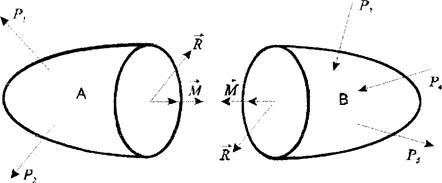
Якщо головний вектор  та головний момент М спроекціювати на осі
та головний момент М спроекціювати на осі 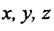 то на кожному боці маємо шість внутрішніх силових факторів:
то на кожному боці маємо шість внутрішніх силових факторів:
три сили 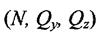 та три моменти
та три моменти 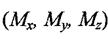 . Ці
. Ці
величини називають внутрішніми зусиллями стержня в перерізі стержня.
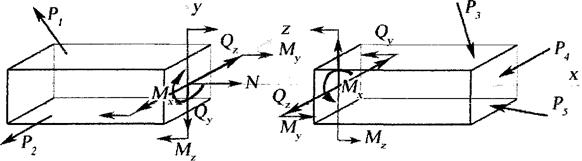
Зусилля N спричиняє поздовжню деформацію стержня
(розтягання або стискання) і зветься поздовжня сила.
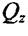
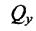 та спричиняє зсув боків перерізу відповідно в напрямку
та спричиняє зсув боків перерізу відповідно в напрямку
осей 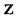 та у, вони звуться поперечні сили або перерізуючи сили.
та у, вони звуться поперечні сили або перерізуючи сили.
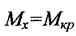 спричинює кручення перерізу зветься крутний момент
спричинює кручення перерізу зветься крутний момент
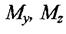 спричинюють згин, звуться згинальні моменти
спричинюють згин, звуться згинальні моменти
Напруження в перерізі
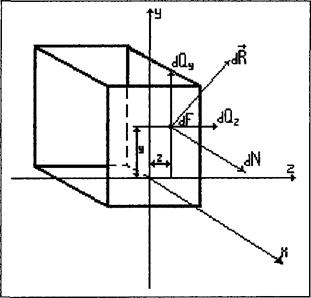 Розглянемо нескінченно малий елемент площі
Розглянемо нескінченно малий елемент площі 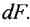 Унаслідок малості елемента можна вважати, що внутрішні зусилля, які діють в його різних точках, однакові за модулем та напрямом. Тоді їхня рівнодійна
Унаслідок малості елемента можна вважати, що внутрішні зусилля, які діють в його різних точках, однакові за модулем та напрямом. Тоді їхня рівнодійна 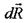 буде проходити через центр ваги елемента
буде проходити через центр ваги елемента 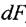 ', координати якого
', координати якого 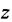 та
та 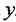 .
.
Отже, зводячи все до центра ваги елемента
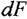 , матимемо головний вектор
, матимемо головний вектор 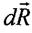 та
та
головний момент 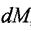 , що дорівнює 0
, що дорівнює 0
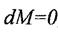 , т.к. центр ваги тоді:
, т.к. центр ваги тоді:
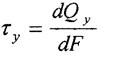
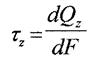
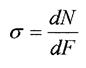
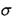 - нормальне напруження
- нормальне напруження
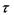 - дотичні напруження
- дотичні напруження
Напруження виміряють у Па
Отже, напруженням називається внутрішня сила віднесена до одиниці площі в даній точці
Повне напруження:
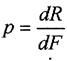 , тобто значення повного зусилля, яке припадає на одиницю площі.
, тобто значення повного зусилля, яке припадає на одиницю площі.
Очевидно: 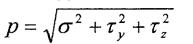
 Статичні рівняння та інтегральні рівняння рівноваги
Статичні рівняння та інтегральні рівняння рівноваги
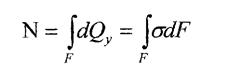
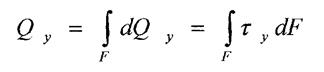
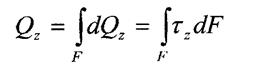
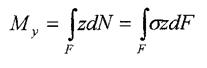
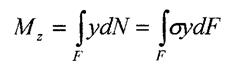
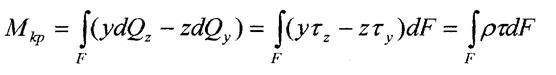
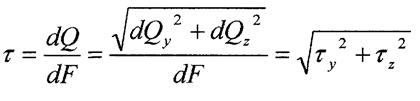
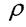 -відстань від центра ваги перерізу до лінії дій
-відстань від центра ваги перерізу до лінії дій 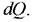
ЛЕКЦІЯ №
Геометричні характеристики плоских перерізів
Опір стержня різним видам навантаження, тобто його міцність залежить не тільки від матеріалу та розмірів стержня, а й від форми поперечного перерізу та розташування, тобто від геометричних характеристик перерізу.
Геометричні характеристики - це площа, статичний момент площі, момент інерції, радіус інерції, момент опору.
Розглянемо методи їх визначення:
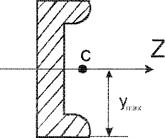
1. Статичний момент площі. Координати центра ваги.
Розглянемо довільну фігуру (поперечний переріз стержня). Добуток елемента площі 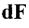 на відстань у від осі
на відстань у від осі 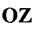 називається статичним моментом елемента площі
називається статичним моментом елемента площі 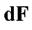 відносно осі
відносно осі 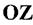 . Аналогічно для осі
. Аналогічно для осі 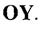
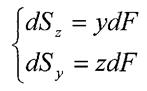
- це статичні моменти елемента 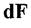 площі відносно осей
площі відносно осей  - це
- це 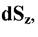 та
та  - це
- це 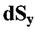
Статичний момент площі відносно осі - це сума добутків площ нескінченно малих площадок 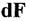 на їх відстань до цієї осі
на їх відстань до цієї осі
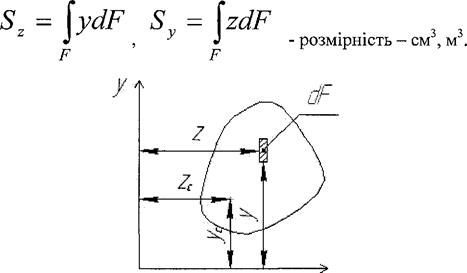
Статичний момент може бути 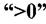 ,
, 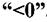 , та
, та 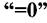 . Осі, що проходять через центр ваги і відносно яких
. Осі, що проходять через центр ваги і відносно яких 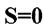 , звуться центральними
, звуться центральними
Якщо С - центр ваги перерізу, то на підставі теореми про момент рівнодійної системи сил (теорема Вариньона):
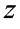
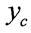
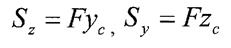
- де та с координати центра ваги, звідси
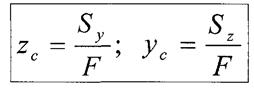 |
Для складної фігури:
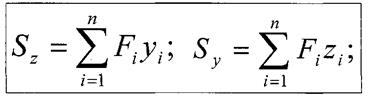
 - тут
- тут 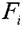 - площі елементарних фігур, на які розбивається складний переріз.
- площі елементарних фігур, на які розбивається складний переріз. 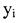 ,
, 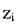 - координати центрів ваги елементів (простих фігур), беруться з урахуванням знаків.
- координати центрів ваги елементів (простих фігур), беруться з урахуванням знаків.
Координати центра ваги складного перерізу:
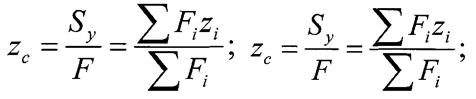
Якщо у складного перерізу є отвори, то вони додаються з від'ємною площею.
2. Моменти інерції плоских перерізів.
Осьовим моментом інерції площі фігури називають інтеграл добутків елементарних площ на квадрати їх відстаней до розглядаємої осі.
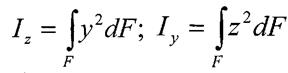
Полярний момент інерції:
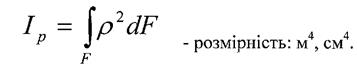
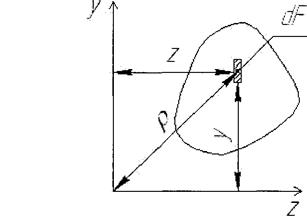
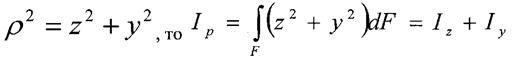 |
Якщо
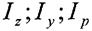 | 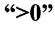 | ||
- завжди (лише додатний знак).
Відцентрований момент інерції - це інтеграл
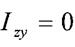
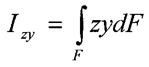
він може бути 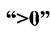 ,
, 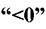 , та
, та 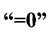 Осі відносно яких
Осі відносно яких
звуться головними осями інерції.
Дві взаємно перпендикулярні осі, з яких хоча б одна є віссю симетрії фігури, завжди будуть її головними осями інерції. Головні осі, що проходять через центр ваги перерізу, називають головними центральними осями. Осьові моменти інерції відносно головних центральних осей екстремальні, тобто один з них максимальний, інший - мінімальний.
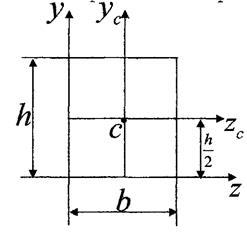
Моменти інерції відносно осей, які паралельні
центральним.
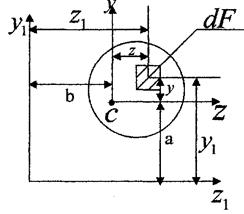 Нехай відомі моменти інерції фігури відносно центральних осей
Нехай відомі моменти інерції фігури відносно центральних осей  та
та 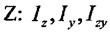
Визначим момент інерції відносно осей які паралельні центральним, тобто
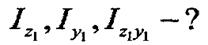
Координати довільної точки в системі 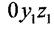 будуть дорівнювати:
будуть дорівнювати:
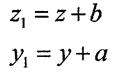 |
Підставимо 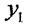 та
та 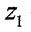 у формулу для визначення моментів інерції і проінтегруємо почлено:
у формулу для визначення моментів інерції і проінтегруємо почлено:
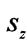
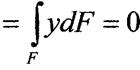
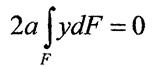
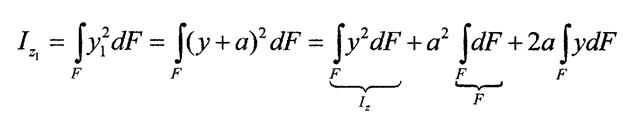
так як статичний момент площі
відносно центральної осі Z.
Тоді,
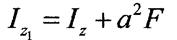 |
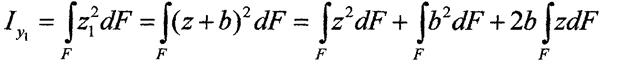 Аналогічно:
Аналогічно:
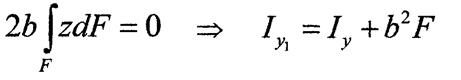
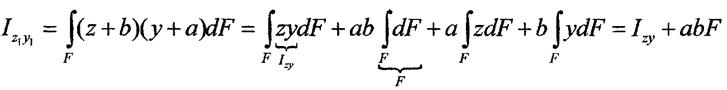
Відстані а та 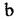 у цих формулах слід підставляти з урахуванням їх знаків.
у цих формулах слід підставляти з урахуванням їх знаків.
Визначення моментів інерції
1. Прямокутник.
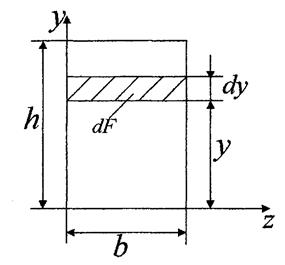
Момент інерції
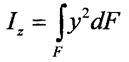 | ||
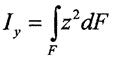 |
Площа елементарної частинки
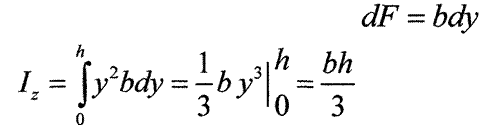 | |||
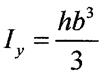 |
Аналогічно:
Момент інерції відносно центральних осей знаходимо по формулам паралельного переносу;
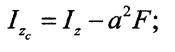
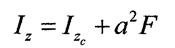
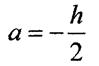 | |||||
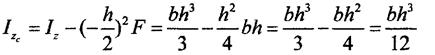 | |||||
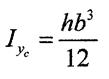 |
А налогічно:
2. Трикутники.
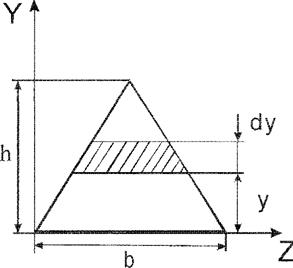 |
Момент інерції відносно осі що проходить через основу:
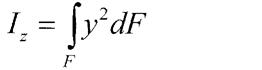 |
Площа елементарної площадки:
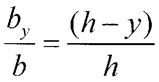
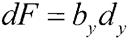
Із подібності трикутника
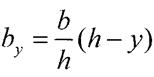
Проінтегруємо:

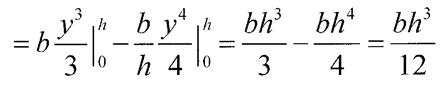
Моменти інерції відносно осей, які проходять через центр ваги трикутника знайдемо за формулами паралельного переносу
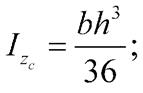 | 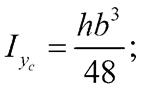 | ||
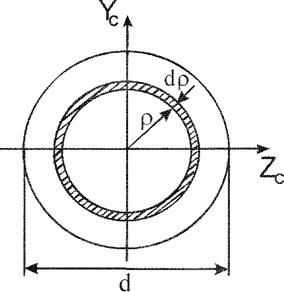
Полярний момент інерції круга:
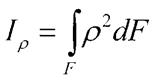
Площа елементарної площини:
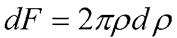
Тоді 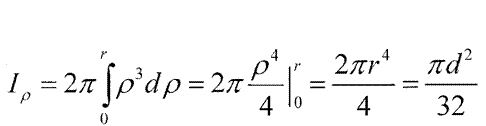
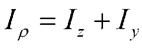 | |||
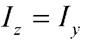 | |||
Так як а в силу симетрії
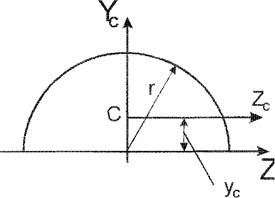
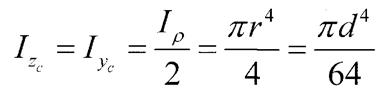
Для півкола:
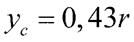
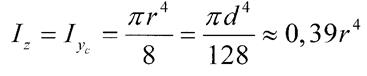

Для чверті кола
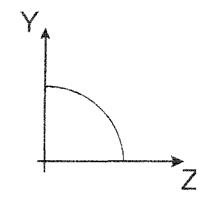
Момент інерції прокатних профілів (двотавр, кутник, швелер) визначається по таблицям сортаменту.
Момент інерції складних перерізів визначається як сума моментів інерції простих елементів на які розбивається складний переріз.
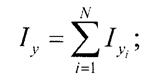
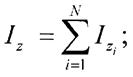
Додаються моменти інерції які беруться відносно тієї ж самої осі. Якщо в перерізі є отвори, то їх вважають елементами з від'ємною площею.
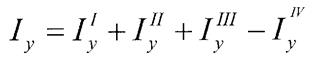
1.Радіуси інерції
Момент інерції фігури відносно будь-якої осі можна подати у вигляді добутку площі фігури на квадрат деякої величини,що називається радіусом інерції.
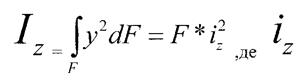
- радіус інерції відносно осі Z
Тоді радіус інерції знаходиться як
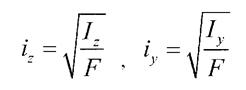 |
Моменти опору
Основний момент опору - це відношення моменту інерції відносно даної осі до відстані до найбільш віддаленої точки попереднього перерізу,тобто
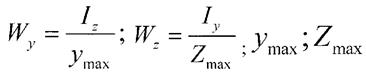
- відстані, тобто зі
знаком «+»
Практичне значення мають моменти опору,моменти інерції і радіуси інерції відносно головних центральних осей
 |
У розрахунках на міцність використовуємо момент інерції складних перерізів відносно головних центральних осей. Це такі осі,відцентрований момент відносно яких дорівнює О.Позначимо такі осі як V та U
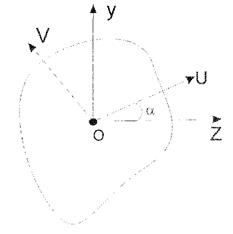 |
Повертаючи осі  та Z можна знайти таке їх положення,при якому відцентрований момент інерції дорівнюватиме О
та Z можна знайти таке їх положення,при якому відцентрований момент інерції дорівнюватиме О
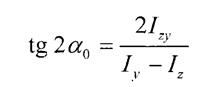 | ||||||
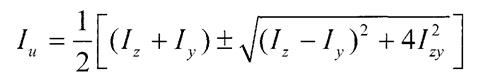 | ||||||
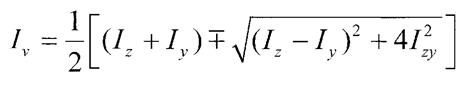 | ||||||
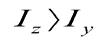 |
Верхні знаки беруть коли
ЛЕКЦІЯ №
Розтяг - стиск
Розтяг або стиск стержня спричинюється силами, що діють уздовж його осі. У цьому випадку в поперечних перерізах стержня із шести внутрішніх силових факторів виникає лише один - подовження (осьова сила 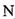 )
)
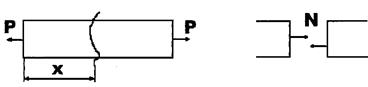 |
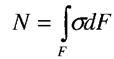
Для визначення сили  необхідно побудувати її графік, або епюру.
необхідно побудувати її графік, або епюру.
Епюра - це графік (діаграма), яка показує як змінюються внутрішні зусилля при переході від перерізу до перерізу стержня.
Правила побудови епюри:
1. Розбиваємо на ділянки.
2. Вісь (базу), на якій будується епюра, завжди вибирають так, щоб вона була паралельна або просто збігалась з віссю стержня.
3. Ординати на епюрі відкладають від осі епюри по перпендикуляру.
4. Штрихують епюри лініями, що перпендикулярні до бази.
5. Величини відкладають в певних масштабах
Поздовж сила вважається додатною, якщо вона спричинює розтяг, та від'ємною, якщо спричинює стискання.
Наприклад:
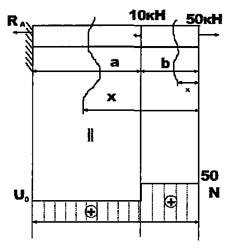 | 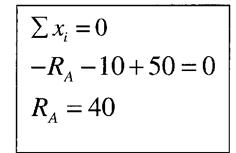 | ||
Але можна визначати реакції Ra коли будемо йти з вільного кінця.
Розсічемо стержень довільним поперечним перерізом
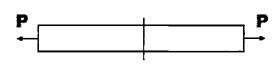 | 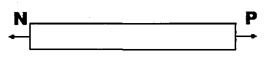 | ||
Статична сторона задачі:
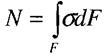 |
З цього рівняння не можна визначити напруження 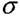 , оскільки невідомий закон розподілу їх в точках поперечного перерізу
, оскільки невідомий закон розподілу їх в точках поперечного перерізу
Геометрична сторона задачі:
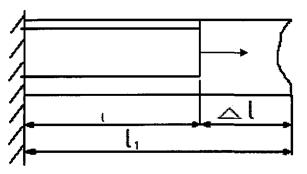 При деформації розтягу стержня поперечні перерізи стержня плоскі до деформації,
При деформації розтягу стержня поперечні перерізи стержня плоскі до деформації,
залишаються плоскими і після неї,
переміщуючись поступово вздовж осі
(гіпотеза плоских перерізів)
Таким чином всі волокна стержня
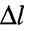 подовжуються на одну і ту саму
подовжуються на одну і ту саму
величину і їхні відносні подовження 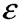 однакові
однакові
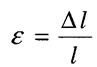 | |||
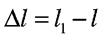 | |||
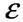 - відносне подовження або деформація (величина безрозмірна)
- відносне подовження або деформація (величина безрозмірна)
Фізична сторона задачі: полягає у встановленні залежності між деформаціями та напруженнями. При пружних деформаціях ця залежність лінійна і називається законом Гука.
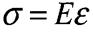
Е - модуль пружності першого роду, або модуль Юнга. Це одна з фізичних констант матеріалу, виражається в Па
Для однорідного та ізотропного матеріалу Е - стала величина тоді
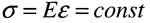 | |||
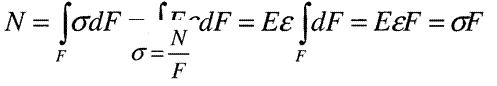 |
Якщо 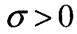 то це напруження розтягу
то це напруження розтягу
Якщо  то це напруження стиску
то це напруження стиску
Визначимо деформацію стержня
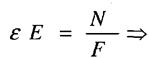
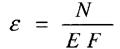 |
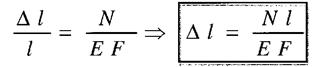
— закон Гука для
абсолютних подовжень
Добуток ЕF називається жорсткістю поперечного перерізу стержня при розтягу - стиску, а величину - називають жорсткістю стержня. Якщо на розглядуваній ділянці поздовжня сила та поперечний переріз змінні, то
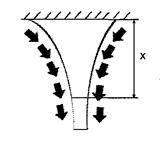 | 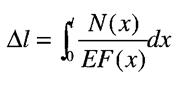 | ||
Розглянемо поперечну деформацію стержня
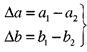
-абсолютна поперечна деформація стержня
 | |||
 | |||
При розтягу поперечні деформації від'ємні, а при стисканні додатні.
— відносна поперечна деформація. 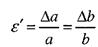
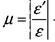 |
µ - коефіцієнт Пуассона - безрозмірна величина, яка характеризує пружні
властивості матеріалу, перебуває в межах від 0 до 0,5.
Для Корки (пробка) він 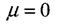
для сталі 0,3
для каучуку 0,5
Умова міцності при розтягу - стиску
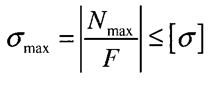
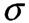 - допустиме напруження. При розтягу допустиме напруження позначають
- допустиме напруження. При розтягу допустиме напруження позначають
 при стиску
при стиску 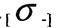

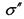 - небезпечне напруження
- небезпечне напруження
п -коефіцієнт запасу міцності
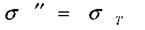 | ||||
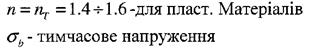 | ||||
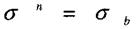 | ||||
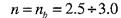 -для крихких матеріалів
-для крихких матеріалів
Види розрахунків з використання умови міцності:
1. Проектувальний розрахунок за відомими навантаженнями для вибраного матеріалу знайти з умови міцності розміри поперечного перерізу стержня.
Дані: 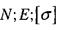 знайти:
знайти: 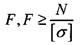
2. Перевірочний розрахунок
За відомими розмірами та матеріалом деталі перевірити, чи зможе вона витримати задане навантаження
 |
3. Визначення вантажопідйомності
За відомими розмірами деталі, матеріалом і схемою навантажування визначити допустиме навантаження
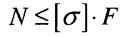 |
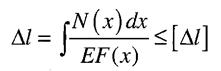 Іноді для забезпечення нормальної роботи машин та споруд розміри деталей треба вибрати так, щоб задовольнити умову жорсткості
Іноді для забезпечення нормальної роботи машин та споруд розміри деталей треба вибрати так, щоб задовольнити умову жорсткості
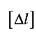
- допустиме значення зміни довжини
 |
ЛЕКЦІЯ №
ДІАГРАМА РОЗТЯГУ
При проектуванні і розрахунках на міцність треба знати властивості матеріалів. Тому матеріали випробовують на розтяг, стиск, зсув, кручення, згин та твердість. Одним із основних видів випробовувань матеріалів є випробовування на розтяг, оскільки при цьому виявляються найбільш важливі їхні властивості.
Для цього використовують спеціальні циліндричні зразки, котрі приєднують до установки та розтягують до розриву.
 |
В процесі навантаження самописцем будується діаграма розтягу: де по осі ординат відкладається зусилля, а по осі абсцис - відповідні подовження. Типовий вигляд такої діаграми:
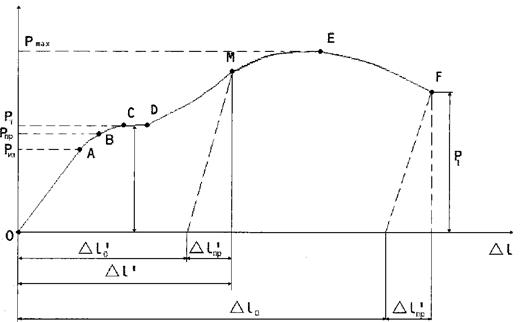 |
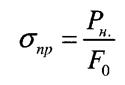 Від початку навантаження до певного значення сили має місце прямо- пропорційна залежність між подовженням зразка та силою. На діаграмі ця ділянка ОА на ній справедливий закон Гука. Позначимо силу за якої закон пропорційності припиняє свою дію через Рну. На діаграмі це точка А. Напруження, яке спричинюється силою Рну називається границею пропорційності.
Від початку навантаження до певного значення сили має місце прямо- пропорційна залежність між подовженням зразка та силою. На діаграмі ця ділянка ОА на ній справедливий закон Гука. Позначимо силу за якої закон пропорційності припиняє свою дію через Рну. На діаграмі це точка А. Напруження, яке спричинюється силою Рну називається границею пропорційності.
Тобто границею пропорційності називається напруження, після якого порушується закон Гука.
Позначимо через Рпр найбільше значення сили, при якому зразок ще не дає при розвантаженні залишкової деформації. Це точка В.
Найбільше напруження, до якого залишкова деформація при розвантаженні не виявляється, називається границею пружності.
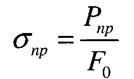 |
Границя пружності є характеристика, що не пов'язана із законом Гука. Точки
А і В знаходяться дуже близько одна від одної і як правило, різницею між  пр і
пр і 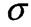 пц нехтують!!!
пц нехтують!!!
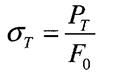 Далі іде перехід до горизонтальної площадки СД - це площадка текучості. На цій стадії подовження зразка зростає при сталому значенні розтягальної сили Рт. Такий процес деформації називається текучістю матеріалу, він супроводжується залишковим (пластичним) подовженням, яке зникає після розвантаження.
Далі іде перехід до горизонтальної площадки СД - це площадка текучості. На цій стадії подовження зразка зростає при сталому значенні розтягальної сили Рт. Такий процес деформації називається текучістю матеріалу, він супроводжується залишковим (пластичним) подовженням, яке зникає після розвантаження.
Границею текучості 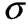 т зветься найменше напруження, при якому деформація зразка відбувається при сталому розтягальному зусиллі.
т зветься найменше напруження, при якому деформація зразка відбувається при сталому розтягальному зусиллі.
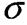 Далі (після стадії текучості) матеріал знову набирає здатності збільшувати опір деформуванню ДЕ- ділянка зміцнення. Точка Е відповідає найбілішому зусиллю Рмах яке може витримати зразок. Напруження, що відповідає максимальній силі Рмах називається тимчасовим опором, або границею міцності і позначається в
Далі (після стадії текучості) матеріал знову набирає здатності збільшувати опір деформуванню ДЕ- ділянка зміцнення. Точка Е відповідає найбілішому зусиллю Рмах яке може витримати зразок. Напруження, що відповідає максимальній силі Рмах називається тимчасовим опором, або границею міцності і позначається в
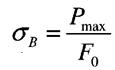
Основними характеристика пружності і міцності матеріалів є границя пружності
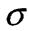 пр, границя текучості
пр, границя текучості 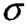 т, границя міцності(тимчасовий опір)
т, границя міцності(тимчасовий опір) 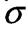 б
б
Повне подовження зразка за границею пружності складається з двох частин: пружної і пластичної.
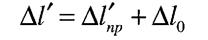 |
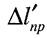
— пластична складова абсолютної деформації, не зникає.
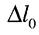 |
— пружня складова - зникає при розвантаженні
Характеристики пластичності атеріалу
1. Відносне подовження після розриву
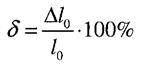
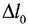 - приріст довжини після розриву
- приріст довжини після розриву
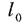 - початкова довжина
- початкова довжина
2. Відносне звуження зразка після розриву
 | |||
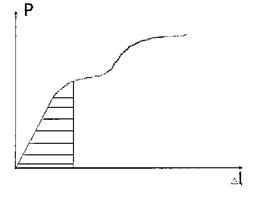 |
Робота деформації
Повна робота пружної деформації
 |
Питома робота деформації
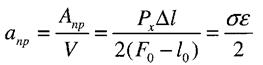 | ||||
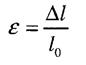 | ||||
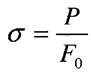 | ||||
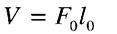 |
Питома робота деформації виражається площею трикутника на діаграмі. Діаграму в координатах 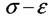 будують, щоб охарактеризувати тільки механічні характеристики матеріалу, тобто вид діаграми
будують, щоб охарактеризувати тільки механічні характеристики матеріалу, тобто вид діаграми 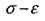 не залежить від розмірів зразка, та його площі поперечного перерізу.
не залежить від розмірів зразка, та його площі поперечного перерізу.
Лекція №
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 633; Нарушение авторских прав?; Мы поможем в написании вашей работы!