
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Неявные функции
|
|
|
|
Градиент.
Пусть 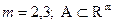 открыто,
открыто, 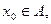
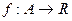 дифференцируема в точке
дифференцируема в точке  .
.
Определение 1. Вектор 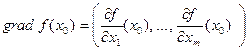 называется градиентом функции
называется градиентом функции 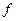 в точке
в точке  .
.
Если 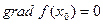 , то производная по любому направлению в точке
, то производная по любому направлению в точке  равна нулю. Допустим теперь, что
равна нулю. Допустим теперь, что 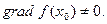 Зададимся вопросом: по какому направлению функция в данной точке
Зададимся вопросом: по какому направлению функция в данной точке  будет всего быстрее возрастать?
будет всего быстрее возрастать?
Теорема 1. Скорость роста функции 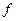 в точке
в точке  по направлению вектора
по направлению вектора 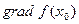 наибольшая и равна
наибольшая и равна 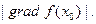
Теорема 1. Пусть:
1) функция 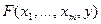 непрерывно дифференцируема в окрестности точки
непрерывно дифференцируема в окрестности точки
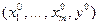 ;
;
2) 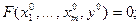
3) 
Тогда найдутся окрестности 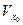 и
и 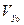 точек
точек  и
и 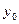 такие, что
такие, что 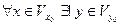 такой, что
такой, что 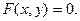 Таким образом, уравнение
Таким образом, уравнение 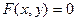
определяет на 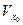 некоторую функцию
некоторую функцию 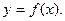 Эта функция называется неявной. Она будет дифференцируемой. Ее частные производные вычисляются по формуле
Эта функция называется неявной. Она будет дифференцируемой. Ее частные производные вычисляются по формуле
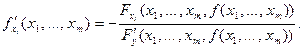
18) Классическая задача на условный экстремум.
Классической задачей на условный экстремум принято называть задачу минимизации (или максимизации) функции 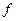 на множестве
на множестве 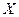 , заданном системой из конечного числа уравнений («связей»).
, заданном системой из конечного числа уравнений («связей»).
Пусть рассматривается функция  двух независимых переменных
двух независимых переменных 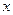 и
и 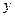 . Допустим, что множество
. Допустим, что множество 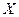 задается одним уравнением:
задается одним уравнением:
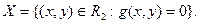
Определение 1. Точка 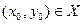 называется точкой условного локального минимума, если существует такая окрестность
называется точкой условного локального минимума, если существует такая окрестность 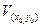 этой точки, что для всех
этой точки, что для всех 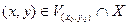
выполняется неравенство

Определение 2. Точка 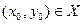 называется точкой условного локального максимума, если существует такая окрестность
называется точкой условного локального максимума, если существует такая окрестность 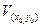 этой точки, что для всех
этой точки, что для всех 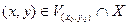
выполняется неравенство
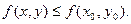
Точки локального условного минимума и локального условного максимума называются точками локального условного экстремума.
Наиболее простым способом нахождения условного экстремума функции двух переменных является сведение задачи к отысканию экстремума функции одной переменной. Этот способ применим в том случае, когда уравнение  можно разрешить относительно
можно разрешить относительно 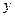 .
.
Пример 1. Найти точки локального условного экстремума функции
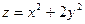 (1)
(1)
при условии
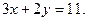 (2)
(2)
Решение. Из уравнения (2) находим, что
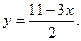 (3)
(3)
Подставляя (3) в (1), получаем
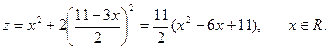 (4)
(4)
У этой функции, заданной на всей числовой оси, есть только минимум (график этой функции есть парабола, ветви которой направлены вверх). Дифференцируя (4) и приравнивая производную к нулю, получаем 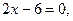 откуда
откуда 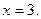 При
При 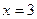 находим
находим 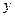 по формуле (3):
по формуле (3):  Таким образом, единственной точкой локального условного экстремума задачи (1)-(2) будет точка (3,1), являющаяся точкой локального условного минимума.
Таким образом, единственной точкой локального условного экстремума задачи (1)-(2) будет точка (3,1), являющаяся точкой локального условного минимума.
В общем случае разрешить уравнение  относительно
относительно 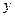 удается не всегда. Для отыскания условного локального экстремума в общем случае используется метод множителей Лагранжа. Для этого составляют функцию
удается не всегда. Для отыскания условного локального экстремума в общем случае используется метод множителей Лагранжа. Для этого составляют функцию
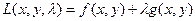
трех переменных 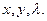 Эта функция называется функцией Лагранжа, а
Эта функция называется функцией Лагранжа, а 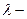 множителем Лагранжа. Справедлива следующая
множителем Лагранжа. Справедлива следующая
Теорема 1. Если точка 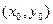 является точкой локального условного экстремума функции
является точкой локального условного экстремума функции  при условии
при условии  , то существует значение
, то существует значение 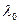 множителя Лагранжа, при котором точка
множителя Лагранжа, при котором точка 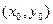 есть точка локального экстремума функции
есть точка локального экстремума функции
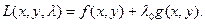
Из Теоремы 1 получаем, что 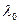 и
и 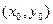 удовлетворяют системе 3х уравнений с тремя неизвестными
удовлетворяют системе 3х уравнений с тремя неизвестными
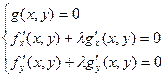 . (5)
. (5)
Из последних двух уравнений системы (5) следует, что в точке 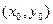 векторы
векторы 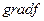 и
и  коллинеарны. Эти градиенты являются нормалями касательных к линиям уровня функций
коллинеарны. Эти градиенты являются нормалями касательных к линиям уровня функций 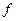 и
и 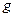 , проходящим через точку
, проходящим через точку 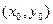 . Поэтому в точке условного экстремума линии уровня функций
. Поэтому в точке условного экстремума линии уровня функций 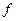 и
и 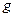 касаются.
касаются.
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 670; Нарушение авторских прав?; Мы поможем в написании вашей работы!