
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Видно, что определение дано очень строго, и это не случайно: выше мы отмечали, что строгость - отличительное свойство искусственных языков. 2 страница
|
|
|
|
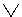 q
q  r три разных пропозициональных символа, у каждого из которых может быть одно из двух истинностных значений - либо истина, либо ложь. Рассчитаем, пользуясь правилом комбинаторики, количество сочетаний этих значений для трех символов: 23=8. Это значит, что в нашей таблице будет восемь строк. При двух пропозициональных символах было бы всего четыре строки (22=4).
Теперь приступим к построению таблицы, записывая значения символов в столбец под каждым из них:
r три разных пропозициональных символа, у каждого из которых может быть одно из двух истинностных значений - либо истина, либо ложь. Рассчитаем, пользуясь правилом комбинаторики, количество сочетаний этих значений для трех символов: 23=8. Это значит, что в нашей таблице будет восемь строк. При двух пропозициональных символах было бы всего четыре строки (22=4).
Теперь приступим к построению таблицы, записывая значения символов в столбец под каждым из них:
| р | 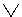
| q | 
| r |
| 0 0 0 0 1 1 1 1 | 0 0 1 1 0 0 1 1 | 0 1 0 1 0 1 0 1 |
Следует обратить внимание на алгоритм перебора сочетаний: под первым символом пишем четыре раза "0" и четыре раза "1", под вторым - попарно "0" и "1", под третьим - попеременно "0" и "1". В результате ни одна из строк не повторяет другие и учтены все комбинации истинностных значений. Осталось провести исследование логических констант, содержащихся в формуле, в соответствии с их смысловыми значениями:
| р | 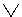
| q | 
| r |
| 0 0 0 0 1 1 1 1 | 0 0 1 1 1 1 1 1 | 0 0 1 1 0 0 1 1 | 1 1 0 1 0 1 0 1 | 0 1 0 1 0 1 0 1 |
Истинность данной формулы определяется по предпоследнему столбцу. Мы видим, что не при всех сочетаниях истинностных значений пропозициональных символов в результате получается истина. При исследовании форм высказываний встречаются три варианта. Во-первых, формула, как в нашем случае, может оказаться выполнимой, т.е. имеются сочетания значений пропозициональных символов, приводящие к истине, но имеются и не приводящие к ней. Во-вторых, формула может оказаться тождественно-истинной (общезначимой, или законом символической логики). В этом случае при любом наборе значений переменных получается истина. В-третьих, формула может оказаться тождественно-ложной, т
Лекция 6
ПОНЯТИЕ
Как было отмечено еще при рассмотрении первой темы данного лекционного курса, логика непосредственно интересуется не любым мышлением, а только абстрактным. Основными формами последнего являются понятие, суждение и умозаключение. Пришло время познакомиться с ними подробней.
| Название способа | Схема | Пример |
| Традиционный (по закону обратного отношения между содержанием и объемом) | x(A(x) 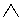 B (x)) B (x)) 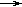 xА (х) xА (х)
| "студент-отличник" 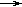 "студент" "студент"
|
| Дизъюнктивный | хА(х) 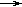 x (A (x) x (A (x) 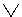 B (x)) B (x))
| "студент" 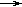 "студент или школьник" "студент или школьник"
|
| Введение существования | хА(х,a) 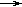 x x 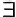 yA (x,y) yA (x,y)
| "студент, знающий астрономию" 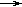 "студент, знающий какую-то науку" "студент, знающий какую-то науку"
|
| Удаление всеобщности | х 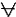 yА(х,y) yА(х,y) 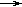 хА (х,a) хА (х,a)
| "студент, знающий любую науку" 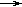 "студент, знающий астрономию" "студент, знающий астрономию"
|
От способов обобщения легко перейти к способам ограничения, если в приведенной таблице все стрелки повернуть в обратную сторону. При этом три последних способа будут называться "удаление дизъюнкции", "удаление существования" и "введение всеобщности".
| Совместимые | Несовместимые |
Равнозначные (пример: "равносторонний прямоугольник" и "равноугольный ромб") 
| Соподчиненные (пример: "грач" и "галка") 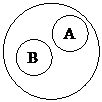
|
Перекрещивающиеся (пример: "студент" и "отличник") 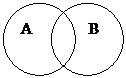
| Контрарные, или противоположные ("молчун" и "болтун") 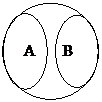
|
Субординационные (пример: "животное" и "птица") 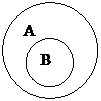
| Контрадикторные, или противоречащие друг другу (пример: "молчун" и "немолчун") 
|
|
|
|
|
|
Дата добавления: 2014-11-07; Просмотров: 227; Нарушение авторских прав?; Мы поможем в написании вашей работы!