Дисперсия света

Взаимодействие электромагнитных волн с веществом

Задачи

23.1. Плоская световая волна с длиной волны 0,6 мкм падает нормально на диафрагму с круглым отверстием диаметром 1 см. Определить расстояние от точки наблюдения до отверстия, если отверстие открывает: 1) две зоны Френеля; 2) три зоны Френеля. [1) 20,8 м; 2) 13,9 м]

23.2. Дифракционная картина наблюдается на расстоянии 1 м от точечного источника монохроматического света (l = 0,5 мкм). Посередине между источником света и экраном находится диафрагма с круглым отверстием. Определить радиус отверстия, при котором центр дифракционной картины на экране будет наиболее темным. [0,5 мм]

23.3. На щель шириной 0,2 мм падает нормально монохроматический свет с длиной волны 0,5 мкм. Экран, на котором наблюдается дифракционная картина, расположен параллельно щели на расстоянии 1 м. Определить расстояние между первыми дифракционными минимумами, расположенными по обе стороны центрального фраунгоферова максимума. [5 мм]

23.4. Определить число штрихов на 1 мм дифракционной решетки, если углу l /2 соответствует максимум пятого порядка для монохроматического света с длиной волны 0,5 мкм. [400 мм"¹]

23.5. Узкий параллельный пучок монохроматического рентгеновского излучения падает на грань кристалла с расстоянием 0,28 нм между его атомными плоскостями. Определить длину волны рентгеновского излучения, если под углом 30° к плоскости грани наблюдается дифракционный максимум второго порядка. [140 пм]

23.6. Определить постоянную дифракционной решетки, если она в первом порядке разрешает две спектральные линии калия (l₁ =578 нм и l ₂ =580 нм). Длина решетки 1 см. [34,6 мкм]

Глава 24

Дисперсией света называется зависимость показателя преломления л вещества от частоты v (длины волны l) света или зависимость фазовой скорости v световых волн (см. § 154) от его частоты v. Дисперсия света представляется в виде зависимости

(185.1)

Следствием дисперсии является разложение в спектр пучка белого света при прохождении его через призму. Первые экспериментальные наблюдения дисперсии света принадлежат И. Ньютону (1672 г.).

Рассмотрим дисперсию света в призме. Пусть монохроматический пучок света падает на призму с преломляющим углом А и показателем преломления п (рис. 268) под углом a₁. После двукратного преломления (на левой и правой гранях призмы) луч оказывается отклоненным от первоначального направления на угол j.

Рис. 268

Из рисунка следует, что

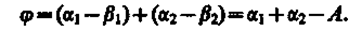(185.2)

Предположим, что углы А и a₁малы, тогда углы a₂, b₁и b₂ будут также малы и вместо синусов этих углов можно воспользоваться их значениями. Поэтому a₁/b₁ = n, b₂/a₂ = 1/n, а так как b₁ + b₂ = A, то a₂ = b₂n = n(A - b₁) = n(A - a₁/n) = nA - a₁, откуда

(185.3)

Из выражений (185.3) и (185.2) следует, что

(185.4)

т. е. угол отклонения лучей призмой тем больше, чем больше преломляющий угол призмы.

Из выражения (185.4) вытекает, что угол отклонения лучей призмой зависит от величины n - 1, а n — функция длины волны, поэтому лучи разных длин волн после прохождения призмы окажутся отклоненными на разные углы, т. е. пучок белого света за призмой разлагается в спектр, что и наблюдалось И. Ньютоном. Таким образом, с помощью призмы, так же как и с помощью дифракционной решетки, разлагая свет в спектр, можно определить его спектральный состав.

Рассмотрим различия в дифракционном и призматическом спектрах.

1. Дифракционная решетка разлагает падающий свет непосредственно по длинам волн (см. (180.3)), поэтому по измеренным углам (по направлениям соответствующих максимумов) можно вычислить длину волны. Разложение света в спектр в призме происходит по значениям показателя преломления, поэтому для определения длины волны света надо знать зависимость n = ¦(l) (185.1).

2. Составные цвета в дифракционном и призматическом спектрах располагаются различно. Из (180.3) следует, что в дифракционной решетке синус угла отклонения пропорционален длине волны. Следовательно, красные лучи, имеющие большую длину волны, чем фиолетовые, отклоняются дифракционной решеткой сильнее. Призма же разлагает лучи в спектр по значениям показателя преломления, который для всех прозрачных веществ с увеличением длины волны уменьшается (рис. 269). Поэтому красные лучи отклоняются призмой слабее, чем фиолетовые.

Величина

называемая дисперсией вещества, показывает, как быстро изменяется показатель прело мления с длиной волны. Из рис. 269 следует, что показатель преломления для прозрачных веществ с уменьшением длины волны увеличивается; следовательно, величина dn/dl по модулю также увеличивается с уменьшением l.

Рис. 269

Такая дисперсия называется нормальной. Как будет показано ниже, ход кривой n(l) — кривой дисперсии — вблизи линий и полос поглощения будет иным: n уменьшается с уменьшением l. Такой ход зависимости n от l называется аномальной дисперсией.

На явлении нормальной дисперсии основано действие призменных спектрографов. Несмотря на их некоторые недостатки (например, необходимость градуировки, различная дисперсия в разных участках спектра) при определении спектрального состава света, призменные спектрографы находят широкое применение в спектральном анализе. Это объясняется тем, что изготовление хороших призм значительно проще, чем изготовление хороших дифракционных решеток. В призменных спектрографах также легче получить большую светосилу.

Дата добавления: 2014-11-07