Функция распределения

Фазовое пространство.

Квантовая статистика.

Элементы квантовой статистики

Задачи

29.1. Определить, сколько различных волновых функций соответствует главному квантовому числу n=5.125]

29.2. Построить и объяснить диаграмму, иллюстрирующую расщепление энергетических уровней и спектральных линий (с учетом правил отбора) при переходах между состояниями с l =2 и l =1. [d®р-переход].

29.3. Принимая, что уравнению Шредингера для 1s-состояния электрона в атоме водорода удовлетворяет функция Y = Ce^-r/a (С— некоторая постоянная), показать, что a = ℏ²4pe₀/(me²),равная первому воровскому радиусу. Учесть, что 1s-состояние сферически-симметрично.

29.4. Электрон в атоме находится в f-состоянии. Определить: 1) момент импульса (орбитальный) L _l электрона; 2) максимальное значение проекции момента импульса L _lzmax на направление внешнего магнитного поля. [1) 3.46ℏ; 2) Зℏ]

29.5. Заполненной электронной оболочке соответствует главное квантовое число n = 3. Определить число электронов в этой оболочке, которые имеют одинаковые следующие квантовые числа: 1) m_s=1/2 и l = 2; 2) m_s = 1/2и m _l = 0. [1) 5; 2) 3]

29.6. Минимальная длина волны рентгеновского излучения, полученного от трубки, работающей при напряжении 50 кВ, равна 24,8 нм. Определить по этим данным постоянную Планка. [6,61×10³⁴ Дж-с]

29.7. Определить самую длинноволновую линию K-серии характеристического рентгеновского спектра, если анод рентгеновской трубки изготовлен из платины. Постоянную экранирования принять равной единице. [20 пм]

Глава 30

Квантовая статистика — раздел статистической физики, исследующий системы, которые состоят из огромного числа частиц, подчиняющихся законам квантовой механики.

В отличие от исходных положений классической статистической физики, в которой тождественные частицы различимы (частицу можно отличить от всех таких же частиц), квантовая статистика основывается на принципе неразличимости тождественных частиц (см. § 226). При этом оказывается, как будет показано ниже, что коллективы частиц с целым и полуцелым спинами подчиняются разным статистикам.

Пусть система состоит из N частиц. Введем в рассмотрение многомерное пространство всех координат и импульсов частиц системы. Тогда состояние системы определяется заданием 6N переменных, так как состояние каждой частицы определяется трой кой координат х, у, z и тройкой соответствующих проекций импульса р_х, р_у, р_z.Соответственно число «взаимно перпендикулярных» координатных осей данного про странства равно 6N. Это 6N-мерное пространство называется фазовым пространством. Каждому микросостоянию системы отвечает точка в 6N-мерном фазовом пространстве, так как задание точки фазового пространства означает задание координат и им пульсов всех частиц системы. Разобьем фазовое пространство на малые 6N-мерные элементарные ячейки объемом dqdp = dq₁dq₂ … dq_3Ndp₁dp₂...dp_3N, где q— совокупность координат всех частиц, р— совокупность проекций их импульсов. Корпускуляр-но-волновой дуализм свойств вещества (см. § 213) и соотношение неопределенностей Гейзенберга (см. § 215) приводят к выводу, что объем элементарной ячейки (он называется фазовым объемом) не может быть меньше чем h³ (h— постоянная Планка).

Вероятность dW данного состояния системы можно представить с помощью функции распределения f (q, p):

dW = f(q,p) dq dp. (234.1)

Здесь dW—вероятность того, что точка фазового пространства попадет в элемент фазового объема dqdp, расположенного вблизи данной точки q, р. Иными словами, dW представляет собой вероятность того, что система находится в состоянии, в котором ее координаты и импульсы заключены в интервале q, q+dq и р, p+dp.

Согласно формуле (234.1), функция распределения есть не что иное, как плотность вероятности определенного состояния системы. Поэтому она должна быть нормирована на единицу:

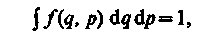
где интегрирование производится по всему фазовому пространству.

Зная функцию распределения f (q, p), можно решить основную задачу квантовой статистики — определить средние значения величин, характеризующих рассматрива емую систему. Среднее значение любой функции

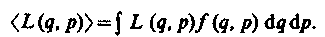(234.2)

Если иметь дело не с координатами и импульсами, а с энергией, которая квантуется, то состояние системы характеризуется не непрерывной, а дискретной функцией распределения.

Явное выражение функции распределения в самом общем виде получил американский физик Д. Гиббс (1839—1903). Оно называется каноническим распределением Гиббса. В квантовой статистике каноническое распределение Гиббса имеет вид

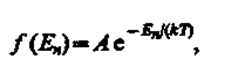(234.3)

где А — постоянная, определяемая из условия нормировки к единице, n— совокупность всех квантовых чисел, характеризующих данное состояние. Подчеркнем, что f (E_n)есть именно вероятность данного состояния, а не вероятность того, что система имеет определенное значение энергии Е_n,так как данной энергии может соответствовать не одно, а несколько различных состояний (может иметь место вырождение).

Дата добавления: 2014-11-07