КУРС ФИЗИКИ 7 страница

(38.1)

где 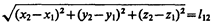— расстояние между точками трехмерного пространства, в которых эти события произошли. Введя обозначение t ₁₂ = t ₂ – t ₁, получим

Покажем, что интервал между двумя событиями одинаков во всех инерциальных системах отсчета. Обозначив D t = t ₂ – t ₁, D x = x ₂ – x ₁, D y = y ₂ – y ₁ и D z = z ₂ – z ₁, выражение (38.1) можно записать в виде

Интервал между теми же событиями в системе К' равен

(38.2)

Согласно преобразованиям Лоренца (36.3),

Подставив эти значения в (38.2), после элементарных преобразований получим, что т. е.

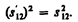
Обобщая полученные результаты, можно сделать вывод, что интервал, определяя пространственно-временные соотношения между событиями, является инвариантом при переходе от одной инерциальной системы отсчета к другой. Инвариантность интервала означает, что, несмотря на относительность длин и промежутков времени, течение событий носит объективный характер и не зависит от системы отсчета.

Теория относительности, таким образом, сформулировала новое представление о пространстве и времени. Пространственно-временные отношения являются не аб­солютными величинами, как утверждала механика Галилея — Ньютона, а относитель­ными. Следовательно, представления об абсолютном пространстве и времени являют­ся несостоятельными. Кроме того, инвариантность интервала между двумя событиями свидетельствует о том, что пространство и время органически связаны между собой и образуют единую форму существования материи — пространство-время. Простран­ство и время не существуют вне материи и независимо от нее.

Дальнейшее развитие теории относительности (общая теория относительности, или теория тяготения) показало, что свойства пространства-времени в данной области определяются действующими в ней полями тяготения. При переходе к космическим масштабам геометрия пространства-времени не является евклидовой (т. е. не завися­щей от размеров области пространства-времени), а изменяется от одной области к другой в зависимости от концентрации масс в этих областях и их движения.

§ 39. Основной закон релятивистской динамики материальной точки

Масса движущихся релятивистских частиц зависит от их скорости:

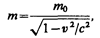(39.1)

где m ₀ — масса покоя частицы, т. е. масса, измеренная в той инерциальной системе отсчета, относительно которой частица находится в покое; с — скорость света в ваку­уме; т — масса частицы в системе отсчета, относительно которой она движется со скоростью v. Следовательно, масса одной и той же частицы различна в разных инерциальных системах отсчета.

Из принципа относительности Эйнштейна (см. § 35), утверждающего инвариант­ность всех законов природы при переходе от одной инерциальной системы отсчета к другой, следует условие инвариантности уравнений физических законов относительно преобразований Лоренца. Основной закон динамики Ньютона

оказывается также инвариантным по отношению к преобразованиям Лоренца, если в нем справа стоит производная по времени от релятивистского импульса.

Основной закон релятивистской динамики материальной точки имеет вид

(39.2)

или

(39.3)

где

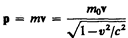(39.4)

— релятивистский импульс материальной точки.

Отметим, что уравнение (39.3) внешне совпадает с основным уравнением ньюто­новской механики (6.7). Однако физический смысл его другой: справа стоит производ­ная по времени от релятивистского импульса, определяемого формулой (39.4). Таким образом, уравнение (39.2) инвариантно по отношению к преобразованиям Лоренца и, следовательно, удовлетворяет принципу относительности Эйнштейна. Следует учиты­вать, что ни импульс, ни сила не являются инвариантными величинами. Более того, в общем случае ускорение не совпадает по направлению с силой.

В силу однородности пространства (см. § 9) в релятивистской механике выполняет­ся закон сохранения релятивистского импульса: релятивистский импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени. Часто вообще не оговаривают, что рассматривают релятивистский импульс, так как если тела движутся со скоростями, близкими к с, то можно использовать только релятивистское выраже­ние для импульса.

Анализ формул (39.1), (39.4) и (39.2) показывает, что при скоростях, значительно меньших скорости с, уравнение (39.2) переходит в основной закон (см. (6.5)) классичес­кой механики. Следовательно, условием применимости законов классической (ньюто­новской) механики является условие v<<c. Законы классической механики получаются как следствие теории относительности для предельного случая v<<c (формально пере­ход осуществляется при с ®¥). Таким образом, классическая механика — это меха­ника макротел, движущихся с малыми скоростями (по сравнению со скоростью света в вакууме).

Экспериментальное доказательство зависимости массы от скорости (39.1) является подтверждением справедливости специальной теории относительности. В дальнейшем (см. § 116) будет показано, что на основании этой зависимости производятся расчеты ускорителей.

§ 40. Закон взаимосвязи массы и энергии

Найдем кинетическую энергию релятивистской частицы. Раньше (§ 12) было показано, что приращение кинетической энергии материальной точки на элементарном переме­щении равно работе силы на этом перемещении:

(40.1)

Учитывая, что dr = v d t, и подставив в (40.1) выражение (39.2), получаем

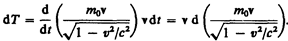
Преобразовав данное выражение с учетом того, что vdv = v d v, и формулы (39.1), придем к выражению

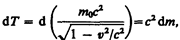(40.2)

т. е. приращение кинетической энергии частицы пропорционально приращению ее массы.

Так как кинетическая энергия покоящейся частицы равна нулю, а ее масса равна массе покоя m ₀, то, проинтегрировав (40.2), получим

(40.3)

или кинетическая энергия релятивистской частицы имеет вид

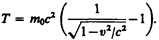(40.4)

Выражение (40.4) при скоростях v«c переходит в классическое:

(разлагая в ряд при v << c, правомерно пренебречь чле­нами второго порядка малости).

А. Эйнштейн обобщил положение (40.2), предположив, что оно справедливо не только для кинетической энергии частицы, но и для полной энергии, а именно любое изменение массы D m сопровождается изменением полной энергии частицы,

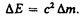(40.5)

Отсюда А. Эйнштейн пришел к универсальной зависимости между полной энергией тела Е и его массой т:

(40.6)

Уравнение (40.6), равно как и (40.5), выражает фундаментальный закон природы — за­кон взаимосвязи (пропорциональности) массы и энергии: полная энергия системы равна произведению ее массы на квадрат скорости света в вакууме. Отметим, что в полную энергию Е не входит потенциальная энергия тела во внешнем силовом поле.

Закон (40.6) можно, учитывая выражение (40.3), записать в виде

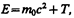
откуда следует, что покоящееся тело (T =0) также обладает энергией

называемой энергией покоя. В классической механике энергия покоя Е ₀ не учитывается, считая, что при v =0 энергия покоящегося тела равна нулю.

В силу однородности времени (см. § 13) в релятивистской механике, как и в клас­сической, выполняется закон сохранения энергии: полная энергия замкнутой системы сохраняется, т. е. не изменяется с течением времени.

Из формул (40.6) и (39.4) найдем релятивистское соотношение между полной энергией и импульсом частицы:

(40.7)

Возвращаясь к уравнению (40.6), отметим еще раз, что оно имеет универсальный характер. Оно применимо ко воем формам энергии, т. е. можно утверждать, что с энергией, какой бы формы она ни была, связана масса

(40.8)

и, наоборот, со всякой массой связана энергия (40.6).

Чтобы охарактеризовать прочность связи и устойчивость системы каких-либо частиц (например, атомного ядра как системы из протонов и нейтронов), вводят понятие энергии связи. Энергия связи системы равна работе, которую необходимо затратить, чтобы разложить эту систему на составные части (например, атомное ядро — на протоны и нейтроны). Энергия связи системы

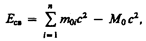(40.9)

где m _{0 i} — масса покоя i -й частицы в свободном состоянии; М ₀ — масса покоя системы, состоящей из п частиц.

Закон взаимосвязи (пропорциональности) массы и энергии блестяще подтвержден экспериментом о выделении энергии при протекании ядерных реакций. Он широко используется для расчета энергетических эффектов при ядерных реакциях и превраще­ниях элементарных частиц.

Рассматривая выводы специальной теории относительности, видим, что она, как, впрочем, и любые крупные открытия, потребовала пересмотра многих установившихся и ставших привычными представлений. Масса тела не остается постоянной величиной, а зависит от скорости тела; длина тел и длительность событий не являются абсолют­ными величинами, а носят относительный характер; наконец, масса и энергия оказа­лись связанными друг с другом, хотя они и являются качественно различными свойст­вами материи.

Основной вывод теории относительности сводится к тому, что пространство и вре­мя органически взаимосвязаны и образуют единую форму существования мате­рии — пространство-время. Только поэтому пространственно-временной интервал между двумя событиями является абсолютным, в то время как пространственные и временны2е промежутки между этими событиями относительны. Следовательно, вытекающие из преобразований Лоренца следствия являются выражением объективно существующих пространственно-временны2х соотношений движущейся материи.

7.1. Определить собственную длину стержня (длину, измеренную в системе, относительно которой стержень покоится), если в лабораторной системе (системе отсчета, связанной с измерительными приборами) его скорость v = 0,8 с, длина l = 1 м и угол между ним и направлением движения q = 30°.

7.2. Собственное время жизни частицы отличается на 1,5% от времени жизни по неподвижным часам. Определить b = v / с. [0,172]

7.3. Тело, масса покоя которого 2 кг, движется со скоростью 200 Мм/с в системе K', перемеща­ющейся относительно системы К со скоростью 200 Мм/с. Определить: 1) скорость тела относи­тельно системы К; 2) его массу в этой системе. [1) 277 Мм/с; 2) 5,2 кг]

7.4. Воспользовавшись тем, что интервал — инвариантная величина по отношению к преобразо­ваниям координат, определить расстояние, которое пролетел p-мезон с момента рождения до распада, если время его жизни в этой системе отсчета D t = 5 мкс, а собственное время жизни (время, отсчитанное по часам, движущимся вместе с телом) D t ₀ =2,2 мкс. [1,35 км]

7.5. Определить скорость, при которой релятивистский импульс частицы превышает ее ньютонов­ский импульс в пять раз. [0,98 с]

7.6. Определить скорость, полученную электроном, если он прошел ускоряющую разность по­тенциалов 1,2 МэВ. [2,86 Мм/с]

7.7. Определить релятивистский импульс электрона, кинетическая энергия которого 1 ГэВ. [5,34×10^–19 Н×с]

2 ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ

Глава 8 Молекулярно-кинетическая теория идеальных газов

§ 41. Статистический и термодинамический методы. Опытные законы идеального газа

Статистический и термодинамический методы исследования. Молекулярная физика и термодинамика — разделы физики, в которых изучаются макроскопические процессы в телах, связанные с огромным числом содержащихся в телах атомов и молекул. Для исследования этих процессов применяют два качественно различных и взаимно допол­няющих друг друга метода: статистический (молекулярно-кинетический) и термодинами­ческий. Первый лежит в основе молекулярной физики, второй — термодинамики.

Молекулярная физика — раздел физики, изучающий строение и свойства вещества исходя из молекулярно-кинетических представлений, основывающихся на том, что все тела состоят из молекул, находящихся в непрерывном хаотическом движении.

Идея об атомном строении вещества высказана древнегреческим философом Демо­критом (460—370 до н. э.). Атомистика возрождается вновь лишь в XVII в. и развива­ется в работах М. В. Ломоносова, взгляды которого на строение вещества и тепловые явления были близки к современным. Строгое развитие молекулярной теории относит­ся к середине XIX в. и связано с работами немецкого физика Р. Клаузиуса (1822—1888), Дж. Максвелла и Л. Больцмана.

Процессы, изучаемые молекулярной физикой, являются результатом совокупного действия огромного числа молекул. Законы поведения огромного числа молекул, являясь статистическими закономерностями, изучаются с помощью статистического метода. Этот метод основан на том, что свойства макроскопической системы в конеч­ном счете определяются свойствами частиц системы, особенностями их движения и усредненными значениями динамических характеристик этих частиц (скорости, энер­гии и т. д.). Например, температура тела определяется скоростью хаотического движе­ния его молекул, но так как в любой момент времени разные молекулы имеют различные скорости, то она может быть выражена только через среднее значение скорости движения молекул. Нельзя говорить о температуре одной молекулы. Таким образом, макроскопические характеристики тел имеют физический смысл лишь в слу­чае большого числа молекул.

Термодинамика — раздел физики, изучающий общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, и процессы перехо­да между этими состояниями. Термодинамика не рассматривает микропроцессы, кото­рые лежат в основе этих превращений. Этим термодинамический метод отличается от статистического. Термодинамика базируется на двух началах — фундаментальных за­конах, установленных в результате обобщения опытных данных.

Область применения термодинамики значительно шире, чем молекулярно-кинетической теории, ибо нет таких областей физики и химии, в которых нельзя было бы пользоваться термодинамическим методом. Однако, с другой стороны, термодинами­ческий метод несколько ограничен: термодинамика ничего не говорит о микроскопи­ческом строении вещества, о механизме явлений, а лишь устанавливает связи между макроскопическими свойствами вещества. Молекулярно-кинетическая теория и термо­динамика взаимно дополняют друг друга, образуя единое целое, но отличаясь различ­ными методами исследования.

Термодинамика имеет дело с термодинамической системой — совокупностью мак­роскопических тел, которые взаимодействуют и обмениваются энергией как между собой, так и с другими телами (внешней средой). Основа термодинамического мето­да — определение состояния термодинамической системы. Состояние системы задает­ся термодинамическими параметрами (параметрами состояния) — совокупностью физи­ческих величин, характеризующих свойства термодинамической системы. Обычно в ка­честве параметров состояния выбирают температуру, давление и удельный объем.

Температура — одно из основных понятий, играющих важную роль не только в термодинамике, но и в физике в целом. Температура — физическая величина, харак­теризующая состояние термодинамического равновесия макроскопической системы. В соответствии с решением XI Генеральной конференции по мерам и весам (1960) в настоящее время можно применять только две температурные шкалы — термодина­мическую и Международную практическую, градуированные соответственно в кельвинах (К) и в градусах Цельсия (°С). В Международной практической шкале тем­пература замерзания и кипения воды при давлении 1,013×10⁵ Па соответственно 0 и 100°С (реперные точки).

Термодинамическая температурная шкала определяется по одной реперной точке, в качестве которой взята тройная точка воды (температура, при которой лед, вода и насыщенный пар при давления 609 Па находятся в термодинамическом равновесии). Температура этой точки по термодинамической шкале равна 273,16 К (точно). Градус Цельсия равен кельвину. В термодинамической шкале температура замерзания воды равна 273,15 К (при том же давлении, что и в Международной практической шкале), поэтому, по определению, термодинамическая температура и температура по Между­народной практической шкале связаны соотношением

Т = 273,15 + t.

Температура T = 0 К называется нулем кельвин. Анализ различных процессов показывает, что 0 К недостижим, хотя приближение к нему сколь угодно близко возможно.

Удельный объем v — это объем единицы массы. Когда тело однородно, т. е. его плотность r = const, то v=V/m= 1 /p. Так как при постоянной массе удельный объем пропорционален общему объему, то макроскопические свойства однородного тела можно характеризовать объемом тела.

Параметры состояния системы могут изменяться. Любое изменение в термодина­мической системе, связанное с изменением хотя бы одного из ее термодинамических параметров, называется термодинамическим процессом. Макроскопическая система на­ходится в термодинамическом равновесии, если ее состояние с течением времени не меняется (предполагается, что внешние условия рассматриваемой системы при этом не изменяются).

В молекулярно-кинетической теории пользуются идеализированной моделью идеаль­ного газа, согласно которой считают, что:

1) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда;

2) между молекулами газа отсутствуют силы взаимодействия;

3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.

Модель идеального газа можно использовать при изучении реальных газов, так как они в условиях, близких к нормальным (например, кислород и гелий), а также при низких давления» и высоких температурах близки по своим свойствам к идеальному газу. Кроме того, внеся поправки, учитывающие собственный объем молекул газа и действующие молекулярные силы, можно перейти к теории реальных газов.

Рассмотрим законы, описывающие поведение идеальных газов.

Закон Бойля—Мариотта *: для данной массы газа при постоянной температуре произведение давления газа на его объем есть величина постоянная:

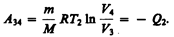(41.1)

* Р. Бойль (1627—1691)—английский ученый; Э. Мариотт (1620—1684) — французский физик.

Кривая, изображающая зависимость между величинами р и V, характеризующими свойства вещества при постоянной температуре, называется изотермой. Изотермы представляют собой гиперболы, расположенные на графикетем выше, чем выше температура, при которой происходит процесс (рис. 60).

Законы Гей-Люссака *:1) объем данной массы газа при постоянном давлении изменяется линейно с температурой:

(41.2)

2) давление данной массы газа при постоянном объеме изменяется линейно с тем­пературой:

(41.3)

* Ж. Гей-Люссак (1778—1850) — французский ученый.

В этих уравнениях t — температура по шкале Цельсия, р ₀ и V ₀ — давление и объем при 0°С, коэффициент a = 1/273,15 К^–1.

Процесс, протекающий при постоянном давлении, называется изобарным. На диа­грамме в координатах V, t (рис. 61) этот процесс изображается прямой, называемой изобарой. Процесс, протекающий при постоянном объеме, называется изохорным. На диаграмме в координатах р, t (рис. 62) он изображается прямой, называемой изохорой.

Из (41.2) и (41.3) следует, что изобары и изохоры пересекают ось температур в точке t=– 1 /a=– 273,15°С, определяемой из условия 1+a t = 0. Если перенести начало отсчета в эту точку, то происходит переход к шкале Кельвина (рис. 62), откуда

Вводя в формулы (41.2) и (41.3) термодинамическую температуру, законам Гей-Люссака можно придать более удобный вид:

(41.4)

(41.5)

где индексы 1 и 2 относятся к произвольным состояниям, лежащим на одной изобаре или изохоре.

Закон Авогадро *: моли любых газов при одинаковых температуре и давлении занимают одинаковые объемы. При нормальных условиях этот объем равен 22,41×10^–3 м³/моль.

* А. Авогадро (1776—1856) — итальянский физики химик.

По определению, в одном моле различных веществ содержится одно и то же число молекул, называемое постоянной Авогадро:

Закон Дальтона *: давление смеси идеальных газов равно сумме парциальных давлений p ₁, p ₂ ,..., р_n входящих в нее газов:

Парциальное давление — давление, которое производил бы газ, входящий в состав газовой смеси, если бы он один занимал объем, равный объему смеси при той же температуре.

* Дж. Дальтон (1766—1844) — английский химик и физик.

§ 42. Уравнение Клапейрона — Менделеева

Как уже указывалось, состояние некоторой массы газа определяется тремя термодина­мическими параметрами: давлением р, объемом V и температурой Т. Между этими параметрами существует определенная связь, называемая уравнением состояния, кото­рое в общем виде дается выражением

где каждая из переменных является функцией двух других.

Французский физик и инженер Б. Клапейрон (1799—1864) вывел уравнение состоя­ния идеального газа, объединив законы Бойля — Мариотта и Гей-Люссака. Пусть некоторая масса газа занимает объем V ₁, имеет давление р ₁ и находится при тем­пературе T ₁. Эта же масса газа в другом произвольном состоянии характеризуется параметрами р ₂, V ₂, T ₂ (рис. 63). Переход из состояния 1 в состояние 2 осуществляется в виде двух процессов: 1) изотермического (изотерма 1–1'), 2) изохорного (изохора 1'–2).

В соответствии с законами Бойля — Мариотта (41.1) и Гей-Люссака (41.5) за­пишем:

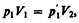(42.1)

(42.2)

Исключив из уравнений (42.1) и (42.2) получим

Так как состояния 1 и 2 были выбраны произвольно, то для данной массы газа величина pV/T остается постоянной, т. е.

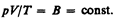(42.3)

Выражение (42.3) является уравнением Клапейрона, в котором В — газовая постоянная, различная для разных газов.

Русский ученый Д. И. Менделеев (1834—1907) объединил уравнение Клапейрона с законом Авогадро, отнеся уравнение (42.3) к одному молю, использовав молярный объем V _m. Согласно закону Авогадро, при одинаковых р и Т моли всех газов занимают одинаковый молярный объем V _m, поэтому постоянная В будет одинаковой для всех газов. Эта общая для всех газов постоянная обозначается R и называется молярном газовой постоянной. Уравнению

(42.4)

удовлетворяет лишь идеальный газ, и оно является уравнением состояния идеального газа, называемым также уравнением Клапейрона — Менделеева.

Числовое значение молярной газовой постоянной определим из формулы (42.4), полагая, что моль газа находится при нормальных условиях (р ₀ = 1,013×10⁵ Па, T ₀=273,15 К, V _m=22,41×10^–3 м³/моль): R =8,31 Дж/(моль×К).

От уравнения (42.4) для моля газа можно перейти к уравнению Клапейро­на — Менделеева для произвольной массы газа. Если при некоторых заданных давле­нии и температуре один моль газа занимает молярный объем V _m, то при тех же условиях масса т газа займет объем V= (т/М)V _m, где М — молярная масса (масса одного моля вещества). Единица молярной массы — килограмм на моль (кг/моль). Уравнение Клапейрона — Менделеева для массы т газа

(42.5)

где n =m/M — количество вещества.

Часто пользуются несколько иной формой уравнения состояния идеального газа, вводя постоянную Больцмана:

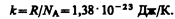
Исходя из этого уравнение состояния (42.4) запишем в виде

где N _A /V _m = n — концентрация молекул (число молекул в единице объема). Таким образом, из уравнения

(42.6)

следует, что давление идеального газа при данной температуре прямо пропорциональ­но концентрации его молекул (или плотности газа). При одинаковых температуре и давлении все газы содержат в единице объема одинаковое число молекул. Число молекул, содержащихся в 1 м³ газа при нормальных условиях, называется числом Лошмидта *:

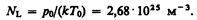
* И. Лошмидт (1821—1895) —австрийский химик и физик.

Дата добавления: 2014-11-07