Определение ускорения свободного падения с помощью математического маятника для города Белгорода

ЛАБОРАТОРНАЯ РАБОТА № 1.

Средств измерения

Абсолютные инструментальные погрешности

Средства измерения	Предел измерения	Цена деления	Абсолютная инструментальная погрешность
Линейка ученическая чертёжная	До 50 см	1 мм	±1 мм
Весы учебные	200 г	-	±0,01 г
Секундомер	0-30 мин	0,2	±1 с за 30 мин
Штангенциркуль	150 мм	0,1мм	±0,05 мм
Микрометр	25 мм	0,01мм	±0,005 мм
Термометр лабораторный	0-100^0 С	1 ^0С	±1 ^0С
Амперметр школьный	2 А	0,1 А	±0,05 А
Вольтметр школьный	6 В	0,2 В	±0,15 В

Для определения абсолютной инструментальной погрешности прибора надо знать его класс точности. Класс точности g прибора показывает, сколько процентов составляет абсолютная инструментальная погрешность от всей шкалы прибора.

Класс точности указывается на шкале прибора или в его паспорте (знак % при этом не пишется). Существуют следующие классы точности электроизмерительных приборов: 1; 0,2; 0,5; 1; 1,5; 2,5; 4. Зная класс точности прибора (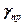) и всю шкалу (A_max), определяют абсолютную погрешность измерения физической величины этим прибором: .

Цель работы: определить ускорение свободного падения с помощью математического маятника для города Белгорода.

Теория. Математическим маятником называется точка, подвешенная на невесомой и нерастяжимой нити. Моделью может служить тяжелый шарик, размеры которого весьма малы по сравнению с длиной нити, на которой он подвешен (т.е. несравнимы с расстоянием от центра тяжести до точки подвеса).

Ученые Галилей, Ньютон, Бессель и другие установили следующие законы математического маятника.

1. Период колебания математического маятника не зависит от массы маятника и от амплитуды, если угол размаха не превышает 6°.

2. Период колебания математического маятника прямо пропорционален квадратному корню из длины маятника и обратно пропорционален квадратному корню из ускорения свободного падения. На основании этих законов можно записать формулу для периода колебания Т:

,

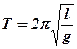Этой формулой можно воспользоваться для определения ускорения свободного падения для конкретной местности:

,

Приборы и принадлежности: штатив с держателем, шарик, подвешенный на почти нерастяжимой нити длиной около 1м, измерительная лента, секундомер.

Порядок выполнения работы:

1. Чтобы определить ускорение свободного падения, необходимо определить период колебания математического маятника. Для этого нужно:

1.1. Поставить штатив на край стола так, чтобы к нему можно было подвесить маятник длиной более 1 м.

2. Определить длину нити маятника l. Для этого нужно измерить длину нити и радиус шарика и полученные величины сложить, т.е. l = l _нити + r_шара.

2.1. Вывести маятник из положения равновесия на 5 – 7 см (амплитуда колебаний должна быть не большой).

2.2. Отсчитать 100 полных колебаний и одновременно с помощью секундомера засечь время этих колебаний.

2.3. При выполнении работы следует следить за тем, чтобы точка подвеса была неподвижной.

2.4. Вычислить время одного полного колебания по формуле: , где t - время полных 100 колебаний.

3. Повторить опыт всего 3 раза, каждый раз изменяя длину нити на 3-5 см, используя пункт работы 1 – 2.4.

4. Вычислить ускорения свободного падения с помощью формулы:

4.1. Найти среднее значение ускорения свободного падения по формуле:

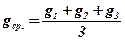
1. Определить относительную погрешность метода по формуле:

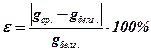, где g_белг. = 9,83 м/с² – ускорение свободного падения в г. Белгороде.

2. Результат измерений и вычислений занести в таблицу 6.1.

Таблица 6.1.

№ п/п	l, м	t, c	Т, с	g, м/с^2	gср., м/с^2	, %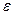

7. Сделать вывод, ответить на контрольные вопросы.

8. Ответить на контрольные вопросы.

Контрольные вопросы:

1. Что называется математическим маятником?

2. Зависит ли ускорение свободного падения от широты местности, высоты над поверхностью земли? Если зависит, то почему?

3. Можно ли пользоваться маятниковыми часами в условиях невесомости?

4. В каких положениях действующая на шарик возвращающая сила будет максимальна, равна нулю?

5. Наблюдая за движением шарика в течение одного периода, ответьте на вопрос: будет ли оно равноускоренным?

6. Изменится ли результат определения ускорения свободного падения, если проделать опыт с шариком другой массы? С нитью другой длины?

Дата добавления: 2014-11-07