Лабораторная работа №4. Разработка алгоритмов итерационной структуры

Тема: Разработка алгоритмов итерационной циклической структуры (10 ч.)

Цель работы: овладеть практическими навыками разработки алгоритмов и программ итерационной циклической структуры.

Изучить:

- организацию итерационных процессов;

- приемы алгоритмизации: уточнение корня уравнения методом итераций, вычисление суммы членов бесконечного ряда, накопление суммы.

- разработать алгоритмы и программы решения задач

Задание

1. Методом итераций вычислить корень уравнения вида f(x)=0, расположенный на отрезке [a, b] с заданной абсолютной погрешностью. Определить также число итераций, необходимое для нахождения корня. Задание выполнить в соответствии с вариантом.

№	Уравнение	Отрезок	точность

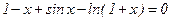
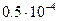
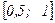
Метод простой итерации решения уравнения f(x)=0 заключается в следующем:

1. исходное уравнение приводится к виду x =g(x);

2. за начальное решение x0 принимается любое значение x из отрезка [a, b];

3. строится итерационный процесс

где i = 1, 2, 3, …,

который завершается при условии , где e- заданная точность решения уравнения.

Примечание: примеры подобраны так, чтобы итерационный процесс сходился, (сходимость метода зависит и от вида функции g(x), в случае, если процесс будет расходиться, то поменяйте вид функции g(x)).

Пример выполнения задания: Методом простой итерации найти решение уравнения x³-2x-3=0 принадлежащее отрезку [2, 3] с заданной абсолютной погрешностью e. Приведем уравнение к виду .

Исходные данные: a, b и Eps; Результат: x1; Промежуточные данные: x0;

Комментарии к строкам программы.

8.- 13. строки диалоговый ввод значений исходных данных с клавиатуры;

15. – начало цикла “До ” (Repeat);

16.- 17. вычисление очередного значения корня уравнения (тело цикла);

18.– оператор заканчивает цикл, если условие выполняется и продолжает его в противном случае;

19. – 20. Вывод решения уравнения;

21.- Ожидания нажатия клавиши Enter.

2. Написать алгоритм вычисления суммы членов бесконечного ряда с заданной точностью. На печать вывести значение суммы и число членов ряда, вошедших в сумму. Задание выполнить в соответствии с вариантом.

№	Сумма членов ряда	Значение x	Точность
		0,20
		0,10
		0,15
		0,12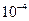
		0,70
		---
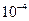
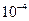
		1,5
		1,7
		0,75
		0,62
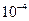
		0,20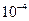
		0,30
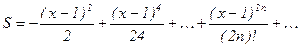
		0,25
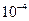
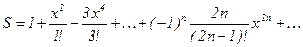
		0,75

Пример выполнения задания. Написать алгоритм и программу вычисления при заданном значении x суммы членов бесконечного ряда с точностью e. На печать вывести значение суммы и число членов ряда, вошедших в сумму.

, где n!=1×2× 3× ¼× n.

Воспользуемся соотношением между предыдущим и последующим слагаемыми: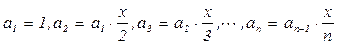

Исходные данные: x и Eps; Результат: S; Промежуточные данные: a и n;

3. Написать алгоритм вычисления определенного интеграла на заданном отрезке двумя различными методами (методом прямоугольников и трапеций). Считать заданным число разбиений отрезка интегрирования и численный метод. Задание выполнить в соответствии с вариантом.

№	Интегрируемая функция	Число отрезков	Интервал [a, b]	Точность
			[1; 4]
			[1; 2,5]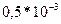
			[1; 3]
			[0; p/2]
			[0; p/2]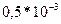
			[0; 1]
			[1; 2,5]
			[0; 3]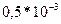
			[0; 2]
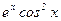
			[0; p]
			[1; 2]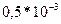
			[1; 2]
			[0; 2]
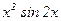
			[1; 2]
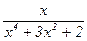
			[1; 2]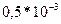
			[0; p]

Пример выполнения задания: Вычислить приближенное значение определенного интеграла с заданной точностью e, используя следующие формулы для вычисления:

-формула прямоугольников

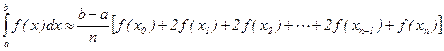-формула трапеций.

Для вычисления интеграла воспользуемся методом прямоугольников, приведем алгоритм и программу решения задачи при фиксированном n (а), а затем с заданной точностью (с помощью вложенных циклов) (б).

а) алгоритм и программа решения задачи при фиксированном n (метод прямоугольников);

Исходные данные: a, b и n; Результат: S; Промежуточные данные: h, x;

Некоторые комментарии к программе:

Строки 16 –19 образуют цикл “Пока…”. Пока x<=b выполняется тело цикла (строки 17 и 18).

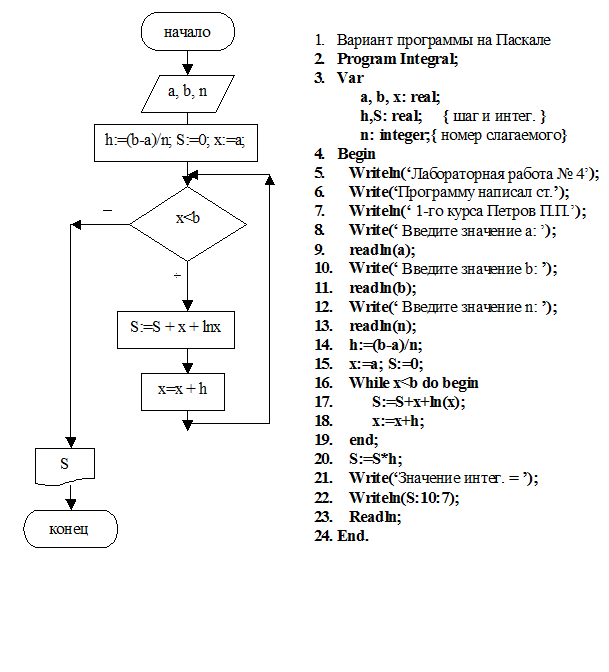
б) алгоритм и программа решения задачи с заданной точностью (метод прямоугольников).

Исходные данные: a, b и Eps; Результат: S2;

Промежуточные данные: h, x, n, S1;

Некоторые комментарии к программе:

Строки 15–25 образуют структуру вложенных циклов: внешний цикл “До…” (Repeat) и внутренний цикл “Пока…” (While) строки 19-22.

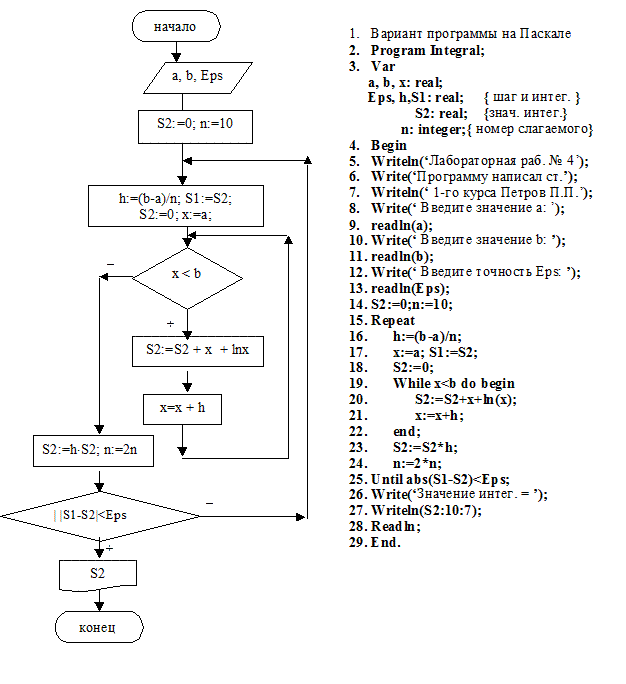
Пример алгоритма и программы вычисления интеграла методом трапеций с заданной точностью.

Исходные данные: a, b и Eps; Результат: S2;

Промежуточные данные: h, x, n, S1;

Некоторые комментарии к программе:

Строки 14–24 образуют структуру вложенных циклов: внешний цикл “До…” (Repeat) и внутренний цикл “Пока…” (While) строки 18-21.

Внешний цикл используется для уточнения значения суммы. Перед повторным выполнением этого цикла значение n (количество точек разбиения отрезка) увеличивается в два раза.

Внутренний цикл используется для вычисления текущего значения суммы (S2).

Дата добавления: 2014-11-07