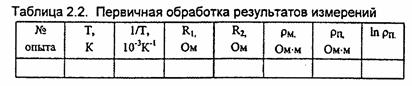
Обработка результатов. 1. В табл. 2.2 запишите результаты вычислений температуры Т

1. В табл. 2.2 запишите результаты вычислений температуры Т. сопротивления и удельного сопротивления 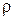образцов, а также 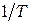и 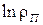. Приведите примеры вычислений всех величин.

2. Постройте график зависимости 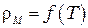и проанализируйте его. Выделите диапазон температур, в котором эта зависимость является линейной (при удачных измерениях линейность может наблюдаться во всём диапазоне), проведите прямую и на её продолжении при 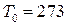К найдите соответствующее значение.

Далее пользуясь методом парных точек [2], найдите угловой коэффициент прямой, равный, как это следует из (2.2), 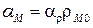. и температурный коэффициент сопротивления .

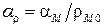При наличии программируемого калькулятора или компьютера можно использовать программу из [2] и найти и , а следовательно, и 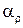, методом наименьших квадратов.

Задание 1

3. Постройте график зависимости 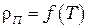и проведите усредненную кривую.

4. Постройте график зависимости 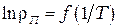и проанализируйте его. Согласно теории, он должен представлять прямую, разброс экспериментальных точек относительно которой должен носить случайный характер. Выделив такой линейный участок зависимости, проведите прямую и, взяв на этой прямой две произвольные точки, с помощью формулы (2.6) найдите значение .

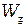Примечание: Конечно, для этой цели можно, как и в п.2, воспользоваться методом наименьших квадратов идя методом парных точек. Однако с целью ограничения объема вычислений можно ограничиваться указанной выше оценкой .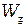

5. По формуле (8) найдите концентрацию электронов проводимости в металле. Для платины: плотность 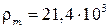кг/м³, молярная масса М = 195 кг/кмоль.

6. Используя формулы (4), (5) и экспериментальный результат по удельному сопротивлению металла при комнатной температуре, найдите подвижность электронов в металле. Сравните её с подвижностью электронов в типичных полупроводниках.

7. Используя оценку скорости теплового движения электронов в металле, оцените среднюю длину свободного пробега электронов в металле формул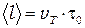е , где время релаксации, оценивается по подвижности 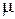с помощью формулы (24). Сравните 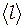с межатомным расстоянием в металле (2-3 А). Сделайте выводы по оценкам.

Контрольные вопросы

1. Проведите сравнительный анализ температурных зависимостей электрического сопротивления металлов и полупроводников. Как объясняются различия в характере этих зависимостей?

2. Почему, на ваш взгляд, рекомендуется проводить измерения сопротивлений металлического и полупроводникового образцов раздельно (одного при нагреве, другого при охлаждения)? Какие трудности встречаются в измерении температуры образца в этой установке?

3. При каких температурах можно ожидать заметных отклонений т линейности зависимосте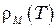й и 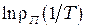и почему?

4. К дополнительному заданию: выполните оценку межатомных расстояний в металлическом образце (платине) при комнатной температуре.

Дата добавления: 2014-11-07