
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Интеграл. 2 страница
|
|
|
|
315. 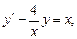
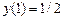 Коши есебін шешіңіз. Ж:
Коши есебін шешіңіз. Ж: 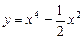
316. 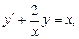
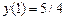 Коши есебін шешіңіз. Ж:
Коши есебін шешіңіз. Ж: 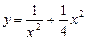
317. 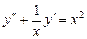 дифференциалдық теңдеуінің ретін төмендету үшін, қандай ауыстыруды қолданамыз. Ж:
дифференциалдық теңдеуінің ретін төмендету үшін, қандай ауыстыруды қолданамыз. Ж: 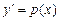 ,
, 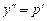
318. 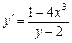 дифференциалдық теңдеуінің шешімін табыңыз. Ж:
дифференциалдық теңдеуінің шешімін табыңыз. Ж: 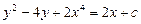
319. 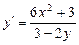 дифференциалдық теңдеуінің шешімін табыңыз. Ж:
дифференциалдық теңдеуінің шешімін табыңыз. Ж: 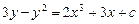
320.Бірінші ретті 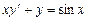 дифференциалдық теңдеуінің типін анықтаңыз. Ж: Бірінші ретті біртекті емес сызықты дифференциалдық теңдеу
дифференциалдық теңдеуінің типін анықтаңыз. Ж: Бірінші ретті біртекті емес сызықты дифференциалдық теңдеу
321.Бірінші ретті сызықтық теңдеу 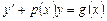 келесі ауыстыру арқылы шешіледі. Ж:
келесі ауыстыру арқылы шешіледі. Ж: 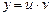
322. 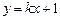 функциясы
функциясы 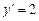 тедеуінің шешуі болатын к мәнін тап. Ж: 2
тедеуінің шешуі болатын к мәнін тап. Ж: 2
323. 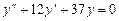 сызықтық біртекті дифференциалдық теңдеуінің жалпы шешімін табыңыз. Ж:
сызықтық біртекті дифференциалдық теңдеуінің жалпы шешімін табыңыз. Ж: 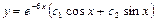
324. 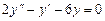 теңдеуінің жалпы шешімін табыңыз. Ж:
теңдеуінің жалпы шешімін табыңыз. Ж: 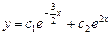
325. 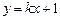 функциясы
функциясы 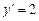 теңдеуінің шешуі болатын
теңдеуінің шешуі болатын  мәнін тап. Ж:
мәнін тап. Ж: 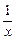
326. 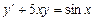 теңдеуіне сәйкес біртекті сызықты теңдеудің жалпы түбірін көрсетіңіз. Ж:
теңдеуіне сәйкес біртекті сызықты теңдеудің жалпы түбірін көрсетіңіз. Ж: 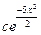
327. 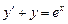 теңдеуіне қатысты біртекті сызықты теңдеудің жалпы түбірін көрсетіңіз. Ж:
теңдеуіне қатысты біртекті сызықты теңдеудің жалпы түбірін көрсетіңіз. Ж: 
328. 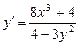 дифференциалдық теңдеуінің шешімін табыңыз. Ж:
дифференциалдық теңдеуінің шешімін табыңыз. Ж: 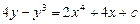
329. 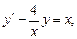
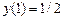 Коши есебін шешіңіз. Ж:
Коши есебін шешіңіз. Ж: 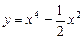
330.Бірінші ретті сызықтық дифференциалдық теңдеуді көрсетіңіз. Ж: 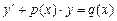
331. 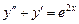 дифференциалдық теңдеуінің ретінтөмендету үшін, қандай ауыстыруды қолданамыз. Ж:
дифференциалдық теңдеуінің ретінтөмендету үшін, қандай ауыстыруды қолданамыз. Ж: 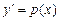 ,
, 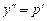
332. 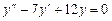 теңдеуінің жалпы шешімін табыңыз. Ж:
теңдеуінің жалпы шешімін табыңыз. Ж: 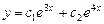
333. 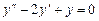 теңдеуінің жалпы шешімін табыңыз. Ж:
теңдеуінің жалпы шешімін табыңыз. Ж: 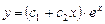
334. 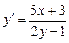 дифференциалдық теңдеуінің шешімін табыңыз. Ж:
дифференциалдық теңдеуінің шешімін табыңыз. Ж: 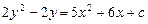
335. 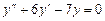 біртекті сызықты дифференциалдық теңдеудің жалпы түбірін табыңыз. Ж:
біртекті сызықты дифференциалдық теңдеудің жалпы түбірін табыңыз. Ж: 
336.Алғашқы шарт 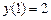 қанағаттандыратын
қанағаттандыратын 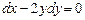 дифференциалдық теңдеуінің шешуін табыңыз. Ж:
дифференциалдық теңдеуінің шешуін табыңыз. Ж: 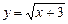
337. 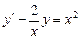 ,
, 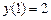 Коши есебін шешіңіз. Ж:
Коши есебін шешіңіз. Ж: 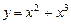
338.  түріндегі дифференциалдық теңдеудің атауы. Ж: біртекті
түріндегі дифференциалдық теңдеудің атауы. Ж: біртекті
339.Екінші ретті тұрақты коэффициентті сызықтық біртекті теңдеудің фундаментальды шешімдер жүйесінің 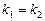 сипаттамалық теңдеудің бірдей түбірлері болған жағдайда берілуі. Ж:
сипаттамалық теңдеудің бірдей түбірлері болған жағдайда берілуі. Ж: 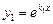 ,
, 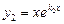
340.Берілгендердің арасындағы дифференциалдық теңдеу болатыны 1) 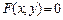 , 2)
, 2) 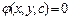 , 3)
, 3) 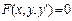 , 4)
, 4) 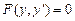 , 5)
, 5) 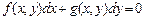 Ж: 3,4,5
Ж: 3,4,5
341. 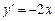 дифференциалдық теңдеуін шешіңіз. Ж:
дифференциалдық теңдеуін шешіңіз. Ж: 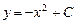
342. 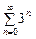 (1).
(1). 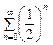 (2)
(2) 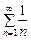 (3) қатарларының қайсысы жинақты қатар болады. Ж: 2
(3) қатарларының қайсысы жинақты қатар болады. Ж: 2
343.Дәрежелік қатардың
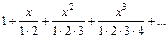 жалпы мүшесі келесі
жалпы мүшесі келесі
функция болады. Ж: 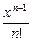
344.Дәрежелік қатардың 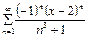 жалпы мүшесі келесі өрнек болады. Ж:
жалпы мүшесі келесі өрнек болады. Ж: 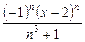
345.Дәрежелік қатарадың  жалпы мүшесі келесі өрнек болады. Ж:
жалпы мүшесі келесі өрнек болады. Ж: 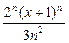
346. 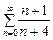 қатарының жинақтылығын зертеу үшін жинақтылықтың мынадай белгісін қолданамыз. Ж: Жинақтылықтың қажеттілік белгісі (жинақсыздықтың жеткілікті белгісі)
қатарының жинақтылығын зертеу үшін жинақтылықтың мынадай белгісін қолданамыз. Ж: Жинақтылықтың қажеттілік белгісі (жинақсыздықтың жеткілікті белгісі)
347.Гармоникалық қатардың түрі. Ж: 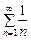
348. 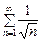 (1),
(1), 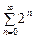 (2),
(2), 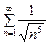 (3) қатарларының қайсысы жинақсыз қатар болатындығын көрсетіңіз. Ж: 1 және 2
(3) қатарларының қайсысы жинақсыз қатар болатындығын көрсетіңіз. Ж: 1 және 2
349. 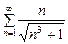 қатарының жинақтылығын зерттеу үшін мынадай белгіні қолданамыз. Ж: Салыстыру белгісі
қатарының жинақтылығын зерттеу үшін мынадай белгіні қолданамыз. Ж: Салыстыру белгісі
350. 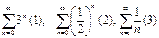 қатарларының қайсы-сы жинақты қатар. Ж: 2
қатарларының қайсы-сы жинақты қатар. Ж: 2
351. 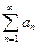 қатарының жинақтылығының қажетті шарты. Ж:
қатарының жинақтылығының қажетті шарты. Ж: 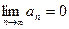
352.Дәрежелік қатардың 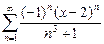 жалпы мүшесі келесі өрнек болады. Ж:
жалпы мүшесі келесі өрнек болады. Ж: 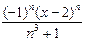
353.Дәрежелік қатардың 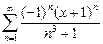 жалпы мүшесінің коэффициенті тең. Ж:
жалпы мүшесінің коэффициенті тең. Ж: 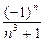
354.Дәрежелік қатардың 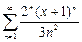 жалпы мүшесінің коэффициенті тең. Ж:
жалпы мүшесінің коэффициенті тең. Ж: 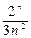
355.Дәрежелік қатардың
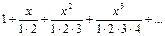 жалпы мүшесі келесі функция болады. Ж:
жалпы мүшесі келесі функция болады. Ж: 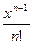
356. 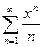 дәрежелік қатарының жинақтылық радиусы тең. Ж: 1
дәрежелік қатарының жинақтылық радиусы тең. Ж: 1
357.Дәрежелік қатардың 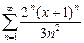 жалпы мүшесі келесі өрнек болады. Ж:
жалпы мүшесі келесі өрнек болады. Ж: 
358. 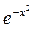 функциясын дәрежелік қатарға жіктеңіз. Ж:
функциясын дәрежелік қатарға жіктеңіз. Ж: 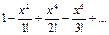
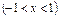 .
.
359. 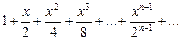 қатарының жинақтылық облысы. Ж:
қатарының жинақтылық облысы. Ж: 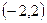
360. 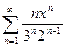 қатарының жинақтылық облысы. Ж:
қатарының жинақтылық облысы. Ж: 
361. 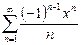 қатарының жинақтылық облысы. Ж:
қатарының жинақтылық облысы. Ж: 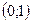
362.Нысанаға тигізу ықтималдығы 0,8. Нысанаға тигізе алмау ықтималдығын табыңыз. Ж: 0,2
363.Егер топта 9 студент болса, онда құрамында 3 ден топ активін неше әдіспен құруға болады. Ж: 84
364.Дискреттік кездейсоқ шаманың дисперсиясы тең болады. Ж: 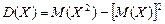
365.Ойын сүйегі лақтырылды. Үштен артық ұпай түсу ықтималдығын табыңыз. Ж: 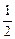
366.Үздіксіз кездейсоқ шаманың математикалық күтімі мынадай формуламен анықталады. Ж: 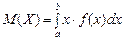
367.Қобдишадағы 20 электр шамының 15 – нің кернеуі 220в. Осы қобдишадағы электр шамдарын араластырып жіберіп алынған кез келген бір электр шамының кернеуінің 220в болатынды-ғының ықтималдығын табыңыз. Ж: 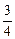
368.Қолдағы 5 папканы араластырып жіберіп неше әдіспен үшеуден әртүрлі папка алуға болады. Ж: 10
369.Студент 15 сұрақтың 6 біледі. Екі сұрақ қойғанда студенттің сынақ алу ықтималдығын табыңыз. Ж: 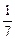
370.Атқыштың нысанаға тигізу ықтималдығы 0,7 болса, онда 2 рет атқанда кем дегенде бір рет тигізу ықтималдығын табыңыз. Ж: 0,91
371.Дүкенге сатып алушы ¼-тең ықтималдықпен зат сатып алады. Төрт адамның екеуі зат сатып алу ықтималдығын тап. Ж: 27/128
372.Егер топта 9 студент болса, онда құрамында 3 студенттен тұратын топ активтерін неше әдіспен құруға болады. Ж: 84
373.Дискретті кездейсоқ шама 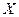 үлестіру заңы арқылы берілген
үлестіру заңы арқылы берілген 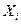 1 3 4 5
1 3 4 5 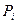 0,2 0,35 0,3
0,2 0,35 0,3 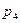 .
. 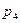 табыңыз. Ж: 0,15
табыңыз. Ж: 0,15
374.Үздіксіз кездейсоқ шаманың математикалық күтімі мынадай формуламен анықталады. Ж: 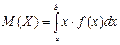
375.Үздіксіз кездейсоқ шама 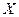 тығыздық үлестіру
тығыздық үлестіру 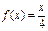 функциясы арқылы (0;4) аралығында берілген, одан тыс
функциясы арқылы (0;4) аралығында берілген, одан тыс 
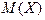 -ті табыңыз. Ж:
-ті табыңыз. Ж: 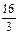
376.Қобдишадағы 12 қасықтың 6- күміс. Араластырып жіберіп алынған кез келген қасықтың күміс қасық екендігінің ықтималдығын табыңыз. Ж: 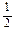
377.Бірінші атқыштың нысанаға тигізу ықтималдыңғы 0,6 ал екіншісінікі 0,8. Екі атқыштың да бірдей нысанаға тигізу ықтималдығын табыңыз. Ж: 0,48
378.Бір жылда екі фирманың банкрот болу ықтималдығы 0,06 және 0,09: Жылдың аяғында екі фирманың жұиыс істеп істеп тұру ықтималдығын тап. Ж: 0,8554
379. 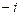 комплекстік саны мынадай тригонометриялық түрде жазылады. Ж:
комплекстік саны мынадай тригонометриялық түрде жазылады. Ж: 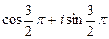
380. 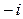 комплекстік саны мынандай көрсеткіштік түрде былай жазылады. Ж:
комплекстік саны мынандай көрсеткіштік түрде былай жазылады. Ж: 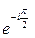
381. 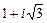 комплекстік саны мынадай тригонометриялық түрде жазылады. Ж:
комплекстік саны мынадай тригонометриялық түрде жазылады. Ж: 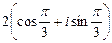
382. 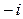 комплекстік саны мынандай көрсеткіштік түрде былай жазылады. Ж:
комплекстік саны мынандай көрсеткіштік түрде былай жазылады. Ж: 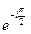
383. 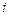 комплестік саны мынадай көрсеткіштік түрде былай жазылады. Ж:
комплестік саны мынадай көрсеткіштік түрде былай жазылады. Ж: 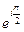
384. 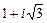 комплекстік саны мынадай тригонометриялық түрде жазылады. Ж:
комплекстік саны мынадай тригонометриялық түрде жазылады. Ж: 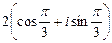
|
|
|
|
|
Дата добавления: 2014-11-07; Просмотров: 1183; Нарушение авторских прав?; Мы поможем в написании вашей работы!