Чем обуславливается парадокс Эрроу в процедуре группового выбора?

Групповой выбор

Основной проблемой группового выбора является проблема согласования индивидуального выбора.

Наиболее используемые процедуры согласования выбора:

1. простое большинство: 50%+1 голос;

2. квалифицированное большинство: 2/3 + 1 голос или ¾ + 1 голос;

3. подавляющее большинство: более 90%;

4. единогласное решение (консенсус, правило вето): решение принято только в том случае, если за него проголосовали все.

Не существует абсолютно справедливой процедуры группового выбора, которая всегда бы привела к решению, что показывает парадокс Эрроу. Коротко поясним его сущность.

Сформулируем достаточно очевидные предположения относительно группового выбора:

1. число выборщиков n ³ 2, число альтернатив m > 3. Первое из этих правил определяет, что выбор групповой. Второе говорит о том, что выбор не бинарный (из двух альтернатив);

2. условие монотонности - если альтернатива x принята большинством голосов, то добавление ещё одного голоса за эту альтернативу оставляет её принятой;

3. условие независимости несвязанных альтернатив – если альтернатива x_i принята, то повторное голосование по альтернативе x_j, не связанной с x_i, не меняет статус альтернативы x_i (она остается принятой);

4. условие автономности альтернатив - не существует альтернативы x_i, для которой любой набор выборщиков приводит к тому, что зта альтернатива принимается;

5. условие отсутствия диктаторства – принятие любой альтернативы x_i зависит от всех выборщиков в том смысле, что не существует выборщика R_i такого, что в независимости от голоса других выборщиков результат группового выбора всегда будет определяться выбором R_i.

Парадокс Эрроу состоит в том, что первые четыре принципа вступают в конфликт с пятым. Это говорит о том, что в любой демократической системе при принятии решения иногда бывает необходим диктатор.

Парадокс Эрроу демонстрирует, что наличие диктатора не является безусловно отрицательным требованием, т.к. отсутствие диктатора в ситуации группового выбора может привести к тому, что выбор не будет сделан. Многие процедуры голосования для избежания такой ситуации предлагают, что если демократический групповой выбор не приводит к решению, то решение может приниматься специальной группой лиц или одним лицом.

Основной причиной этого является отсутствие свойства транзитивности в отношении доминирования или, как его часто называют, в мажоритарном отношении. Предположим, что принятие решения связано с распределением какого-то ресурса 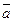={a₁,..,a_n}, причем ресурс a =. Назовём соответствующее распределение ресурса = {b₁,..,b_n} хуже, чем a, для какого-то выборщика R_i, если a_i>b_i, а для всех остальных участников a_j £ b_j j¹i. Отметим, что по любому правилу большинства будет принята альтернатива b, поскольку она не ухудшает ничей ресурс, кроме одного R_i. Оказывается, что если есть два произвольных распределения ресурса a и b, то всегда существует тоталитарно-мажоритарный путь (процедура голосования), позволяющий распределить ресурс a в пользу b.

Ещё более сложной является ситуация группового выбора, допускающая возможность существования коалиции. Парадокс коалиционного выбора состоит в том, что правильная организация коалиции в процедуре многошагового выбора позволяет в итоге принять альтернативу, которая изначально поддерживалась меньшинством выборщиков. При этом на каждом шаге принципом согласования индивидуальных выборов является принцип большинства. Это подтверждает ситуация коалиционного многошагового выбора, приведенная на нижеследующем рисунке.

Видно, что в конечном счете принятая альтернатива поддерживалась на начальном этапе меньшинством голосов (8 из 27). Даже на втором этапе эту альтернативу поддерживало меньшинство (4 из 9). Но правильно организованная коалиция позволила принять ее на последнем этапе.

Существуют ли в демократической системе альтернатива диктатору? Здесь можно рекомендовать следующие два подхода.

В последнее время каждый групповой выбор, приводящий к некоторой парадоксальной ситуации, рекомендуют интерпретировать как опрос некоторой экспертной группы. Сам статус эксперта говорит о том, что это лицо только готовит решение, но отнюдь не принимает его. Поэтому, если лиц, принимающих решения, нельзя ранжировать, то экспертов ранжировать можно. Таким образом, задавая приоритеты для мнения отдельных экспертов, фактически можно ввести того же самого диктатора.

Другой подход часто называют методом Делфи. Он предполагает, что между лицами, принимающими решения, всегда можно установить консенсус, если путём многократных обсуждений и голосования отбросить из альтернатив всё то, что не устраивает отдельных участников процедуры принятия решения. Принципиальная достижимость консенсуса основана на том, что каждое лицо действует рационально.

Реальный процесс выбора, к сожалению, достаточно часто происходит либо на нерациональных основаниях, либо эта рациональность гораздо шире, чем рациональность отдельного акта выбора.

Дата добавления: 2014-10-15