Реляционное исчисление кортежей и доменов

В то время как реляционная алгебра использует в качестве операндов отношения, реляционное исчисление кортежей строит свои выражения над переменными, принимающими значения кортежей (переменные-кортежи). Выражения реляционного исчисления кортежей имеют вид:

,

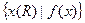где f-формула, выражающая некоторый предикат над переменной-кортежем x. Результат этого выражения есть отношение r(R),которое состоит из всех кортежей t(R), для которых f(t) истинно.

Минимальные строительные блоки для формул называют атомами. Атомы бывают следующих типов:

1. Атом xÎ R или R(x), где x – кортеж отношения R;

2. Атом S(i) q U(j), где S и U – переменные-кортежи; q - оператор сравнения; i, j – номера или имена атрибутов в соответствующих кортежах.

3. Атом S(i) q а или, а q S(i), где, а – константа, S – переменная-кортеж; q - оператор сравнения; i – номер или имя атрибута в соответствующем кортеже.

4. Операции: сравнения (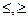,<,>,=,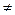), кванторы всеобщности(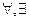), логические операции().

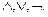5. Скобки.

В реляционном исчислении с переменными – кортежами справедливо следующее утверждение: для любого выражения реляционной алгебры существует эквивалентное ему безопасное выражение в реляционном исчислении с переменными-кортежами. В исчислении кортежей на вид формул накладываются определенные ограничения, чтобы исключить выражения, не имеющие смысла. Формулы, удовлетворяющие этим ограничениям, называют разрешёнными формулами, а соответствующие выражения – безопасными.

Реляционное исчисление доменов напоминает реляционное исчисление кортежей, за тем исключением, что переменные этого исчисления являются переменными значениями из доменов, а не переменными-кортежами. Выражение исчисления доменов имеет вид:

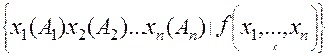
где f – формула, обладающая тем свойством, что ее переменные являются переменными значениями из доменов.

Формула состоит из следующих атомов:

1. Атом R(a₁,…,a_k), где 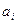- либо переменная исчисления доменов, либо постоянная из домена, с помощью которого задается атрибут.

2. Атом x q y, где x, y – константы или переменные на домене; q - оператор сравнения.

3. Формула использует кванторы "x; $x и логические операции Ù, Ú, ù.

4. Скобки.

В реляционном исчислении с переменными на доменах справедливы следующие утверждения:

1. Для каждого безопасного выражения реляционного исчисления с переменными кортежами существует эквивалентное ему безопасное выражение реляционного исчисления с переменными на доменах.

2. Для каждого безопасного выражения реляционного исчисления с переменными на доменах существует эквивалентное ему выражение реляционной алгебры.

Дата добавления: 2014-10-15