Краткая теория. Цель работы: изучение свойств вязкой жидкости и ознакомление с методом Стокса, экспериментальное определение коэффициента вязкости глицерина

МЕТОДОМ СТОКСА

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ЖИДКОСТИ

Цель работы: изучение свойств вязкой жидкости и ознакомление с методом Стокса, экспериментальное определение коэффициента вязкости глицерина.

Приборы и принадлежности: стеклянный цилиндр с глицерином, шарик малого диаметра, микрометр, секундомер, пинцет, масштабная линейка.

Внутренним трением (вязкостью) называется явление возникновения сил, препятствующих относительному перемещению слоев жидкости или газа. Жидкость, обладающая внутренним трением, называется вязкой.

Основной закон вязкого течения был установлен Ньютоном:

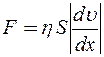, (1)

где сила внутреннего трения F – тангенциальная (касательная) сила, направленная вдоль соприкасающихся слоев и вызывающая сдвиг слоев жидкости (газа) друг относительно друга; S – площадь соприкосновения движущихся слоев; - градиент скорости, равный изменению скорости движения слоев на единицу длины dx в направлении, перпендикулярном направлению движения слоев (характеризует быстроту изменения скорости от слоя к слою) (рис. 1).

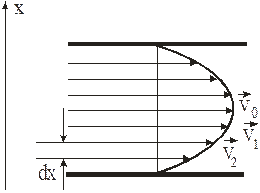Рис. 1. Распределение скоростей слоев вдоль сечения трубы медленно текущей вязкой жидкости

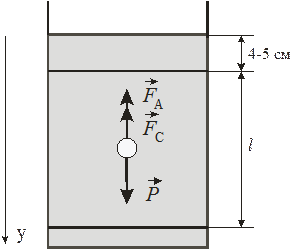Рис. 2. Силы, действующие на падающий в жидкости шарик

Величина η называется коэффициентом внутреннего трения или коэффициентом динамической вязкости и характеризует сопротивление жидкости (газа) смещению ее слоев. Коэффициент вязкости η есть физическая величина, численно равная силе внутреннего трения, действующей на единицу площади S соприкасающихся слоев при градиенте скорости, равном единице:

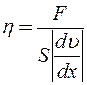. (2)

В системе СИ единица измерения коэффициента вязкости [ η ] = 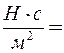Па·с.

Величина φ = 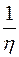называется текучестью.

Внутреннее трение является одним из явлений переноса. Явления переноса состоят в возникновении направленного переноса физической величины: массы (диффузия), внутренней энергии (теплопроводность) или импульса (внутреннее трение) при наличии пространственных неоднородностей этой величины в системе. Перенос физической величины происходит в направлении, обратном его градиенту, что приближает систему к равновесному состоянию (при котором средние значения всех величин, характеризующих состояние, не зависят от времени).

Внутреннее трение в жидкостях и газах обусловлено переносом импульса молекул при тепловом движении из слоя, движущегося с большей скоростью, в слой, движущийся с меньшей скоростью, что приводит к замедлению быстрее движущегося слоя и ускорению медленнее движущегося слоя. Значения коэффициента вязкости жидкостей на несколько порядков больше, чем для газов из-за существенно больших сил взаимодействия между молекулами жидкости по сравнению с газами. Коэффициент вязкости жидкостей зависит от рода жидкости и уменьшается с повышением температуры и ростом давления. Коэффициент вязкости газов увеличивается при повышении температуры пропорционально и не зависит от давления.

Коэффициент вязкости может быть определен методом падающего шарика в вязкой среде - методом Стокса. Рассмотрим падение шарика в вязкой покоящейся жидкости. На шарик массой т и радиусом r, падающий со скоростью 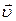в жидкости с вязкостью h действуют три силы: сила тяжести 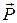, выталкивающая сила 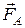, сила сопротивления 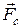(рис. 2).

Сила тяжести равна 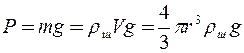, (3)

где ρ _ш– плотность шарика; V – объем шарика; r – радиус шарика; g – ускорение силы тяжести.

Выталкивающая сила определяется по закону Архимеда: на тело, погруженное в жидкость (газ), действует со стороны этой жидкости (газа) выталкивающая сила, равная весу вытесненной телом жидкости (газа), направленная по вертикали вверх и приложенная к центру тяжести вытесненного объема:

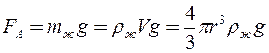, (4) где m_ж – масса вытесненной шариком жидкости; ρ _ж - плотность жидкости.

Сила сопротивления 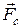движению, обусловленная силами внутреннего трения между слоями жидкости, зависит от скорости движения тела, его размеров и формы. Как установил Стокс, для тел шарообразной формы, движущихся с небольшой скоростью, модуль силы сопротивления жидкости F_с пропорционален скорости движения υ, радиусу шара r и коэффициенту вязкости жидкости h:

. (5)

Подчеркнём, что здесь играет роль не трение шарика о жидкость, а трение отдельных слоев жидкости друг о друга, так как при соприкосновении твёрдого тела с жидкостью к поверхности тела тотчас же прилипают молекулы жидкости. Тело обволакивается слоями жидкости и связано с ними молекулярными силами. Непосредственно прилегающий к телу слой жидкости движется вместе с телом со скоростью движения тела. Этот слой увлекает в своём движении соседние слои жидкости, которые на некоторый период времени приходят в плавное движение.

Формула Стокса применима также и к случаю падения дождевых капель в атмосфере.

Уравнение динамики для движущегося в жидкости шарика имеет вид

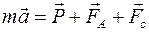(6)

а в проекции на ось у: ma= P-F_A -F_C.

Так как силы Р и F_А постоянны, а сила F_С возрастает с увеличением скорости движения шарика, то с некоторого момента времени эти силы уравновесят друг друга, т. е. равнодействующая всех сил станет равной нулю: P-F_A -F_C = 0, и, следовательно, с этого момента времени шарик будет двигаться равномерно. Тогда

P = F_А+F_С (7)

и 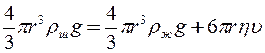, (8)

откуда

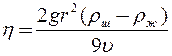. (9)

Т.к. скорость равномерного движения шарика в жидкости определяется по формуле 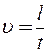, где t – время, за которое шарик прошел расстояние l, а радиус шарика r равен половине его диаметра D, то получим окончательное выражение для коэффициента вязкости жидкости

.

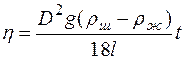(10)

Экспериментальная установка состоит из стеклянного цилиндра, наполненного исследуемой жидкостью (рис. 2). На цилиндре имеются две горизонтальные кольцевые метки, расположенные друг от друга на расстоянии l. В эксперименте определяется время прохождения шариком расстояния l между этими метками.

Дата добавления: 2014-10-15