Динамика популяций

Динамика популяций — это процессы изменения ее основных биологических показателей (численности, биомассы, структуры) во времени в зависимости от экологических факторов. Жизнь популяции проявляется в ее динамике — одном из наиболее значимых биологических и экологических явлений.

Кривые выживания. Кривая выживания представляет собой график зависимости от времени числа выживших на данный момент особей для некоторой начальной группы новорожденных. Каждому биологическому виду свойственна своя характерная кривая выживания (рис. 6.5).

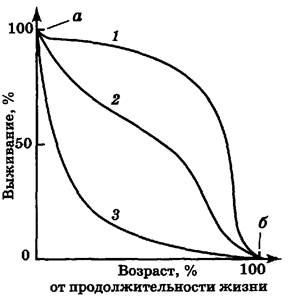
Рис. 6.5. Кривые выживания:

1 - человек или крупные млекопитающие; 2 - гидра или чернохвостый олень; 3 - устрица или рыба

Все животные и растения подвержены старению, которое проявляется в снижении жизненной активности с возрастом после периода зрелости. Непосредственные причины смерти могут быть разными, но в основе их лежит уменьшение сопротивляемости организма к неблагоприятным факторам, например к болезням.

Кривая 1 на рис. 6.5 близка к идеальной кривой выживания для популяции, в которой старение — главный фактор, влияющий на смертность. Так, в современной развитой стране с высоким уровнем медицинского обслуживания и рациональным питанием большинство людей доживает до старости, но среднюю ожидаемую продолжительность жизни почти невозможно увеличить более чем до 75 лет. Поскольку даже в наиболее высокоразвитых странах детская смертность выше средней, она изображается начальным участком а, а наличие долгожителей — конечным участком б (кривая 1). Кроме того, на кривую выживания влияет фактор «случайной гибели», причины которой с возрастом могут меняться. Например, в Англии наибольшая смертность в результате автомобильных аварий приходится на возраст 20—25 лет.

Закономерность, аналогичная кривой 1 свойственна и однолетним растениям, например злаковым, ибо на поле все растения одного вида стареют одновременно.

Кривая 3 иллюстрирует изменения в популяции, у которой смертность относительно постоянна в течение всей жизни организмов (например, 50 % за определенное время). Причиной смерти преимущественно служит случай, и особи гибнут до начала заметного старения. Кривая, подобная этой, была получена, например, для «популяции» стеклянных (легко бьющихся) стаканов в кафе. В природе к таким видам относятся, например, устрицы, дающие огромное потомство, а также растения, размножающиеся благодаря рассеиванию большого числа семян. Большая или меньшая смертность среди молодых особей приводит к изменению крутизны опускания начальной части кривой 3.

К промежуточному типу относят кривые выживания таких видов, для которых смертность мало меняется с возрастом. В природе существует много видов птиц, ящериц, мелких млекопитающих и других организмов, имеющих кривые выживания 2, которые отличаются от прямолинейной диагонали некоторой выпуклостью (вогнутостью) или волнообразностью.

Форма кривой выживания часто меняется при изменении плотности популяции. С увеличением плотности кривая становится более вогнутой, т. е. при увеличении численности организмов их смертность возрастает.

Знание типа кривой выживания дает возможность построить пирамиду возрастов (рис. 6.6). Следует различать три типа таких пирамид. Пирамида с широким основанием, что соответствует высокому проценту молодняка, характерна для популяции с большим значением коэффициента рождаемости. Средний тип пирамиды соответствует равномерному распределению особей по возрастам в популяции со сбалансированными коэффициентами рождаемости и смертности — пирамида выровненная. Пирамида с узким основанием (обращенная), отвечающая популяции с численным преобладанием старых особей над молодняком, характерна для сокращающихся популяций. В таких популяциях коэффициент смертности превышает коэффициент рождаемости.

Важным фактором изменения численности популяций является соотношение полов. Оно редко бывает равным единице, так как в большинстве случаев один из полов преобладает над другим. У позвоночных часто при рождении самцов бывает несколько больше, чем самок. У утиных самцы тоже нередко численно превалируют над самками. Зато в крупных популяциях белок доминируют самки (рис. 6.6).

Рис. 6.6. Пирамида возрастов оленей (из Рамада, 1981):

1 —классическое изображение, 2— более сложное изображение с учетом погибших особей в каждом классе, символически представленных силуэтами черепов

Рост популяции и кривые роста. Если при незначительной эмиграции и иммиграции рождаемость превышает смертность, то популяция будет расти. Рост популяции является непрерывным процессом, если в ней существуют все возрастные группы. Скорость роста популяции при отсутствии каких-либо экологических ограничений описывает дифференциальное уравнение

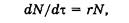
где N — численность особей в популяции; t — время; r — константа скорости естественного прироста.

J-образная модель роста популяции. Если r > 0, то со временем численность популяции становится больше. Рост происходит сначала медленно, а затем стремительно увеличивается по экспоненциальному закону, т. е. кривая роста популяции принимает J-образный вид (рис. 6.7, а).Такая модель основывается на допущении, что рост популяции не зависит от ее плотности. Считают, что почти любой вид теоретически способен увеличить свою численность до заселения всей Земли при достатке пищи, воды, пространства, постоянстве условий среды и отсутствии хищников. Эта идея была выдвинута еще на рубеже XVIII и XIX вв. английским экономистом Томасом Р. Мальтусом, основоположником теории мальтузианства.

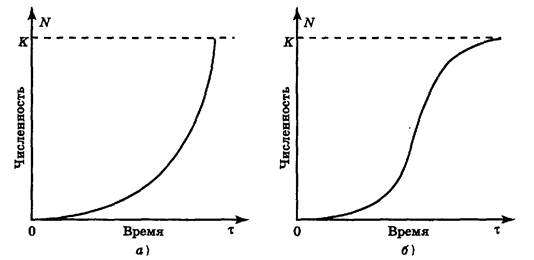
Рис. 6.7. Типы кривых роста численности популяции (модели роста

популяции):

а — J-образная; б — S-образная; К — поддерживающая емкость среды.

S-образная модель роста популяции. Иное развитие получает ситуация при ограниченности пищевых ресурсов либо при накоплении токсичных продуктов (отходов) метаболизма. Первоначальный экспоненциальный рост в исходных благоприятных условиях со временем продолжаться не может и постепенно замедляется. Плотность популяции регулирует истощение пищевых ресурсов, накопление токсикантов и поэтому влияет на рост численности. С увеличением плотности скорость роста популяции постепенно снижается до нуля и кривая выходит на некоторый стабильный уровень (график образует плато). Кривая такого роста (рис. 6.7, б) имеет S-образную форму, и поэтому соответствующая модель развития событий называется S -образной. Она характерна, например, для дрожжей, фактором, ограничивающим их рост, является накопление спирта, а также для водорослей, самозатеняющих друг друга. В обоих случаях численность популяции не достигает уровня, на котором начинает сказываться нехватка элементов питания (биогенов).

На рост численности, в которой значительную (возможно, даже главную) роль играет пространство, также влияет перенаселенность. Лабораторные опыты с крысами показали, что по достижении определенной плотности популяции плодовитость животных резко снижается даже при избытке пищи. Возникают гормональные сдвиги, влияющие на половое поведение; чаще встречается бесплодие, поедание детенышей родителями и т. п. Резко ослабевает родительская забота о потомстве, детеныши раньше покидают гнездо, в результате чего снижается вероятность их выживания. Усиливается агрессивность животных. Подобные явления встречаются также в популяциях ряда млекопитающих, причем не только в лабораторных, но и природных условиях.

Скорость роста численности в S-образной модели определяет дифференциальное уравнение

где К — поддерживающая емкость среды, т. е. максимальный размер популяции, которая может существовать в данных условиях, удовлетворяя свои потребности неопределенно долго.

Если N > К, скорость роста отрицательна. Если N < К, скорость роста положительна и величина популяции N стремится к К, т. е. приводится в соответствие с поддерживающей емкостью среды. Если N = К, скорость роста популяции равна нулю. При нулевом росте популяция стабильна, т. е. ее размеры не меняются, хотя отдельные организмы по-прежнему растут, размножаются и отмирают. Происходящее размножение уравновешивается смертностью.

В специализированной литературе J и S - образные модели роста численности часто называют соответственно экспоненциальной и логистической.

Поддерживающая емкость играет решающую роль не только при росте популяции по S-образной, но также и по J-образной модели, ибо в некоторый момент времени все же наступает исчерпание какого-либо ресурса среды, т. е. он (или даже несколько одновременно) становится лимитирующим.

Развитие дальнейших событий показано на рис. 6.8, а, б. После бума с внезапным выходом J-образной кривой за пределы уровня К происходит крах популяции, т. е. катастрофа, приводящая к резкому снижению численности. Поэтому в иностранной литературе S-образная модель называется моделью типа «бум — крах».

Причиной краха часто бывает внезапное резкое изменение условий окружающей среды (экологических факторов), понижающее поддерживающую емкость среды. Тогда огромное число особей, не способных эмигрировать, погибает.

При наиболее благоприятном для популяции стечении обстоятельств новый уровень численности соответствует поддерживающей емкости среды или, иначе говоря, кривая роста превращается из J-образной в S-образную (рис. 6.8).

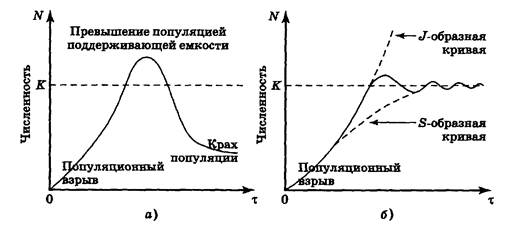
Рис. 6.8. Варианты завершения роста популяции по J-образной модели:

а — для дафнии на питательной среде; б — преобразование в

S-образный вид

Однако исчерпание пищевых ресурсов может привести также к появлению и других трудностей для популяции, например к развитию болезней. Тогда численность снижается до уровня значительно более низкого, чем поддерживающая емкость среды, а в пределе популяция может даже быть обречена на вымирание.

Для S-образной модели в случаях отставания действия регулирующих механизмов по каким-либо причинам, например в связи с затратами времени на воспроизводство или по иным причинам, временное запаздывание учитывает дифференциальное уравнение

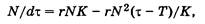
где Т — время, необходимое системе для реакции на внешнее воздействие.

Вычитаемое в правой части уравнения, содержащее N², позволяет предсказать момент выхода системы из состояния равновесия в случаях, когда время запаздывания относительно велико по сравнению с временем релаксации (1 /r) системы.

В итоге при увеличении в системе времени запаздывания вместо асимптотического приближения к состоянию равновесия происходит колебание численности организмов относительно теоретической S-образной кривой. В случаях, когда пищевые ресурсы ограничены, популяция не достигает устойчивого равновесия, ибо численность одного поколения зависит от численности другого, что отражается на скорости репродукции и приводит к хищничеству и каннибализму. Колебания численности популяции, для которой характерны большие значения r, малое время воспроизводства t и несложный регулирующий механизм могут быть весьма значительными.

Описанные модели роста популяции и дифференциальные уравнения предполагают, что все организмы сходны между собой, имеют равную вероятность погибнуть и равную способность к размножению, так что скорость роста популяции в экспоненциальной фазе зависит только от ее численности и не ограничена условиями среды, которые остаются постоянными. Они точно описывают процессы роста и взаимодействия особей в большинстве искусственных и некоторых естественных популяциях. «Идеальность» всех экологических факторов в исходных условиях предопределила то, что рассматриваемые модели называют идеальными.

Для природных популяций принятые допущения чаще всего неверны. В естественных условиях J и S-образные модели роста популяции преимущественно можно наблюдать в случаях, когда тех или иных животных вселяют или они сами распространяются в новые для них районы. Тем не менее теоретические модели роста позволяют лучше понять процессы, происходящие в естественных условиях. Большинство принципов, используемых для моделирования популяций животных, применимо также и для моделирования популяций растений.

Следует отметить, что при любой модели (как J, так и S-образной) вначале характерна фаза экспоненциального роста численности популяции (рис. 6.5, 6.6, б). Поэтому при сочетании благоприятных (оптимальных) значений всех факторов среды возникает «популяционный взрыв», т. е. особо быстрый рост популяции того или иного вида.

Миграция или расселение также, как и внезапное снижение скорости размножения, могут способствовать уменьшению численности популяции. Расселение может быть связано с определенной стадией жизненного цикла, например с образованием семян.

Применительно к условиям реальной природной среды принято использовать понятия биотический потенциал — совокупность всех экологических факторов, способствующих увеличению численности популяции, или видовая способность к размножению при отсутствии ограничений со стороны среды, а также сопротивление среды — сочетание факторов, ограничивающих рост (лимитирующих факторов). Подводя итог, можно сказать так: "Любые изменения популяции есть результат нарушения равновесия между ее биотическим потенциалом и сопротивлением окружающей среды".

Дата добавления: 2014-10-15