Преобразование чисел из одной системы счисления в другую

Так как десятичная система для нас удобна и привычна, все арифметические действия мы делаем в ней, и преобразование чисел из произвольной недесятичной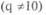системы в десятичную удобно выполнять на основе разложения по степеням q, например:

11100111₍₂₎= 1 х 2⁷ + 1 х 2⁶ + 1 х 2⁵ + 0 х 2⁴ + 0 х 2³ + 1 х 2² + + 1 х 2¹ + 1 х 2° = 128 + 64 + 32 + 4 + 2 + 1 = 231₍₁₀₎,

или 347 =3х8²+4х8' + 7x8° =3x64+ 4x8 + 7 = 231

Преобразование из десятичной в прочие системы счисления проводится с помощью правил умножения и деления. При этом целая и дробная части переводятся отдельно.

Рассмотрим алгоритм на примере перевода десятичного числа 231 в двоичную систему (совершенно аналогичен перевод из десятичной системы в любую q-ичную).

Разделим число на два (основание системы): нацело 231: 2 = 115 и остаток 1, т.е. можно записать 231 = 115x2'+ 1 х2°.

Число 115 (такой двоичной цифры нет) тоже может быть разделено нацело на 2, т.е. 115: 2 = 57 и остаток 1. По аналогии запишем

231= (57x2 + 1) х 2 + 1 = 57х2²+ 1 х 1'+ 1 х 2⁰;

аналогично продолжим процесс дальше:

57: 2 = 28, остаток 1; 231 = ((28 х 2 + 1) х 2 + 1) х 2 + 1 = 28 х x2³ + 1 х 2² + 1 х 2¹ + 1 х 2°.

28: 2 = 14, остаток 0; 231 = (((14 х 2 + 0) х 2 +1) х 2 + 1) х 2 + 1 14 х 2⁴+ 1 х2²+ 1 х2'+ 1 х2°.

14:2 = 7, остаток 0; 231=((((7 х 2 + 0) х 2 + 0) х 2 + 1) х 2 + 1)х к 2 + 1 = 7 х 2⁵ + 1 х 2² + 1 х 2'+ 1 х 2°.

7:2 = 3, остаток 1; 231 = (((((3 х2 + 1)х2 + 0)х2 + 0)х2 + I I) х 2 + 1) х 2 + 1 = 3 х 2⁶ + 1 х 2⁵ + 1 х 2² + 1 х 2¹ + 1 х 2°.

3:2=1; остаток 1; далее процесс продолжать нельзя, так как 1 не делится нацело на 2.

231 = ((((((1 х2+1)х2+1)х2 + 0)х2 + 0)х2+1)х2+1)х X 2 + 1 = 1 х 2⁷ + 1 х 2⁶ + 1 х 2⁵ + 1 х 2² + 1 х 2' + 1 х 2°.

Таким образом, последовательное деление нацело позволяет разложить число по степеням двойки, а это в краткой записи и есть двоичное изображение числа.

231 = 1 х2⁷+ 1 х2⁶+ 1 х2⁵+ 0х2⁴+0х2³+ 1 х2²+ 1 х2' + l 1x2°= 11100111₍₂₎.

Эти выкладки можно сократить, записав процесс деления следующим образом:

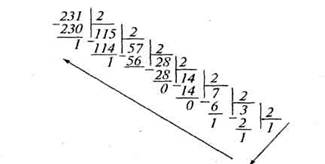
231₍₁₀₎=11100111₍₂₎

Читая частное и остатки от деления в порядке, обратном получению, получим двоичную запись числа. Такой способ перевода чисел называется правилом (алгоритмом) последовательного деления, очевидно, что он применим для любого основания.

Между двоичной системой счисления, с одной стороны, и восьмеричной и шестнадцатеричной (заметим 8 и 16 — есть третья и четвертая степени двойки) - с другой, существует связь, позволяющая легко переводить числа из одной системы в другую. Рассмотрим ид примере:

231 ₍₁₀₎= 11100111 ₍₂₎= 1 х 2⁷+ 1 х 2⁶ + 1 х 2⁵ + 1 х 2² + 1 х 2¹ + 1 х 2⁰

Для перевода в шестнадцатеричную систему счисления сгруппируем группы по четыре члена и вынесем в каждой группе за скобки множители, кратные. 2⁴. Получим:

(1 х 2³ + 1 х 2² + 1 х 2¹ + 0 х 2°) х 2⁴ + (0 х 2³ + 1 х 2² + 1 х 2¹ + 1 х 2°) =

=(1 х 2³ + 1 х 2² + 1 х 2¹ + 0) х 16¹ + (0+1 х 2² + 1 х 2¹ + 1 х 2°) х 16° =

=14 х 16¹ + 7 х 16° = E7₍₁₆₎ =

=231

Заключаем: для того, чтобы перевести число из двоичной системы в шестнадцатеричную, надо выделить группы по четыре цифры (они называются тетрадами), и каждую группу независимо от других перевести в одну шестнадцатеричную цифру.

Дата добавления: 2014-10-15