В закрытых системах

Термодинамические процессы идеальных газов

ЛЕКЦИЯ 5

Основными процессами, весьма важ­ными и в теоретическом, и в прикладном отношениях, являются: изохорный, протекающий при постоянном объеме; изобарный, протекающий при посто­янном давлении; изотермический, происходящий при постоянной темпера­туре; адиабатный — процесс, при ко­тором отсутствует теплообмен с окружа­ющей средой, и политропный, удов­летворяющий уравнению .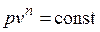

Метод исследования процессов, не зависящий от их особенностей и являю­щийся общим, состоит в следующем:

выводится уравнение процесса, уста­навливающее связь между начальными и конечными параметрами рабочего тела в данном процессе;

вычисляется работа изменения объема газа;

определяется количество теплоты, подведенной (или отведенной) к газу в процессе;

определяется изменение внутренней энергии системы в процессе;

определяется изменение энтропии системы в процессе.

Изохорный процесс. При изохорном процессе выполняется условие

dv = 0 или v = const. Из уравнения состояния иде­ального газа следует, что p/T=R/v= const, т. е. давление газа прямо пропорционально его абсолютной темпе­ратуре:

.

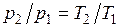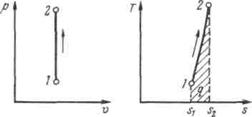
Рисунок 5.1 - Изображение изохорного процесса в р,v- и T, s -координатах

Работа расширения в этом процессе равна нулю, так как dv= 0.

Количество теплоты, подведенной к рабочему телу в процессе 12 при 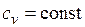, определяется как:

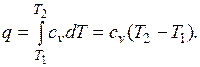
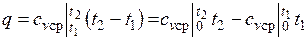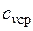При переменной теплоемкости , где — средняя массовая изохорная теплоемкость в интервале темпера­тур от t 1 до t 2.

Так как 1= 0, то в соответствии с пер­вым законом термодинамик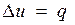и и

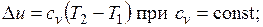
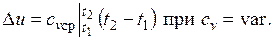
Поскольку внутренняя энергия идеально­го газа является функцией только его температуры, то полученные формулы справед­ливы для любого термодинамического процесса идеального газа.

Изменение энтропии в изохорном процессе определяется по формуле

,

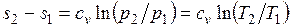т. е. зависимость энтропии от температу­ры на изохоре при с_v = const имеет лога­рифмический характер.

Изобарный процесс. Из уравнения состояния идеального газа при р =const находим 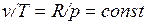, или 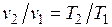, т. е. в изобарном процессе объем газа пропорционален его абсолютной темпе­ратуре (закон Гей-Люссака, 1802 г.). На рисунке изображен график процесса.

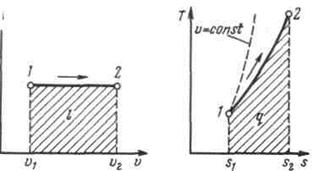
Рисунок 5.2 - Изображение изобарного процесса в p,v - и T,s -координатах

Из выражения 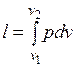следует, что .

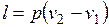Так как 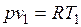и 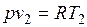, то одно­временно

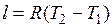
Количество теплоты, сообщаемое га­зу при нагревании (или отдаваемое им при охлаждении):

,

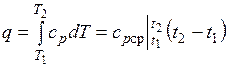где 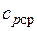— средняя массовая изобарная теплоемкость в интервале темпера­тур от t 1до t 2при 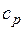= const

.

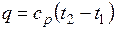Изменение энтропии при с_р = const согласно равно

,

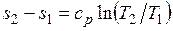т. е. температурная зависимость энтро­пии при изобарном процессе тоже имеет логарифмический характер, но поскольку с_р>с_v, то изобара в Т, s-диаграмме идет более полого, чем изохора.

Изотермический процесс. При изотер­мическом процессе температура постоян­на, следовательно, pv = RT = const, или

,

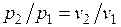т. е. давление и объем обратно пропорци­ональны друг другу, так что при изо­термическом сжатии давление газа воз­растает, а при расширении — падает (закон Бойля — Мариотта, 1662 г.).

Графиком изотермического процесса в р,v –координатах является равнобокая гипербола, для которой координатные оси служат асимптотами.

Работа процесса:

.

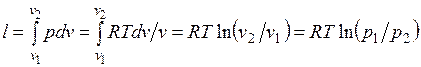Так как температура не меняется, то внутренняя энергия идеального газа в данном процессе остается постоянной (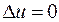) и вся подводимая к газу тепло­та полностью превращается в работу расширения:

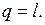
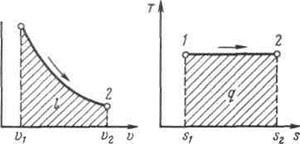
Рисунок 5.3 - Изображение изотермического про­цесса в р, v- и T, s -координатах.

При изотермическом сжатии от газа от­водится теплота в количестве, равном затраченной на сжатие работе.

Изменение энтропии в изотермиче­ском процессе выражается формулой

.

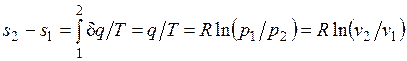Адиабатный процесс. Процесс, про­исходящий без теплообмена с окружаю­щей средой, называется адиабатным, т. е.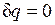. Для того чтобы осуществить та­кой процесс, следует либо теплоизолиро­вать газ, т. е. поместить его в адиабат­ную оболочку, либо провести процесс на­столько быстро, чтобы изменение темпе­ратуры газа, обусловленное его тепло­обменом с окружающей средой, было пренебрежимо мало по сравнению с из­менением температуры, вызванным рас­ширением или сжатием газа. Как прави­ло, это возможно, ибо теплообмен про­исходит значительно медленнее, чем сжатие или расширение газа.

Уравнения первого закона термоди­намика для адиабатного процесса прини­мают вид: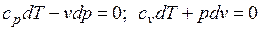. Поделив первое уравнение на второе, получим

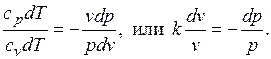
Интегрируя последнее уравнение при условии, что k =c_p/c_v= const, находим

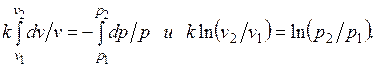
После потенцирования имеем

. *

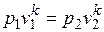Это и есть уравнения адиабаты идеаль­ного газа при постоянном отношении теплоемкостей (k = const). Величина

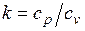
называется показателем адиаба­ты. Подставив c_p = c_v-R, получим k. Согласно классической кине­тической теории теплоемкость газов не зависит от температуры, по­этому можно считать, что величина k также не зависит от температуры и оп­ределяется числом степеней свободы мо­лекулы. Для одноатомного газа k =1,66 для двухатомного k =1,4, для трех- и многоатомных газов k =l,33.

Поскольку k> 1, то в координатах р, v линия адиабаты идет круче линии изотермы: при адиабатном расши­рении давление понижается быстрее, чем при изотермическом, так как в процессе расширения уменьшается температура газа.

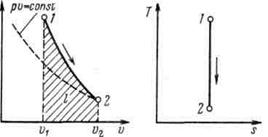
Рисунок 5.4 - Изображение адиабатного процесса в р, v- и Т, s-координатах

Определив из уравнения состояния, написанного для состояний 1 и 2, отно­шение объемов или давлений, получим уравнение адиабатного процесса в форме, выражающей зависимость температуры от объема или давления:

;

.

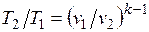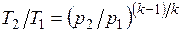Работа расширения при адиабатном процессе согласно первому закону термодинамики совершается за счет уменьшения внутренней энергии и может быть вычислена по одной из следующих формул:

.

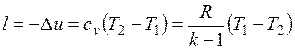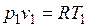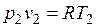Так как и , то

.

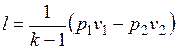В данном процессе теплообмен газа с окружающей средой исключается, по­этому q=0. Выражение 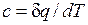пока­зывает, что теплоемкость адиабатного процесса равна нулю.

Поскольку при адиабатном процессе 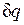= 0, энтропия рабочего тела не изме­няется (ds =0 и s =const). Следователь­но, на Т, s-диаграмме адиабатный про­цесс изображается вертикалью.

Политропный процесс и его обобща­ющее значение. Любой произвольный процесс можно описать в р,v -координатах (по крайней мере на небольшом участке) уравнением

,

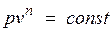подбирая соответствующее значение п. Процесс, описываемый таким уравнением, называется политропным. Показатель политропы n может прини­мать любое численное значение в преде­лах от 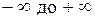, но для данного процесса он является величиной посто­янной.

Из уравнения Клапейрона нетрудно получить выраже­ния, устанавливающие связь между р, v и Т в любых двух точках на политропе, аналогично тому, как это было сделано для адиабаты:

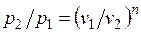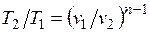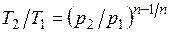; ; . (5.1)

Работа расширения газа в политропном процессе имеет вид .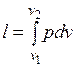

Так как для политропы в соответст­вии с (5.1)

,

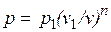то

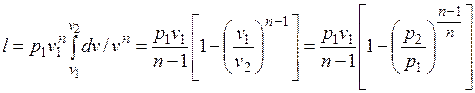(5.2)

Уравнение (5.1) можно преобразо­вать к виду:

Количество подведенной (или отве­денной) в процессе теплоты можно опре­делить с помощью уравнения первого закона термодинамики:.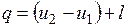

Поскольку 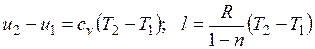, то

,

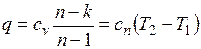где

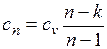
представляет собой теплоемкость иде­ального газа в политропном процессе. При постоянных c_v, k и п теплоемкость с n = const, поэтому политропный процесс иногда определяют как процесс с посто­янной теплоемкостью.

Изменение энтропии

.

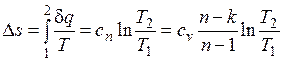Политропный процесс имеет обобща­ющее значение, ибо охватывает всю со­вокупность основных термодинамических процессов. Ниже приведены характери­стики термодинамических процессов.

Процесс	п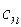
Изохорный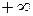
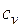
Изобарный	0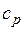
Изотермический	1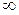
Адиабатный	k	0

На рисунке показано взаимное распо­ложение на р, V- и Т, s-диаграммах политропных процессов с разными значения­ми показателя политропы. Все процессы начинаются в одной точке («в центре»).

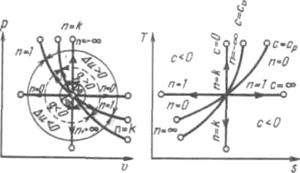
Рисунок 5.5 - Изображение основных термоди­намических процессов идеального газа в р, v- и Т, s-координатах

Изохора (п= ± 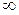) делит поле диаг­раммы на две области: процессы, нахо­дящиеся правее изохоры, характеризу­ются положительной работой, так как сопровождаются расширением рабочего тела; для процессов, расположенных ле­вее изохоры, характерна отрицательная работа.

Процессы, расположенные правее и выше адиабаты, идут с подводом теп­лоты к рабочему телу; процессы, лежа­щие левее и ниже адиабаты, протекают с отводом теплоты.

Для процессов, расположенных над изотермой (= 1), характерно увеличе­ние внутренней энергии газа; процессы, расположенные под изотермой, сопро­вождаются уменьшением внутренней энергии.

Процессы, расположенные между адиабатой и изотермой, имеют отрица­тельную теплоемкость, так как 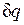и du (а следовательно, и dT), имеют в этой области противоположные знаки. В таких процессах 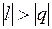, поэтому на производство работы при расширении тратится не только подводимая теплота, но и часть внутренней энергии рабочего тела.

Дата добавления: 2014-10-15