Скорость. Закон движения дается векторным уравнением

Закон движения дается векторным уравнением

. (1)

При координатном способе положение точки А определяется координатами x, y, z, а закон движения задается тремя уравнениями:

(2)

при этом , (3)

где – единичные по модулю и взаимно перпендикулярные векторы-орты системы координат.

Рис. 2

Y

Непрерывная линия, которую описывает точка при своем движении, называется траекторией. На рисунке 2 показана траектория точки. В зависимости от формы траектории различают прямолинейное движение и криволинейное движение (частный случай – движение по окружности).

Рис. 3

Путь – это длина траектории, пройденная точкой. За малый промежуток времени точка пройдет путь .

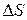Перемещение точки за промежуток времени – вектор , соединяющий положении точки в моменты t и t + . Из рис. 2 видно, что вектор перемещения

. (4)

Мгновенная скорость материальной точки определяется соотношением

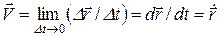, (5)

т.е. мгновенная скорость есть производная радиуса-вектора по времени. Она направлена по касательной к траектории движущейся точки.

В физике принято производные по времени обозначать не штрихом, а (×) над буквой.

Из рис. 2 видно, что при , поэтому модуль скорости

(6)

Можно описать движение через параметры траектории. Для этого некоторую точку на траектории примем за начальную, тогда любая другая точка характеризуется расстоянием S(t) от нее. Радиус вектор становится сложной функцией вида , поэтому из (5) следует:

,

где

– единичный вектор, касательный к траектории; – модуль скорости.

В СИ скорость измеряется в метрах в секунду (м/с).

С учетом формулы (3) из (5) получаем

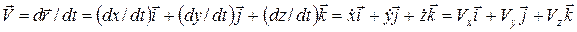, (7)

где

(8)

– компоненты скорости, они равны производным соответствующих координат по времени.

На рис. 2, 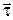обозначает единичный касательный вектор, он совпадает с направлением скорости , поэтому

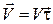. (9)

Дата добавления: 2014-10-15