
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Графіки алгебраїчних функцій
|
|
|
|
Лінійна функція. Функція вигляду 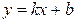 називається лінійною функцією. Графіком функції є пряма лінія, яку можна побудувати за двома точками. Наприклад, якщо
називається лінійною функцією. Графіком функції є пряма лінія, яку можна побудувати за двома точками. Наприклад, якщо 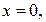 то
то 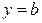 , отже,
, отже, 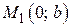 – точка перетину з віссю
– точка перетину з віссю 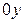 ; якщо
; якщо  , то
, то 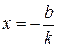 , маємо точку
, маємо точку 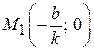 – точку перетину з віссю
– точку перетину з віссю 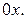
Множник  називається кутовим коефіцієнтом. Його геометричний зміст –
називається кутовим коефіцієнтом. Його геометричний зміст –  , де
, де 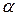 – кут нахилу прямої до додатного напрямку осі
– кут нахилу прямої до додатного напрямку осі 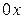
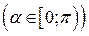 (рис. 4.10).
(рис. 4.10).

Рис. 4.10 Рис. 4.11
Приклад 4.6. Побудувати прямі  і
і 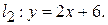 Знайти точку перетину прямих і кут нахилу прямої
Знайти точку перетину прямих і кут нахилу прямої 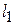 до осі
до осі 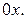
Розв’язання. 1) На 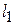 : якщо
: якщо 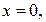 то
то 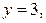 отже,
отже, 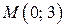 – точка перетину з віссю
– точка перетину з віссю 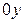 ; якщо
; якщо 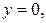 то
то 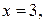 отже,
отже,  – точка перетину з віссю
– точка перетину з віссю 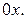 Таким чином, якщо відмітити точки
Таким чином, якщо відмітити точки 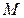 і
і 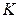 і провести через них пряму, то одержимо графік заданої функції
і провести через них пряму, то одержимо графік заданої функції 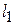 . Аналогічно на
. Аналогічно на  маємо
маємо 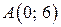 і
і  – точки перетину відповідно з осями
– точки перетину відповідно з осями 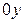 і
і 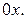 Отже, з’єднуючи точки
Отже, з’єднуючи точки 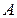 і
і 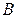 , одержимо пряму
, одержимо пряму  (рис. 4.10). 2) Щоб знайти точку перетину двох графіків, треба прирівняти обидві функції:
(рис. 4.10). 2) Щоб знайти точку перетину двох графіків, треба прирівняти обидві функції:  Розв’язком рівняння є
Розв’язком рівняння є  Підставимо
Підставимо  у будь-яке з рівнянь заданих прямих і одержимо ординату точки перетину
у будь-яке з рівнянь заданих прямих і одержимо ординату точки перетину 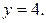 Отже,
Отже,  – шукана точка. 3) Оскільки
– шукана точка. 3) Оскільки 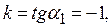 то
то 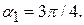
Пряма і обернена пропорційність. Найпростіший вигляд має рівняння прямої, яка проходить через початок координат:  . Таке співвідношення між змінними
. Таке співвідношення між змінними 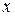 і
і 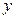 називається прямою пропорційністю, а число
називається прямою пропорційністю, а число  - коефіцієнтом пропорційності
- коефіцієнтом пропорційності
(рис. 4.11, 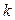 =2).
=2).
Співвідношення  називається оберне ною пропорційністю. Графіком функції є гіпербола. Зазвичай гіперболу будують за точками. Оскільки функція
називається оберне ною пропорційністю. Графіком функції є гіпербола. Зазвичай гіперболу будують за точками. Оскільки функція  є непарною, то спочатку будують одну гілку (для
є непарною, то спочатку будують одну гілку (для 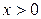 ), а другу будують симетрично початку координат. Прямі
), а другу будують симетрично початку координат. Прямі 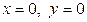 є асимптотами графіка (див. рис. 4.11,
є асимптотами графіка (див. рис. 4.11, 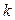 =2).
=2).
Приклад 4.7. Побудувати графік функції 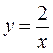 .
.
Розв’язання. Обчислимо кілька значень функції Таблиця 4.2

| 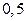
| 
| 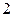
| 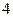
|

| 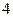
| 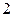
| 
| 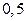
|
та запишемо їх для зручності у табл. 4.2. З
урахуванням симетрії та наявності асимптот будуємо
за точками задану криву (див.рис. 4.11).
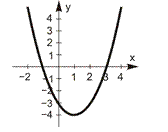
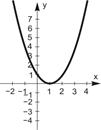
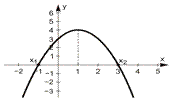
Квадратична функція. Функція вигляду 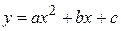 називається квадратичною функцією. Її графіком є парабола. Залежно від коефіцієнта
називається квадратичною функцією. Її графіком є парабола. Залежно від коефіцієнта 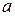 та дискримінанта
та дискримінанта  графік цієї функції може мати вигляд, наведений у табл. 4.3.
графік цієї функції може мати вигляд, наведений у табл. 4.3.
Таблиця 4.3
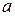 
| 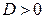
| 
| 
|

| 
|  
| 
|
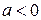
| 
| 
| 
|
| Абсциси вершин | 
 , , 
| 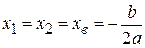
| 
|
Степенева функція. Функція вигляду 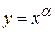 , де
, де  (довільна стала) – показник степеня, називається степеневою функцією від незалежної змінної
(довільна стала) – показник степеня, називається степеневою функцією від незалежної змінної 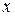 . На рис. 4.12 наведено графіки степеневих функцій при деяких додатних значеннях
. На рис. 4.12 наведено графіки степеневих функцій при деяких додатних значеннях 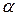 , на рис. 4.11 – для від’ємних.
, на рис. 4.11 – для від’ємних.
Аналізуючи графіки, які наведено на рис. 4.11 і 4.12, можна зазначити таке:
1) функції  ,
, 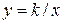 ,
, 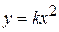 є частковими випадками степеневої функції;
є частковими випадками степеневої функції;
2) коли  , всі графіки проходять через точки (0;0) і (1;1);
, всі графіки проходять через точки (0;0) і (1;1);
3) якщо  , то більшому значенню
, то більшому значенню 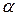 відповідає більше значення
відповідає більше значення 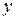 ;
;

Рис. 4.12
4) коли 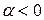 , то
, то 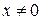 і лінії
і лінії  і
і  є асимптотами графіка функції;
є асимптотами графіка функції;
5) якщо 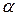 – парне, то графік розташовано у І та ІІ чвертях, а якщо непарне – у І та ІІІ чвертях.
– парне, то графік розташовано у І та ІІ чвертях, а якщо непарне – у І та ІІІ чвертях.
4.3. Графіки тригонометричних функцій
Основними тригонометричними функціями є функції  ,
, 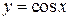 ,
, 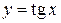 ,
,  . Графіки цих функцій наведено на рис. 4.13 – 4.16.
. Графіки цих функцій наведено на рис. 4.13 – 4.16.

Рис. 4.13

Рис. 4.14


Рис. 4.15 Рис. 4.16
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 676; Нарушение авторских прав?; Мы поможем в написании вашей работы!