Броуновское движение

Броуновским называют непрерывное, хаотическое, равновероятное для всех направлений движение мелких частиц, взвешенных в жидкости или газах, за счет воздействия молекул дисперсионной среды.

Аэрозольную частицу диаметром 100 нм окружают примерно 10⁵газовых молекул, частота колебаний которых (применительно к двухатомным молекулам) составляет 10¹⁴с^-1. Следовательно, одна аэрозольная частица за счет газовых молекул может испытать 10¹⁹ударов за 1 с. Если бы сила ударов, которые получает частица со всех сторон, была одинакова, то частица «топталась» бы на месте.

Мельчайшие частицы незначительной массы испытывают неодинаковые удары со стороны молекул дисперсионной среды; результирующая сила F, которая заставляет частицы двигаться, показана на рис. 9.1 жирной стрелкой. Направление и импульс этой силы непрерывно меняются, поэтому частицы совершают хаотическое движение.

Молекулы дисперсионной среды таким же образом действуют на частицы средне- и грубодисперсных систем. В связи со значительным размером частиц этих систем число ударов молекул резко увеличивается. По законам статистики подобное обстоятельство означает, что импульс действия сил со стороны молекул среды взаимно компенсируется, а значительная масса и инерция относительно крупных частиц способствует тому, что воздействие молекул остается без последствий. Поэтому броуновское движение наиболее интенсивно проявляется в отношении высокодисперсных систем.

Направление результирующей силы F (см. рис. 9.1), вызванной ударами молекул, и движение самих молекул все время изменяются. Определить эти изменения и связать их с молекулярно-кинетическими свойствами среды удалось в 1907 г. независимо друг от друга А. Эйнштейну и М. Смолуховскому.

Рис. 9.1. Воздействие молекул дисперсионной среды на частицу 1 дисперсной фазы.

Рис. 9.2. Сдвиг частиц.

В основу их расчетов был взят не истинный путь частиц дисперсной фазы, а сдвиг частиц (рис. 9.2). Если путь частицы определяется ломаной линией, то сдвиг х характеризует изменение координат частицы за определенный отрезок времени. Средний сдвиг будет определять среднеквадратическое смещение частицы, которое определяется по уравнению

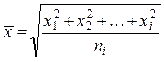, (9.2)

где х₁, х₂, x_i — сдвиг частиц за определенное время.

Теория броуновского движения исходит из представления о взаимодействии случайной силы f(τ), которая характеризует удары молекул, силы F_τ, зависящей от времени, и силы трения при движении частиц дисперсной фазы в дисперсионной среде со скоростью n. Уравнение случайного броуновского движения (уравнение Ланжевена) имеет следующий вид:

m(dν/dt) + ην = F_τ+ f(τ), (9.2, а)

где m — масса частицы; η — коэффициент вязкости дисперсионной среды.

Для больших промежутков времени (τ >> m/η) инерцией частиц, т.е. членом m(dν/dτ), можно пренебречь. После интегрирования уравнения (9.2, а) при условии, что среднее произведение импульсов случайной силы равно нулю, находят среднее значение флуктуации (средний сдвиг):

(9.3)

где τ — время; r — радиус частиц дисперсной фазы; N_A— число Авогадро.

В формуле (9.3) отражены параметры дисперсной фазы и дисперсионной среды: величина RT/N_Aхарактеризует молекулярно-кинетические свойства дисперсионной среды, а η — ее вязкость; радиус частиц r — это параметр, относящийся к дисперсной фазе, а время t определяет взаимодействие дисперсионной среды с дисперсной фазой. Формула (9.3) подтверждена экспериментально.

Кроме поступательного возможно вращательное броуновское движение, характерное для двухмерных частиц и частиц неправильной формы (нитей, волокон, хлопьев и др.).

Средний сдвиг частиц различного размера за одну секунду в воздушной среде характеризуется значениями:

Радиус частиц, мкм 10^-3 0,1 10

Максимальные значения
среднего сдвига, мкм 1,28 ∙ 10³ 0,168 0,0123

Средний сдвиг для частиц высокодисперсных систем размером 10^–3— 10^–1мкм (или 1—100 нм) может достигать нескольких миллиметров.

Броуновское движение наиболее ярко выражено у высокодисперсных систем, а его интенсивность зависит от дисперсности (см. рис. 1.2). Для среднедисперсных систем средний сдвиг составляет единицы или доли микрометров. Если размер частиц превышает 10 мкм, то броуновским движением можно пренебречь. Это обстоятельство является одним из факторов, ограничивающим верхний размер среднедисперсных систем значением 10 мкм.

Дата добавления: 2014-10-15