Методика расчета величины погрешности.

Распределение симметрично относительно максимума.

2. При многократных испытаниях среднее значение стремится к некой постоянной величине.

3. Частость появления погрешностей, равных по абсолютной величине, но противоположных по знаку одинаково.

4. Согласно нормальному закону вероятность появления очень больших отклонений небольшая, но реальная. Применение доверительного интервала к нормальному распределению всегда ограничивает площадь под кривой распределения значением <1, то и вероятность P<1. Последнее обстоятельство показывает, что какой бы большой доверительный интервал при нормальном законе мы ни взяли, всегда произойдет событие, значение которого не попадет в доверительный интервал. Соотношение между доверительным интервалом и вероятностью распределения. Обозначается доверительной вероятностью Pдов, которая всегда <1 и зависит от интервала. Для нормального закона доверительная вероятность связывает интервал через коэффициент Стьюдента. Доверительная вероятность называется коэффициентом надежности измерения. В технике при нормальном законе коэффициент надежности всегда <1.

Если доверительный интервал D=2d, то P=0,96; D=d, то P=0,6.

Величина коэффициента U принимается за коэффициент Стьюдента. Для нормального закона принимается отношение надежности измерения (доверительной вероятности) и доверительного интервала через среднее квадратное отклонение и коэффициент Стьюдента. Как правило, реальные результаты лишь стремятся к тому или иному закону, поэтому доверительный интервал оценивается приблизительно.

Используют нормальный закон как одно из средств достижения результата, т.е. инструмент. Нормальный закон применяют, если число опытов, число случайных переменных большое, случай же выполнения этих требований, по перемене (помехи) коррелированы (связаны) между собой.Используют для описания закон Релея.

Релеевский закон используют при анализе взаимосвязанных характеристик электрических сигналов. Альтернативой нормальному закону в электрических измерениях считается равномерный закон.

Этот подход применяют при анализе результатов измерений, параметры не известный закон. Число погрешностей невелико. Особенность закона в том, что его границы четко определены DXmax» Ö `3 *d Pдов = 1.

Поскольку с уменьшением доверительной вероятности пропорционально снижается интервал, равномерный закон позволяет просто проводить обработку результатов. Если несколько физических величин, имеющих равномерный закон распределения, объединяются в устройстве, результат принимают по треугольному закону распределения.

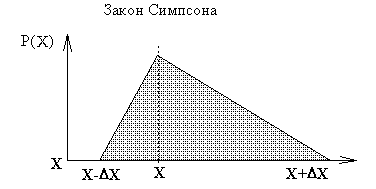
В общем случае треугольник может быть неравносторонним. Площадь треугольника конечна, интервалы фиксируются, поэтому также для симметричного закона DXm =Ö`6 *d при P=1.

Треугольное распределение - некий промежуточный шаг от равномерного к нормальному закону. Если 2-3 величины, имеющие равномерный закон распределения, взаимодействуют, результат близок к треугольному закону.

Применение тех или иных законов для описания входящих переменных, результатов измерений, помогает использовать априорные методики анализа точности измерительных систем. Любая измерительная система имеет ряд функциональных блоков, каждый из которых свои погрешности. Перед началом анализа необходимо определить законы распределения случайных входящих переменных. Рекомендуют в случае неизвестных законов входящих переменных принимать их равномерными.

Задача: анализ точности доверительного интервала измерительных систем. Задание - по номерам из учебного журнала группы.

Дата добавления: 2014-10-15