Оценка надежности программ на ранних стадиях проектирования

Оценка надежности ПО по аналогии с невосстанавливаемыми техническими системами

Оценка надежности ПО по наработке (модель Шумана). Для прогнозирования надежности ПО в этой модели используются данные о числе ошибок, устраненных в процессе компоновки программ в систему ПО и отладки программ. По этим данным вычисляются параметры модели надежности, которая может быть использована для прогнозирования показателя надежности в процессе использования ПО.

Модель основана на следующих допущениях:

- при последовательных прогонах программы наборы входных данных являются случайными и выбираются в соответствии с законом распределения, соответствующим реальным условиям функционирования;

- в начальный момент компоновки программ в систему ПО в них имеется Е₀ ошибок; в ходе корректировок новые ошибки не вносятся;

- общее число I машинных команд в программах постоянно, т.е. I=const;

- интенсивность отказов программы 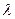пропорциональна числу ошибок, оставшихся в ней после отладки в течение времени , т.е.

(2.24)

где отношение числа ошибок, устраненных в течение времени отладки , к общему числу команд на машинном языке.

Таким образом, в модели различаются два значения времени: время отладки (обычно измеряется месяцами) и время работы программы 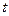- суммарная наработка программы (часы и доли часа). Время отладки включает затраты времени на выявление ошибок с помощью тестов, контрольные проверки и т. п. Время исправного функционирования при этом не учитывается.

Таким образом, значение интенсивности отказов 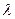считается постоянным в течение всего времени функционирования (0, t). Значение 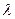изменяется лишь при обнаружении и исправлении ошибок (при этом время 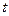вновь отсчитывается от нуля).

В силу принятых допущений для фиксированного вероятность отсутствия ошибок программ в течение наработки времени (0,t):

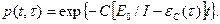(2.25)

Средняя наработка программы до отказа

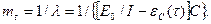(2.26)

Для практического использования формулы (2.26) и (2.25) необходимо оценить и по экспериментальным данным. Для этого можно использовать метод моментов или метод максимального правдоподобия.

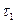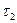Применяя метод моментов и рассматривая два периода отладки программ и при 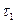<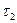, получаем

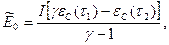
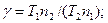
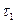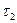где - продолжительность работы системы, соответствующие и ; и 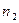- число ошибок в ПО, обнаруженных соответственно в периодах 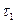и .

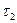Оценка надежности программ по числу прогонов (модель Нельсона). В такой модели за показатель надежности программы принимается вероятность безотказного выполнения n прогонов программы.

Вероятность того, что j – й прогон закончится отказом,

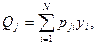(2.27)

где 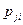- вероятность выбора i -ого набора входных данных при j – м прогоне некоторой последовательности прогонов; - «динамическая переменная», принимающая значение 0, если прогон программы при i – м наборе входных данных оказывается успешным, и значение 1, если этот прогон заканчивается отказом; N – число возможных наборов входных данных.

На практике надежность программы может быть оценена путем прогона программы на n наборах входных данных и вычисления значения оценки

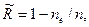
где - число наборов входных данных, при которых произошли отказы.

Для получения вначале находят «функциональный разрез» программы, т. е. множество вероятностей 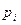того, что будет сделан выбор i –ого варианта входных данных. Для этого разбивают все пространство входных переменных на подпространства и находят вероятности того, что выбранный набор входных данных будет принадлежать конкретному подпространству. Это можно сделать, оценивая вероятности появления различных входов в реальных условиях функционирования, для которых оценивается надежность программы.

Далее формируют случайную выборку из n наборов входных данных, распределенных в соответствии с 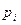(например, с помощью датчика случайных чисел), и проводят n прогонов программы, находят и вычисляют .

Чтобы установить связь между моделями по наработке и по прогонам, запишем

(2.28)

или

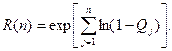(2.29)

Описанные выше модели надежности программ требуют оценки ряда параметров по статистическим данным, получаемым при тестировании, отладке программ или на этапе передачи программ в эксплуатацию [12]. На ранних этапах проектирования программ отсутствует возможность проведения экспериментов, могут быть использованы статистические данные об отказах аналогичных программ, созданных ранее той же группой программистов. Рядом исследователей выявлена стабильность относительной частоты ошибок в различных типовых конструкциях алгоритмических языков высокого уровня. Рассмотрим модель надежности программы, основанную на этом явлении и учитывающую структуру программы и распределение исходных данных.

В этой модели предполагается, что:

а) исходные данные выбираются случайно в соответствии имеющимся распределением их вероятностей;

б) ошибки в элементах программы независимы;

в) программа образована из элементов немногих s классов с одинаковыми вероятностями p_l правильного однократного исполнения элементов класса l.

При этих допущениях условная вероятность p_i правильного однократного пути исполнения программы при условии исполнения пути i:

, (2.30)

где m_li – количество элементов l – ого класса в i - ом пути. (Путь – последовательность элементов программы, не содержащая ответвлений и используемая при выполнении программы с определенными исходными данными.)

Вероятность правильного однократного исполнения всей программы

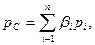(2.31)

где - вероятность выбора i -ого пути (зависит от сочетания значений исходных данных).

Если программа в процессе эксплуатации не корректируется, т. е. проявившиеся ошибки не устраняются, вероятности p_i неизменны. При корректировании программ вероятность правильного однократного исполнения элемента l - го класса в период между (j-1) – й и j - й ошибками

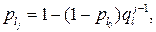(2.32)

где 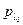- вероятность правильного однократного исполнения элемента l - го класса до начала эксплуатации или отладки программы; q_l – параметр эффективности корректировки (показывает, во сколько раз изменяется вероятность появления ошибки в элементе l – ого класса после ее устранения).

При одинаковых q_l=q вероятность правильного однократного исполнения всей программы между (j-1) и j – м отказами

(2.33)

где p_со - вероятность правильного однократного исполнения программы до начала ее эксплуатации или отладки.

Если программа не корректируется после обнаружения в ней ошибок, q=1. Если корректировки неудачны, например, из-за плохого знания программы, q>1. При 0<q<1 корректировки повышают надежность программы.

Дата добавления: 2014-10-15