Расчет числа невосстанавливаемых запасных частей с периодическим пополнением по вероятности достаточности

Рассмотрим задачу определе­ния числа невосстанавливаемых запасных частей при схеме пополнения запасом, несколько упрощенной по сравнению с рис. 6.3, а - имеется только одно место хранения запасных частей — склад на эксплуатационном предпри­ятии (т. е. задача распределения запасных частей между рабочими местами внутри предприятия не рассматривается). Предположим, что запас пополня­ют через постоянное время t=t₅-t₂=t₇-t₅=…, причем задержки между мо­ментами составления заявок и поступления заказа отсутствуют (см. рис. 6.3, а). Зафиксируем некоторый вид невосстанавливаемых изделий и по аналогии с рис. 5.2 примем, что число этих изделий равно k. Обозначим m=m₁+m_з1. Расчет запаса сводится к определению такого минимального зна­чения т, при котором имеет место неравенство

Q_д(t)≤P{η(t)≤m}, (6.4)

где η(t) — число требований на замену на интервале (t₂, t₅) длиной t.

Примем следующие допущения:

- запасные части при хранении не отказывают;

- поток отказов, потребовавшихся запасных частей для восстановления, стационарный;

- запасные изделия после замены имеют ту же надежность, что и основные.

Рассмотрим сначала соотношения, применяемые в том случае, когда за­пасные части расходуются только на восстановление после отказов. При произвольном стационарном потоке отказов неравенство (6.4) можно пере­писать в виде

(6.5)

где — вероятность отказа изделий за время t.

Данная ситуация соответствует резервированию без восстановления ненагруженным резервом с дробной кратностью.

В простейшем потоке

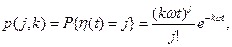(6.6)

где ω - параметр потока отказов одного изделия.

С учетом (6.6) неравенство (6.5) приобретает вид

, (6.7)

Для определения числа запасных изделий можно воспользоваться номо­граммой (рис. 6.5), где по горизонтальной оси от­ложена величина κωt, а по вертикальной — .

Отметим, что если принять начальное значение запаса т₁=0, то получен­ные соотношения могут служить для расчета ЗИП постоянного состава. Составляющая т₁ учитывает переменный состав ЗИП: число запасных час­тей, имеющихся на предприятии в момент составления заявки.

Остановимся на выборе величины . Предположим, что одно устрой­ство включает в себя l типов невосстанавливаемых элементов, а величина задана для совокупности устройства в целом. Определять требования к вероятностям для каждого i -го типа элементов по вероятности можно различными способами (например, с учетом затрат на запас­ные части). Наиболее простой способ при условии независимости отказов элементов заключается в равномерном распределении требований вероят­ности достаточности запаса между составляющими элементами. Тогда

.

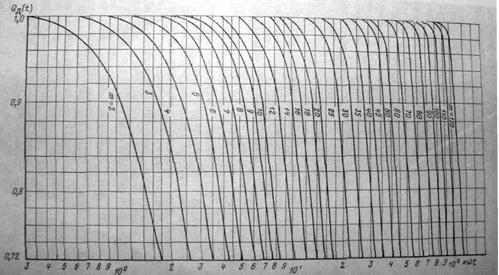
Рис. 6.5Номограмма для определения числа невосстанавливаемых запасных частей при периодическом пополнении

6.2.4 Расчет количества невосстанавливаемых запасных частей по эконо­мическим критериям

Рассмотрим ту же схему организации пополнения запаса, что и в предыдущем варианте при расчете количества невосстанав­ливаемых запасных частей m по вероятности достаточности, приняв те же допущения и обозначения. В отличие от предыдущего варианта число запасных частей будем определять по критерию минимума эксплуатационных расходов G_э на периоде t; пополнения запаса. В простом случае

G_э(m)=c₁m+c₂R, (6.8)

где c₁ — стоимость одного запасного элемента; c₂ — убытки от отсутствия одного запасного элемента; R — случайная величина дефицита запаса.

Убытки c₂ слагаются из стоимости экстренной доставки недостающей за­пасной части (или для некоторых механических деталей — стоимости ее изготовления не на заводе — изготовителе устройства, а на эксплуатационном предприятии) и из ущерба от простоя соответствующего устройства (систе­мы) из-за отсутствия запаса. Величина

, (6.9)

или

. (6.10)

Перейдем к математическому ожиданию случайных величин G_э и R:

.(6.11)

Задача сведена к отысканию т, при котором функция имеет мини­мум.

Для этого нужно найти значение m, при котором разность

меняет знак.

Это значение m легко найти графически. Для этого достаточно построить зависимость 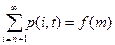(рис. 6.6, а).

Пересечение этой зависимости с горизонтальной прямой с₁/с₂ дает иско­мое значение т. При простейшем потоке отказов значение оптимального за­паса можно находить по графикам, приведенным на рис. 6.6, б.

Задача определения оптимального количества запасных элементов не од­ного, как рассмотрено выше, а r типов с учетом их стоимости при той же стратегии пополнения запаса и при наличии ограничений часто формулиру­ется в одном из двух следующих вариантов:

1. Задано ограничение с₀ суммарной стоимости ЗИП:

, (6.11)

где l —число типов элементов; с_i —стоимость одного элемента i-го типа;

т - число запасных элементов i-го типа.

Требуется определить величины (т_1, т₂,..., т_l,), при которых показатель достаточности запаса, например вероятность достаточности , будет максима­лен.

2. Задано ограничение по значению показателя достаточности, например

, (6.12)

где А - некоторая величина.

Требуется определить (т_1, т₂,..., т_l,) так, чтобы достигался минимум за­трат

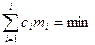. (6.13)

Решение этих задач может проводиться методами линейного програм­мирования.

Рис. 6.6 График для определения числа запасных элементов по

экономическому критерию

6.2.5 Расчет количества восстанавливаемых запасных частей по вероятно­сти достаточности

Рассмотрим определение количества восстанавливаемых запасных частей при схеме, несколько упрощенной по сравнению с рис. 6.4 (имеется только один склад). Ремонт проводится в мастерской эксплуатаци­онного предприятия или в сервисном предприятии. Предположим, что на предприятии функционируют k однотипных восстанавливаемых изделий, а искомое число запасных изделий обозначим т.

Примем следующие допущения:

- запасные изделия при хранении не отка­зывают;

- поток отказов изделий простейший с параметром ω;

- ремонт полно­стью восстанавливает свойства изделия;

- восстановление неограниченное (любое отказавшее изделие сразу же поступает на ремонт, т. е. число ремонт­ников достаточно для одновременного восстановления всех отказавших из­делий);

- длительность пребывания изделия на восстановлении описывается экспоненциальным распределением с параметром μ.

Рассмотренная ситуация при определении вероятности достаточности соответствует резервированию ненагруженным резервом с неограниченным восстановлением. Вероятность безотказной работы системы, состоящей из k основных и m резервных элементов,

(6.14)

Рис. 6.7 Номограмма для определения числа восстанавливаемых систем запасных частей

Величина запаса находится как такое наименьшее значение m, при котором соблюдается неравенство

. (6.15)

Определить величину можно по номограмме (рис. 6.7), где по горизонтальной оси отложена величина , а по вертикальной - . Номограмма построена для t=7500 ч.

Дата добавления: 2014-10-15