Уравнение непрерывности

Рассмотрим полупроводник, в котором в результате внешнего воздействия возникают неравновесные свободные носители заряда. Изменение с течением времени концентрации неравновесных носителей в любом физически бесконечно малом объёме полупроводника будет определяться не только генерацией и рекомбинацией свободных носителей заряда, но и движением заряженных частиц. Дифференциальное уравнение, которому подчиняется в этих условиях концентрация свободных носителей заряда, называют уравнением непрерывности.

Вывод уравнения непрерывности проведём в одномерном приближении, считая уровень возбуждения малым. Получим уравнение непрерывности для электронов. Рассмотрим физически бесконечно малый контрольный объём dΩ=dSdx, расположенный от x до x+dx (рис. 1.5.7). Изменение числа электронов в выделенном контрольном объёме может происходить в результате:

• генерации и рекомбинации носителей;
• втекания и вытекания носителей.

Полное изменение числа электронов dN в объёме dΩ за время dt в результате действия всех факторов равно

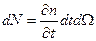. (1)

Изменение числа электронов dN₁ за счёт процессов генерации и рекомбинации равно

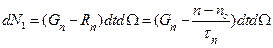. (2)

Здесь мы учли, что уровень возбуждения предполагается малым, и потому использовали линейный закон рекомбинации (см. §1.4).

Изменение в контрольном объёме числа электронов dN₂ за счёт процессов втекания и вытекания носителей вдоль оси OХ равно

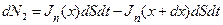. (3)

Рис.1.5.7.К выводу одномерного уравнения непрерывности для электронов.

Здесь J_n (шт/см²с) -проекция вектора плотности потока свободных электронов на ось OХ. Поскольку плоскости, через которые происходит втекание и вытекание носителей, находятся на малом расстоянии dx, то можно представить значение J_n(x+dx) в виде разложения функции J_n(х) в ряд Тейлора в окрестности точки с координатой x и ограничиться линейным приближением

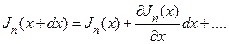. (4)

Подставив (4) в (3), находим

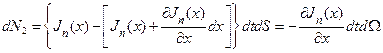. (5)

Поскольку

dN = dN₁+dN₂, (6)

то с учётом (1), (2) и (5) после сокращения на общий множитель dtdΩ получаем

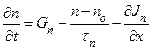. (1.5.23)

Это и есть уравнение непрерывности для электронов в случае, когда их концентрация зависит только от одной пространственной координаты x, а закон рекомбинации можно считать линейным. Для трёхмерного случая при линейном законе рекомбинации уравнение непрерывности для электронов примет вид

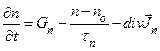. (1.5.24)

Уравнение непрерывности для дырок при линейном законе рекомбинации имеет аналогичный вид. Для одномерного случая

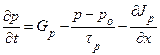. (1.5.25)

Для случая, когда концентрация и вектор плотности потока дырок зависят от времени и трёх пространственных переменных, имеем

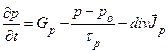. (1.5.26)

Между плотностью потока заряженных частиц и плотностью создаваемого ими полного тока существует линейная связь. Для дырок в проекции на ось ОХ она имеет вид

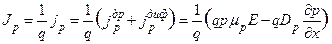
или

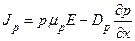. (1.5.27)

Подставляя (1.5.27) в (1.5.25) и полагая коэффициент диффузии дырок не зависящим от координаты, получим ещё одну форму записи одномерного уравнения непрерывности для дырок

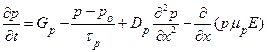. (1.5.28)

Если в рассматриваемой области полупроводника напряженность электрического поля мала настолько, что дрейфовый механизм движения дырок можно не учитывать, то одномерное уравнение непрерывности для дырок принимает вид

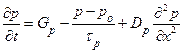. (1.5.29)

Аналогичные соотношения для электронов будут иметь вид

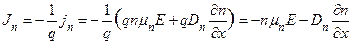, (1.5.30)

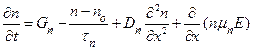. (1.5.31)

Если последним слагаемым правой части (1.5.31) можно пренебречь, то одномерное уравнение непрерывности для электронов примет вид

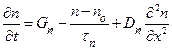. (1.5.32)

Дата добавления: 2014-10-15