
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры
|
|
|
|
Найти  :
:
а) 


б) 

в) 

г) 

д) 

Задание 10
Дифференциальное уравнение (ДУ) первого порядка имеет вид 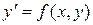 или
или 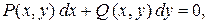 где
где  у – искомая функция от переменной х,
у – искомая функция от переменной х, 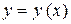 .
.
Процесс решения ДУ называется его интегрированием.
а) ДУ с разделяющимися переменными имеет вид
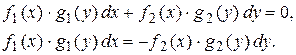 (1)
(1)
Пусть 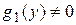 и
и  Разделим обе части уравнения (1) на произведение
Разделим обе части уравнения (1) на произведение 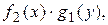 получим ДУ с разделенными переменными
получим ДУ с разделенными переменными
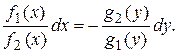 (2)
(2)
Равенство (2) означает, что дифференциалы двух функций равны,, значит сами функции отличаются лишь на постоянное слагаемое. Интегрируя равенство (2), получим общее решение или общий интеграл ДУ (1)

Пример: Проинтегрировать ДУ

Разделим переменные и проинтегрируем обе части равенства
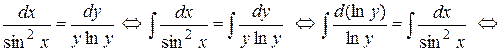
 - общий интеграл исходного ДУ, где
- общий интеграл исходного ДУ, где 
Задание 11
а) Найти частное решение ДУ  удовлетворяющее условию
удовлетворяющее условию 
Разделяем переменные


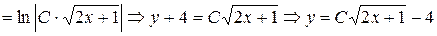 - общее решение данного уравнения.
- общее решение данного уравнения.
Определим постоянную С так, чтобы выполнялось начальное условие 
 Получаем частное решение данного уравнения в виде
Получаем частное решение данного уравнения в виде 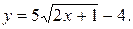
Линейное ДУ 1 порядка относительно функции 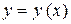 и ее производной
и ее производной  имеет вид
имеет вид
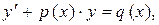 (3)
(3)
где  и
и  - заданные непрерывные функции.
- заданные непрерывные функции.
Заменой  решение ДУ (3) сводится к решению двух ДУ с разделяющимися переменными.
решение ДУ (3) сводится к решению двух ДУ с разделяющимися переменными.
б)Найти частное решение ДУ  (4)
(4)
удовлетворяющее начальному условию 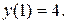
Находим общее решение уравнения (4) с помощью замены 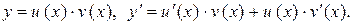 Подставляем эту замену в уравнение (4)
Подставляем эту замену в уравнение (4)
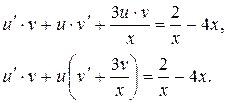
Функции  и
и 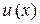 определяем из условий
определяем из условий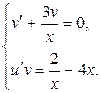
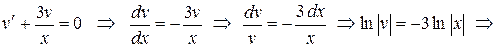



Общее решение ДУ (4) имеет вид 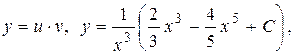

Определим С из начального условия 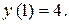

Искомое частное решение имеет вид 
Задание 12
Исследовать числовые ряды на сходимость.
| а) |  ; ;
| б) |  ; ;
| в) | 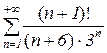 ; ;
|
Решение:
а) Мы имеем ряд 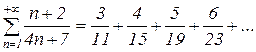 . Его члены положительны и убывают. Найдем к чему стремится его n -ый член при стремлении n к бесконечности:
. Его члены положительны и убывают. Найдем к чему стремится его n -ый член при стремлении n к бесконечности:
 .
.
Значит, необходимое условие сходимости ряда не выполняется и ряд расходится.
б) Мы имеем ряд  . Его члены положительны и убывают. Найдем к чему стремится его n -ый член при стремлении n к бесконечности:
. Его члены положительны и убывают. Найдем к чему стремится его n -ый член при стремлении n к бесконечности:
 .
.
Значит, необходимое условие сходимости ряда выполняется и ряд может как сходиться, так и расходиться.
Исследуем данный ряд по предельному признаку сравнения, согласно которому два ряда сходятся или расходятся одновременно, если  . Так как в числителе максимальная степень n равна 1, а в знаменателе – 2, то сравнивать будем с гармоническим рядом
. Так как в числителе максимальная степень n равна 1, а в знаменателе – 2, то сравнивать будем с гармоническим рядом  (
(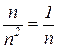 ). Найдем предел отношения общих членов исходного и гармонического рядов при стремлении n к бесконечности:
). Найдем предел отношения общих членов исходного и гармонического рядов при стремлении n к бесконечности:
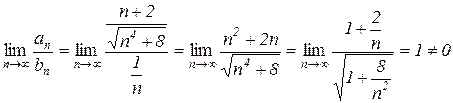 .
.
Таким образом, по предельному признаку сравнения, исходный ряд и гармонический сходятся или расходятся одновременно. Так как гармонический ряд расходится, то расходится и исходный ряд.
в) Мы имеем ряд 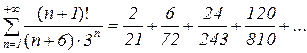 . Его члены положительны и убывают. Так как в числителе общего члена ряда присутствует факториал, а в знаменателе степень, то при проверке стремления этого члена при стремлении n к бесконечности получим довольно сложный предел:
. Его члены положительны и убывают. Так как в числителе общего члена ряда присутствует факториал, а в знаменателе степень, то при проверке стремления этого члена при стремлении n к бесконечности получим довольно сложный предел:
 ,
,
то вычислять его не будем.
Исследуем данный ряд на сходимость по предельному признаку Д’Аламбера: если  , то при
, то при 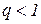 данный ряд сходится, при
данный ряд сходится, при  – расходится, при
– расходится, при  – требуется исследовать по другим признакам.
– требуется исследовать по другим признакам.
Поскольку 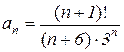 ,
,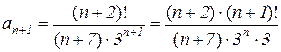 , то
, то
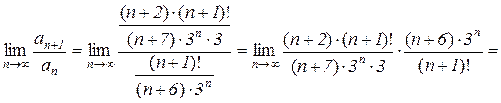
 .
.
Следовательно, данный ряд расходится.
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 265; Нарушение авторских прав?; Мы поможем в написании вашей работы!