Тема 3. 5 динамические модели систем

До сих пор основное внимание было уделено понятию системы, ее составу и устройству. Были построены модели, которые являются как бы "фотографиями" системы, отображают ее в некоторый момент времени. В этом смысле рассмотренные варианты моделей "черного ящика", состава, структуры и структурной схемы системы могут быть названы статическими моделями, что подчеркивает их неподвижный, как бы застывший характер.

Следующий шаг в исследовании систем состоит в том, чтобы понять и описать, как система "работает", что происходит с ней самой и с окружающей средой в ходе реализации поставленной цели. Очевидно, и подход к описанию, и степень подробности описания происходящих процессов могут быть различными. Однако общим при этом является то, что разрабатываемые модели должны отражать поведение систем, описывать происходящие с течением времени изменения, последовательность каких-то этапов, операций, действий, причинно-следственные связи.

Системы, в которых происходят какие бы то ни было изменения со временем, будем называть динамическими, а модели, отображающих эти изменения, — динамическими моделями систем.

Для разных объектов и систем разработано большое количество динамических моделей, описывающих процессы с различной степенью детальности: от самого общего понятия динамики, движения вообще, формальных математических моделей конкретных процессов типа уравнений движения в механике или волновых уравнений в теории поля Развитие моделей происходит примерно в той последовательности, как это было изложено: от "черного ящика" к "белому". Однако этот путь конкретизации моделей непрост и нелегок и для многих систем еще не закончен из-за недостаточности имеющихся знаний.

Уже на этапе "черного ящика" различают два типа динамики системы: ее функционирование и развитие. Под функционированием подразумевают процессы, которые происходят в системе (и окружающей её среде), стабильно реализующей фиксированную цель (функционируют, например, часы, городской транспорт, кинотеатр, канцелярия, радиоприемник, станок, школа, и т.д.). Развитием называют то, что происходит с системой при изменении ее целей. Характерной чертой развития является тот факт, что существующая структура перестает соответствовать новой цели, и для обеспечения новой функции приходится изменять структуру, а иногда и состав системы, перестраивать всю систему.

Не следует считать, что система всегда находится либо в фазе развития, либо в состоянии функционирования. При реконструкции одного цеха остальные функционируют, завод в целом развивается. Даже при коренной перестройке системы какие-то элементы и даже подсистемы старой структуры могут продолжать функционировать в новой по-прежнему. Возможны и такие системы, для функционирования которых какие-то ее подсистемы должны быть постоянно в развитии.

Следующий шаг в построении динамических моделей состоит в том, чтобы конкретнее отобразить происходящие изменения. Это означает, что следует различать части, этапы происходящего процесса, рассматривать их взаимосвязи. Иными словами, типы динамических моделей такие же, как и статических, только элементы этих моделей имеют временной характер. Например, динамический вариант "черного ящика" — указание начального ("вход") и конечного ("выход") состояний системы. Модели состава соответствует перечень этапов в некоторой упорядоченной последовательности действий. Например, доказано, что любой алгоритм можно построить, используя всего три оператора: "выполнять последовательно", "если... то..." и "выполнять, пока не удовлетворится условие". Эти операторы можно рассматривать как модель минимального состава алгоритма, хотя не обязательно составлять алгоритм только из этих операторов. Динамический вариант "белого ящика" - это подробное описание происходящего или планируемого процесса. Например, на производстве широко используют так называемые сетевые графики — графы, имеющие сетевую структуру; их вершинами служат выполняемые производственные операции, а ребра указывают, какие операции не могут начаться, пока не окончатся предыдущие. Здесь же некоторым образом (например, с помощью задания длин или весов ребер) изображается длительность выполнения операций, что и позволяет находить на графе "критические" пути, т.е. последовательности операций, от которых главным образом зависит ритмичность всей работы.

Те же типы моделей прослеживаются и при более глубокой формализации динамических моделей. При математическом моделировании некоторого процесса его конкретная реализация описывается в виде соответствия между элементами множества Х возможных "значений х и элементов упорядоченного множества Т "моментов времени" t, т.е. в виде отображения Т -> Х: x (t)  ХT, t  T. С помощью этих понятий можно строить математические модели систем.

Рисунок 3.7. Динамическая модель "черного ящика": задание процессов на входах и выходах системы.

Рассматривая выход y (t) системы (это может быть вектор) как её реакцию на управляемые u (t) и неуправляемые v (t) входы x (t) = { u (t), v (t) } (рис. 3.7), можно модель "черного ящика" выразить как совокупность двух процессов: XT= {x(t)} и УT= {y(t)}, t  Т. Если даже считать y (t) результатом некоторого преобразования Ф процесса x (t), т.е. y(t) = Ф(х(t)), то модель "черного ящика" предполагает, что это преобразование неизвестно. В том же случае, когда мы имеем дело с "белым ящиком", соответствие между входом и выходом можно описать тем или иным способом. Какой именно способ — зависит от того, что нам известно, и в какой форме можно использовать эти знания.

Например, иногда бывает известно, что система мгновенно преобразует вход в выход, т.е. что y (t) является функцией только x(t) в тот же момент времени. Остается задать или найти эту функцию. На практике чаще всего известна лишь безынерционность системы и требуется, наблюдая входы и выходы, восстановить неизвестную функцию у = Ф(х). По существу, это задача о переходе от модели "черного ящика" к модели "белого ящика" по наблюдениям входов и выходов при наличии информации о безынерционности системы. Даже в такой достаточно простой постановке задача имеет совсем не простые варианты, которые зависят от того, что известно о функции Ф (в параметризованном случае Ф принадлежит семейству функций, известных с точностью до параметров; в не параметризованном — вид функции Ф неизвестен), и от наличия или отсутствия некоторых общих сведений о ее свойствах (непрерывности, гладкости, монотонности, симметричности и т.п.). Дополнительные варианты (и дополнительные трудности) возникают, если входы и выходы наблюдаются с помехами или искажениями. При этом разные предположения о природе этих помех приводят к принципиально отличающимся решениям задачи (например, в случае, когда распределены помехи известно точно, известно с точностью до числовых параметров или неизвестно совсем).

Однако класс систем, которые можно считать безынерционными, весьма узок. Необходимо строить математические модели систем, выход которых определяется не только значением входа в данный момент времени, но и теми значениями, которые были на входе в предыдущие моменты. Более того, в самой системе с течением времени как под влиянием входных воздействий, так и независимо от них могут происходить изменения, что также следует отразить в модели.

В наиболее общей модели это достигается введением понятия состояния системы как некоторой (внутренней) характеристики системы, значение которой в настоящий момент времени определяет текущее значение выходной величины. Состояние можно рассматривать как своего рода хранилище информации, необходимой для предсказания влияния настоящего на будущее Обозначим это состояние через z (t). Все сказанное выше означает существование такого отображения : Z* T-> Y, что

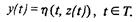
Явная зависимость  от t введена для учета возможности изменения зависимости выхода от состояния с течением времени. Это отображение называется отображением выхода.

Для завершения построения модели нужно описать связь между входом и состоянием, т.е. ввести параметрическое семейство отображений t:Z*X(.)->Z, заданных для всех значений параметров t  Т,   T и   t. Это означает принятие аксиомы о том, что состояние в любой момент t >  однозначно определяется состоянием zв момент  и отрезком реализации входа х (.) от  до t:

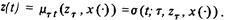
Такое отображение называют переходным отображением.

Итак, математическая модель системы, соответствующая уровню "белого ящика", — это задание множеств входов, состояний и выходов, и связей между ними:

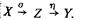
Конкретизируя множества X, Z и У и отображения  и , можно перейти к моделям различных систем. Так, говорят о дискретных и непрерывных по времени системах в зависимости от того, дискретно или непрерывно множество Т. Далее, если множества X, Z и Y дискретной по времени системы имеют конечное число элементов, то такую систему называют конечным автоматом. Это довольно просто класс систем в том смысле, что для исследования конечных автоматов необходимы лишь методы логики и алгебры; в то же время это широкий и практически важный класс, так как в него входят все дискретные (цифровые) измерительные, управляющие и вычислительные устройства, в том числе и ЭВМ. Если X, Z и У — линейные пространства, а  и , - линейные операторы, то и система называется линейной. Если к линейной системе дополнительно предъявить требования, состоящие в том, чтобы пространства имели топологическую структуру, а  и  были бы непрерывны в этой топологи, то мы приходим к гладким системам. Это класс систем имеет большое значение, так как оказалось, что для гладких систем переходное отображение  является общим решением дифференциального уравнения

(dz/dt) =f (t, z, x),

а для дискретных систем - общим решением уравнения

z (tk+1) =f (tk, z, х) =  (tk+1,; tk, z, х (.)),

где х (.) — траектория для моментов времени

t <= tk

Интенсивно исследовались стационарные системы, т.е. такие системы, свойства которых со временем не изменяются. Стационарность означает независимость от t функции  и инвариантность функции  к сдвигу во времени:

 (t. z (t)) = (z (t)),  (t; t0, z, x (.)) =  (t+ ; t0+ , z,!x (.)),

где!x (.) есть х (.), сдвинутое на время .

Конкретизация моделей динамических систем на этом, конечно, не заканчивается; приведенные модели, скорее всего, являются просто примерами, которые можно рассматривать отдельно. Но на одном свойстве реальных динамических систем следует остановиться. Речь идет о подчиненности реальных систем принципу причинности. Согласно этому принципу, отклик системы на некоторое воздействие не может начаться раньше самого воздействия. Это условие, очевидное для реальных систем, совсем не автоматически выполняется в рамках их математических моделей. При этом модель, в которой нарушается принцип причинности, не обязательно является "плохой", бесполезной. Примером служит модель фильтра с конечной полосой пропускания: отклик такой системы на короткий импульс имеет вид sin (w0t/(w0t)), т.е. начинается в минус бесконечности. Несмотря на явное нарушение принципа причинности, такую модель широко используют в радиотехнике. Однако, как только возникает вопрос о практической реализации такого фильтра, становится ясно, что она невозможна в точном смысле, хотя допустимы различные приближения. В связи с этим одна из проблем теории динамических систем состоит в выяснении условий физической реализуемости теоретических моделей, т.е. конкретных ограничений, которые приходится накладывать на модель при соблюдении принципа причинности.

Подведем итог:

Модели, отображающие процессы, происходящие в системе с течением времени, называются динамическими моделями. Динамические модели включают те же типы, что и статические, но с явным выделением, подчеркиванием роли времени.

Всякая реальная динамическая система подчинена принципу причинности: отклик не может появиться раньше стимула. Условия, при которых модель отражает этот принцип, называются условиями физической реализуемости модели; нахождение этих условий часто является нетривиальной задачей.

Раздел IV. РАЗЛИЧНЫЕ КЛАССИФИКАЦИИ СИСТЕМ

Начиная сравнивать и различать системы, считать одни из них одинаковыми, другие — различными, мы тем самым вводим и осуществляем их классификацию.

Важно понять, что классификация — это только модель реальности (Можно было бы даже сказать — первичная, простейшая модель, если бы не тот факт, что вследствие многоуровневой, кратной, вложенной классификации полученная модель может и не отвечать понятию "простейший"). Поэтому классификацию не следует абсолютизировать - реальность всегда сложнее любой модели.

Так, можно считать, что в систему "рыболовецкое холзяйство" не входит промысловая акватория, в "леспромхоз" не входят лесные делянки, а "всаднка" мыслим без лошади.

Естественно, напрашивается введение еще одного класса смешанных систем, объединяющих искусственные и естественные подсистемы. Теперь такая классификация уже может претендовать на полноту. Вообще, полнота классификации является предметом особого внимания при ее построении. Иногда есть уверенность в полно вводимой классификации, иногда нет (и тогда имеет смысл ввод класс "все остальное"), а иногда наша уверенность оказывается самонадеянным незнанием

"Очевидное" разделение всех людей на мужчин и женщин "не срабатывает" не только для гермафродитов, и на генетическом уровне: в начале 80-х годов в международном спорте был введен генетический тест в некоторых женских олимпийских видах. Это еще одна иллюстрация модельности, условности всякой классификации.

Тема 4.1 КЛАССИФИКАЦИЯ СИСТЕМ ПО ИХ ПРОИСХОЖДЕНИЮ

Часто оказывается необходимым провести разграничение внутри одного класса, не отказываясь тем не менее от общности в его рамках. Так появляются подклассы, что приводит к. многоуровневой, иерархической классификации. При необходимости такая классификация может быть продолжена без изменения ее верхних уровней. Например, двухуровневая классификация систем по происхождению изображена на рис. 1. Если полнота классификации первого уровня логически ясна, то второй уровень на полноту не претендует. Неполнота на этом уровне связана, например, с еще незавершенным развитием систем искусственного интеллекта. В качестве примеров подклассов смешанных систем можно привести эргономические системы, биотехнические и организационные системы. Классификация естественных систем ясна из рис. 4.1; ее неполнота очевидна. Например, не решен окончательно вопрос о том, куда следует отнести вирусы: к живым или неживым системам. Или, скажем, идея В.И. Вернадского о ноосфере шире рамок экологических и социальных систем.

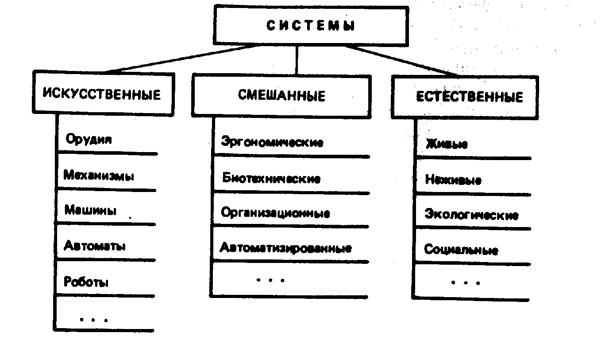
Рисунок 4.1. Классификация систем по их происхождению

Как было отмечено ранее, модель имеет целевой характер. Не является исключением и классификация: новые цели, учет новых различий между системами порождают и новые классификации. Чтобы как-то упорядочить подходы к классификации систем, воспользуемся общей схемой функционирования системы (рис. 4.2), выделив отдельно систему S подлежащую управлению U, и управляющую систему, которая это управление вырабатывает. Подчеркнем, что для выработки управления U требуется предсказание его последствий, т.е. нужна модель всей ситуации с помощью этой модели управляющая система и определяет, какое управление подать на управляемый вход системы. Это иллюстрирует рис. 4.2, где схема изображена еще раз внутри управляющего блока.

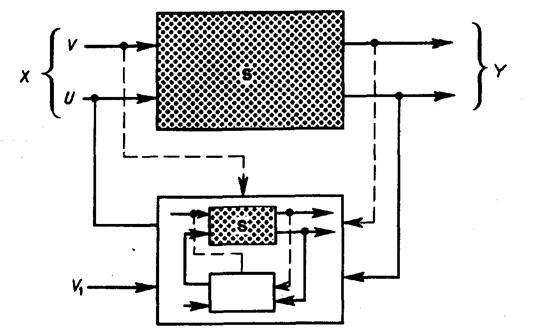
Рисунок 4.2. Схема функционирования управляемой системы

И методы нахождения управления U, и способы его осуществления и сам результат управления в немалой степени определяются тем, что известно о системе и что учитывается при выработке управления, т.е. тем, какова модель управляемой системы, и тем, в какой степени эта модель соответствует реальной системе. Рассматривая разные аспекты этого соответствия, можно строить разные классификации систем. Например, представляют интерес следующие классификации: по описанию входных и выходных процессов; по описанию оператора S системы; по типу управления; по обеспеченности управления ресурсами.

Дата добавления: 2014-10-15