
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Розв’язання. 1. Розкладемо квадратний тричлен
|
|
|
|
Розв’язання.
1. Розкладемо квадратний тричлен 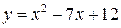 . Для цього розв’яжемо квадратне рівняння
. Для цього розв’яжемо квадратне рівняння  :
: 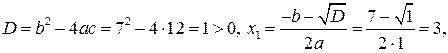
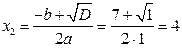 . Нерівність
. Нерівність  запишемо у вигляді
запишемо у вигляді 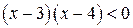 і застосуємо метод інтервалів.
і застосуємо метод інтервалів.
2. 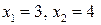 – нулі функції (рис. 5.2).
– нулі функції (рис. 5.2).
3. Визначаємо знак нерівності на кожному інтервалі:
 :нехай
:нехай  , тоді
, тоді  ;
;
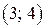 :нехай
:нехай 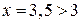 , тоді
, тоді 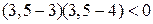 ;
;
 :нехай
:нехай  , тоді
, тоді  .
.
Виберемо проміжки зі знаком нерівності "-". Маємо  .
.
Приклад5.10. Розв’язати нерівність .
.
1. Нулі заданої функції –  . Вони розбивають числовий інтервал на 4 проміжки (рис. 5.3). Оскільки нерівність не строга, то точки
. Вони розбивають числовий інтервал на 4 проміжки (рис. 5.3). Оскільки нерівність не строга, то точки  і
і  включаємо до розв’язку.
включаємо до розв’язку.

Рис. 5.3
2. Визначаємо знак нерівності на інтервалі 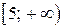 : візьмемо
: візьмемо 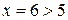 , тоді
, тоді  .
.
3. Подвійних точок нерівність не має. Тому скористаємося умовою зміни знака: 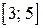 – "+";
– "+";  – "-";
– "-"; 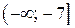 – "+". Маємо
– "+". Маємо 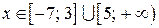 .
.
Приклад 5.11. Розв’язати нерівність
Розв’язання. ОДЗ: 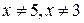 . Відмітимо на числовій прямій точки
. Відмітимо на числовій прямій точки  ,
,  (нулі чисельника) і
(нулі чисельника) і  ,
,  (нулі знаменника). Нерівність записано в стандартному вигляді, тому праворуч від точки
(нулі знаменника). Нерівність записано в стандартному вигляді, тому праворуч від точки  функція додатна. Усі показники степеня непарні, тому при переході через них знак лівої частини нерівності буде змінюватися (рис. 5.4). Маємо
функція додатна. Усі показники степеня непарні, тому при переході через них знак лівої частини нерівності буде змінюватися (рис. 5.4). Маємо 

Рис. 5. 4
Завдання для самостійної роботи
5.6. Розв’язати нерівності:
а) ; b)
; b)  ; c)
; c)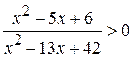 ;
;
d)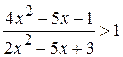 ; e)
; e) ; f)
; f) ;
;
g) ; h)
; h)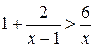 ;
;
i)  ; j)
; j)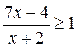 ; k)
; k) ; l)
; l)  .
.
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 276; Нарушение авторских прав?; Мы поможем в написании вашей работы!