Упругом основании

Исходные данные к заданию № 10

Функции прогибов

Вариант	Функция направления х	Функция направления у

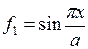
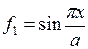
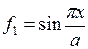
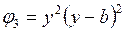
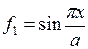
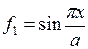
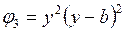
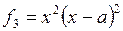
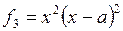
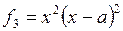
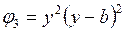
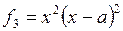
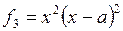
Таблица 13

Вариант	а, см	b, см	h, см	Е, МПа	n	q, кН/м^2	F, кН	xF, см	уF, см
				1,0×10^5	0,30
				1,2×10^5	0,31
				1,4×10^5	0,30
				1,6×10^5	0,30
				1,8×10^5	0,30
				2,0×10^5	0,31
				2,1×10^5	0,30
				2,2×10^5	0,31
				2,1×10^5	0,31
				1,8×10^5	0,30
				1,2×10^5	0,31
				1,4×10^5	0,30
				1,6×10^5	0,31
				1,8×10^5	0,31
				2,0×10^5	0,30

Задание № 11. Расчет балки на сплошном

Для балки, лежащей на сплошном упругом основании требуется определить внутренние усилия и перемещения, используя соответствующие уравнения метода начальных параметров.

Работа выполняется в два этапа. На первом этапе необходимо записать уравнения деформаций и внутренних усилий для каждого участка балки.

Напряженно-деформированное состояние балки, лежащей на сплошном упругом основании, зависит от жесткостных характеристик балки и упругого основания. Этими характеристиками являются:

EJ_z – изгибная жесткость балки;

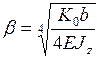– коэффициент жесткости,

где Е – модуль упругости материала балки, кН/м²; J_z – момент инерции поперечного сечения балки, м⁴; K ₀ – коэффициент податливости упругого основания, зависящий от свойств грунта, кН/м³; b – ширина поперечного сечения балки, м.

При расчете методом начальных параметров начало координат выбирается в крайней левой точке балки. Поскольку реакция упругого основания изменяется непрерывно по длине балки, то для построения криволинейных эпюр деформаций и внутренних усилий необходимо определить их значения для нескольких точек по длине.

Начальные параметры зависят от граничных условий. В табл. 14 представлены уравнения в зависимости от действующих внешних нагрузок. В этих уравнениях y ₀, j ₀, M ₀, Q ₀ – начальные параметры, из которых два всегда равны нулю (табл. 15). Неизвестные начальные параметры определяются из условий закрепления правого края балки.

В уравнения y, j, M, Q (табл. 14) входят функции Y ₁(x), Y ₂(x), Y ₃(x), Y ₄(x), названные функциями Крылова-Коши, значения которых определяются в зависимости от аргумента bx, где x – координаты точек балки в принятой системе координат:

Y ₁(x) = ch bx × cos bx;

Y ₂(x) = 0,5(ch bx × sin bx + sh bx × cos bx);

Y ₃(x) = 0,5sh bx × sin bx;

Y ₄(x) = 0,25(ch bx × sin bx – sh bx × cos bx).

В зависимости от характера действующих нагрузок и от условий закреплений левого конца балки для каждого участка необходимо записать уравнение по форме, представленной в табл. 14.

Поскольку при составлении уравнений для различных сечений каждый раз рассматривается часть балки слева от сечения, то в уравнение для каждого последующего сечения входят все слагаемые уравнения в предыдущих сечениях. Поэтому запись уравнений для любого сечения может быть представлена в виде табл. 16.

Дата добавления: 2014-10-15