
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Методи побудови початкового опорного плану
|
|
|
|
Як і в симплексному методі розв’язування задач лінійного програмування, при розв’язуванні транспортної задачі потрібно мати початковий опорний план.
Розглянемо методи знаходження цього плану:
1. Діагональний метод (північно-західного кута).
Побудову початкового опорного плану за методом північно-західного кута починають із заповнення лівої верхньої клітинки таблиці A 1 B 1 (х 11), в яку записують менше з двох чисел а 1 та b 1. Далі переходять до наступної клітинки в рядку або стовпчику і заповнюють її і т.д., закінчуючи останньою правою клітинкою таблиці AmBn (хmn).
Розглянемо алгоритм побудови початкового опорного плану транспортної задачі методом північно-західного кута:
1. Перевірка транспортної задачі на закритість. Якщо вона відкрита, то приводимо її до задачі закритого типу введенням або фіктивного постачальника або фіктивного споживача.
2. Першою заповнюємо верхню ліву клітинку. Заповнення клітинки AiBj таблиці здійснюємо за такими правилами:
а) якщо аi < bj, тобто запаси менші від потреб, то в цю клітинку записуємо весь об’єм запасу вантажу аi, перераховуємо потреби споживача Bj, постачальника Ai вилучаємо з розгляду (наприклад, поставивши у всіх клітинках рядочка, крім заповненої, прочерки) і переходимо до заповнення наступної клітинки Ai+1Bj;
б) якщо аi > bj, тобто запаси більші від потреб, то в цю клітинку записуємо весь об’єм потреб вантажу bj, перераховуємо запаси постачальника Ai, вилучаємо з розгляду споживача Bj (ставимо у всіх клітинках стовпчика, крім заповненої, прочерки) і переходимо до заповнення наступної клітинки AiBj+ 1;
в) якщо аi = bj, тобто запаси рівні потребам, то в цю клітинку записуємо весь об’єм потреб чи запасів, вилучаємо з розгляду постачальника Ai і споживача Bj (ставимо в усіх клітинках стовпчика і рядка, крім заповненої, прочерки) і переходимо до заповнення наступної клітинки Ai+1Bj+1.
3. Серед незаповнених клітинок (без обсягу вантажу і прочерків) знову вибираємо верхню ліву клітинку таблиці і заповнюємо її за правилами, поданими в п. 2. Так продовжуємо до тих пір, доки не заповнимо всі клітинки таблиці.
4. З одержаної таблиці виписуємо початковий опорний план транспортної задачі та обчислюємо значення цільової функції при цьому плані.
2. Метод найменшої вартості.
Правила знаходження початкового опорного плану транспортної задачі методом найменшої вартості відрізняються від правил знаходження такого плану діагональним методом тільки послідовністю вибору клітинки, яку потрібно заповнювати. Згідно з методом найменшої вартості першою вибирається клітинка з найменшою вартістю перевезення одиниці вантажу від постачальника до споживача. Якщо таких клітинок декілька, то вибираємо ту, для якої кількість вантажу, що можна перевезти, найбільша.
Після побудови початкового опорного плану кожним з методів у таблиці ма’ бути заповнено (т+п-1) клітинок, тому що ранг матриці системи обмежень транспортної задачі рівний r=m+n-l, де т- кількість постачальників, п - кількість споживачів. Заповнені клітинки називаються базисними, а незаповнені - вільними. Якщо кількість базисних клітинок рівна (т+п-1), то такий план називається невиродженим. Якщо кількість заповнених клітинок менша (т+п-1), то план називається виродженим. Тоді необхідно заповнити відповідну кількість порожніх (небазисних) клітинок, записуючи в них «нульове перевезення», і ці клітинки вважати базисними. Коли ж кількість заповнених клітинок перевищує (т+п-1), то початковий опорний план побудовано неправильно і він не є опорним.
5.3. Метод потенціалів
5.3.1. Критерій оптимальності опорного плану за методом потенціалів
Ми вже знаємо методи знаходження початкових опорних планів транспортної задачі, але чи ці опорні плани є оптимальними, тобто такими, що дають найменшу загальну вартість перевезення всього вантажу від постачальників до споживачів, ми не знаємо. Опорний план перевіряють на оптимальність за допомогою потенціалів. Відповідно до кожного постачальника Aі ставимо потенціал uі aкожному споживачу  .
.
Критерій оптимальності опорного плану транспортної задачі
якщо для деякого опорного плану (хіj) транспортної задачі існують такі числа-потенціали uі та vj що для базисних клітинок виконуються рівності  , а для небазисних клітинок виконуються нерівність
, а для небазисних клітинок виконуються нерівність  для всіх
для всіх  , то такий опорний план є оптимальним.
, то такий опорний план є оптимальним.
Потенціали опорного плану визначаються із рівнянь системи  , які записують для всіх заповнених клітинок таблиці транспортної задачі. За допомогою розрахованих потенціалів перевіряють умову оптимальності
, які записують для всіх заповнених клітинок таблиці транспортної задачі. За допомогою розрахованих потенціалів перевіряють умову оптимальності  - для незаповнених клітинок таблиці. Якщо хоча б для однієї небазисної клітинки ця умова не виконується, тобто
- для незаповнених клітинок таблиці. Якщо хоча б для однієї небазисної клітинки ця умова не виконується, тобто 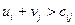 , то поточний план не є оптимальним і потрібно перейти до нового опорного плану.
, то поточний план не є оптимальним і потрібно перейти до нового опорного плану.
5.3.1. Цикли перерахунку транспортної задачі
Перехід від одного опорного плану до іншого виконують заповненням небазисної клітинки, для якої порушена умова оптимальності. Якщо окреслених клітинок кілька, то для заповнення вибирають таку, що має найбільше порушення, тобто max { 
 . Для вибраної порожньої клітинки будують цикл перерахунку.
. Для вибраної порожньої клітинки будують цикл перерахунку.
Циклом у транспортній задачі називають замкнену ламану лінію, сторони якої проходять уздовж рядків і стовпчиків таблиці, і одна з вершин якої знаходиться в небазисній клітинці, для якої порушена умова оптимальності, а всі інші вершини - базисні клітинки.
Перерозподіл продукції в межах циклу здійснюють за такими правилами:
а) кожній вершині циклу приписують певний знак, причому незаповненій клітинці знак «+», а всім іншим по черзі знаки «-» та «+»;
б) у порожню клітинку заносять найменше з чисел, що стоять у клітинках зі знаком «-». Одночасно це число додають до відповідних чисел, що стоять у клітинках зі знаком «+» і віднімають від чисел, що розміщені у клітинках зі знаком «-».
Отже, клітинка, що була вільною, стала заповненою, а відповідна клітинка, де знаходилося найменше число (у вершині з «-») стала незаповненою. В результаті такого перерозподілу продукції ми отримаємо новий опорний план транспортної задачі, який знову перевіряємо на оптимальність. Якщо розв’язок оптимальний, то обчислюємо мінімальне значення цільової функції (мінімальну вартість перевезення всього вантажу), а якщо неоптимальний, то знову будуємо цикл перерахунку і з допомогою зсуву по циклу переходимо до нового опорного плану. Процес повторюють до тих пір, доки не отримаємо оптимального розв’язку транспортної задачі.
Значення базисних клітинок, які не брали участі в циклі перерахунку, в новій таблиці залишаються без змін.
Якщо на деякому кроці потреби співпадають із запасами, то в потребах ставимо дійсний нуль, а в запасах – фіктивний (нуль з крапкою – О). Тоді одразу будується повна система рівнянь для знаходження значень потенціалів.
У задачах з виродженим планом часто зсув стосовно циклу треба робити на 0. Тоді при переході до наступної таблиці значення базисних клітинок, що брали участь в циклі перерахунку, не змінилося. Тільки цей «базисний нуль» переводять у небазисну клітинку, для якої по суті робили цикл перерахунку, а клітинка, в якій знаходився цей 0, стає вільною.
5.4 Практичне застосування транспортної задачі
5.4.2. Модель оптимального розподілу фінансових ресурсів банку
Обсяг фінансових ресурсів банку визначається наявністю певної кількості грошових коштів у тій або іншій валюті. При здійсненні кредитних операцій виникають ситуації, коли банк не має можливості задовольнити клієнта в конкретній валюті. Тому як альтернативні варіанти позичальнику пропонуються кредити в іншій валюті в поєднанні з наданням послуг відносно конвертації валюти кредиту у необхідну валюту. Разом з тим процентна ставка для кредиту в певній валюті кожному позичальнику встановлюється індивідуально, виходячи з існуючих відносин між банком і позичальником, ризикованості операції, конкурентної та рейтингової позицій банку тощо.
При проведенні подібних операцій з великою кількістю клієнтів виникають певні труднощі у знаходженні оптимального варіанта серед множини існуючих, який забезпечив би потребу позичальників у кредитах і прибуток банку був би максимальним.
Для розв’язання поставленої проблеми можна побудувати економіко-математичну модель, яка зводиться до задачі транспортного типу, і далі використати математичний інструментарій або програмні продукти математичного програмування.
Припустимо, що банк має п видів вільних ресурсів (грошових коштів у різних видах валют), на які в конкретний час є попит, і планується їх розподілити між m позичальниками (юридичними чи фізичними особами).
Для побудови економіко-математичної моделі задачі введемо такі позначення: i – індекс виду валюти,  ; j – індекс позичальника,
; j – індекс позичальника, 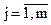 ; bj – обсяг кредиту у гривневому еквіваленті виділеного j -му позичальникові; сij – процентна ставка відносно кредиту для j- го позичальника у валюті і -го виду; аi – обсяг вільних ресурсів банку в і- му виді валюти; xij – невідома величина, яка визначає обсяг кредиту виділеного для j- го позичальника в і -му виді валюти.
; bj – обсяг кредиту у гривневому еквіваленті виділеного j -му позичальникові; сij – процентна ставка відносно кредиту для j- го позичальника у валюті і -го виду; аi – обсяг вільних ресурсів банку в і- му виді валюти; xij – невідома величина, яка визначає обсяг кредиту виділеного для j- го позичальника в і -му виді валюти.
Необхідно знайти оптимальну стратегію розподілу наявних фінансових ресурсів, яка забезпечить максимальний прибуток банку від проведення кредитних операцій.
Враховуючи введені позначення, математична модель оптимального розподілу вільних фінансових ресурсів банку набуде вигляду.
Знайти такий план { xij ≥ 0,  ,
, 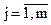 }, який забезпечить
}, який забезпечить
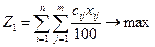
при виконанні умов:
1) з обсягу вільних ресурсів банку
 ,
,  ;
;
2)з обсягу виділених кредитів позичальникам
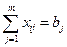 ,
, 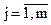 ;
;
2) рівноваги попиту та пропозиції
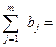
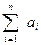
Проте у повсякденній діяльності банку можуть виникнути ситуації, за яких попит перевищує наявні кредитні резерви, тобто має місце

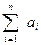
У випадку перевищення попиту над пропозицією стосовно кредитних резервів банк може додатково використати міжбанківський кредит обсягом d грошових одиниць за умови, якщо йому це економічно вигідно. Величина міжбанківського кредиту становитиме:
 -
-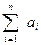 .
.
Далі вводимо додаткові позначення: l - індекс банку, у якому взято кредит, l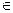 L - множина банків-постачальників; уil - обсяг міжбанківського кредиту взятого у l- мубанку у валюті і- гoвиду; Рil - процентна ставка відносно міжбанківського кредиту для l -го банку у валюті i -го виду; Qil - максимально можливий обсяг міжбанківського кредиту в l -му банку у валюті і- гoвиду.
L - множина банків-постачальників; уil - обсяг міжбанківського кредиту взятого у l- мубанку у валюті і- гoвиду; Рil - процентна ставка відносно міжбанківського кредиту для l -го банку у валюті i -го виду; Qil - максимально можливий обсяг міжбанківського кредиту в l -му банку у валюті і- гoвиду.
Тоді цільова функція матиме вигляд:

при виконанні умов:
1) з обсягу наявних вільних ресурсів банку з врахуванням міжбанківського кредиту
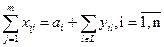 ;
;
2) з обсягу виділених кредитів позичальникам
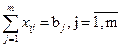 ;
;
3) стосовно розмірів міжбанківських кредитів
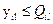 .
.  . l
. l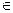 L;
L;
4) стосовно невід’ємності змінних
 ,
,  ,
,  , l
, l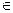 L,
L, 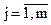 .
.
Побудовані цільові функції Z1 та Z2 відображають інтереси тільки основного банку і не враховують зацікавленості самих позичальників. Тому доцільно окреслену задачу розв’язати як багатокритеріальну і тим самим одержати компромісний план.
У менеджменті банківської діяльності можливі й інші не менш цікаві з практичної сторони проблемні ситуації, які можуть бути представлені як задачі транспортного типу. Як ситуаційні можна навести такі приклади:
- банківський портфель цінних паперів містить декілька пакетів акцій різних фінансових установ і на ринку банківської продукції є декілька покупців, зацікавлених у придбанні цих акцій;
- банківський портфель містить векселі однієї фінансової структури, але з різними термінами погашення та різною дохідністю, з однієї сторони, і потенційні клієнти кредитування векселів - з іншої.
5.4.3. Модель формування штатного розпису фірми
Припустимо, що деяка фірма здійснює процедуру формування штатного розпису. Позначимо: j - індекс посад, 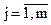 ; i– індекс групи кандидатів на займані посади,
; i– індекс групи кандидатів на займані посади,  . У цей момент часу фірма має п груп різних посад, у кожній із яких є
. У цей момент часу фірма має п груп різних посад, у кожній із яких є  вільних. Претенденти на вакансії проходять тестування, за результатами якого їх ділять на п груп по
вільних. Претенденти на вакансії проходять тестування, за результатами якого їх ділять на п груп по  кандидатів у кожній групі. Для кожного кандидата з і- тої групи необхідні певні витрати
кандидатів у кожній групі. Для кожного кандидата з і- тої групи необхідні певні витрати  на навчання для призначення його на j -ту посаду. Тут можливі випадки, за яких кандидат повністю відповідає посаді, якщо
на навчання для призначення його на j -ту посаду. Тут можливі випадки, за яких кандидат повністю відповідає посаді, якщо 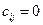 ; кандидат взагалі не може обіймати посаду, якщо
; кандидат взагалі не може обіймати посаду, якщо  =
= 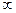 .
.
Ставиться завдання про оптимальний розподіл кандидатів на відповідні посади, за умови мінімальних фінансових витрат на їхнє навчання.
Для знаходження оптимальної стратеги дій припустимо, що число претендентів відповідає числу запропонованих вакансій. У цьому випадку отримуємо транспортну задачу закритого типу. В протилежному випадку маємо справу з транспортною задачею відкритого типу. Тут постачальником виступає група претендентів на вакансії, а в ролі споживача виступають групи вакантних посад.
Витрати на навчання кандидатів  будуть слугувати тарифами перевезень. Невідомими величинами задачі будуть хij - кількість кандидатів і -тої групи, які призначаються на j -ту посаду.
будуть слугувати тарифами перевезень. Невідомими величинами задачі будуть хij - кількість кандидатів і -тої групи, які призначаються на j -ту посаду.
Зурахуванням введених позначень, економіко-математична модель задачі матиме вигляд:
Знайти такий розв’язок  хij > 0,
хij > 0,  ,
, 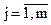 }, який забезпечить
}, який забезпечить
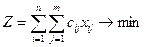
при виконанні умов:
1) всі кандидати на посади повинні бути працевлаштованими
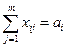 .
. 
2) всі вакантні посади повинні бути заповненими
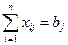 .
. 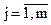
3) рівноваги попиту та пропозиції
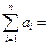
 .
.
ТЕМА 6. ЗАДАЧІ ЦІЛОЧИСЛОВОГО ЛІНІЙНОГО ПРОГРАМУВАННЯ ТА МЕТОДИ ЇХ РОЗВ'ЯЗАННЯ
6.1 Постановка задачі цілочислового лінійного програмування.
6.2 Методи розв'язування задач цілочислового лінійного програмування.
6.3 Прикладні моделі задач цілочислового лінійного програмування.
6.1. Постановка задачі цілочислового лінійного програмування
Існує досить широкий клас задач математичного програмування, в оптимальному розв’язку яких змінні приймають дробові значення, що з економічної точки зору не має змісту, наприклад, коли говориться про випуск певної продукції (комп’ютерів, меблів, станків і т.д.). Тому це призвело до нового класу задач - задач цілочислового програмування. В загальному випадку така задача має вигляд:
Знайти максимум (мінімум) функції
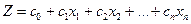 (6.1)
(6.1)
за умов
 (6.2)
(6.2)
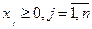
 (6.3)
(6.3)
До задач цього класу можна віднести задачу про використання сировини, транспортну задачу, задачу раціонального розкрою матеріалів, а інший клас задач цілочислового програмування містить задачі оптимізації, в яких змінні набувають лише двох цілих значень - 0або 1 (бульові змінні). Прикладом такої задачі є задача про комівояжера, її зміст полягає в тому, що комівояжеру потрібно відвідати кожне з п міст, починаючи і закінчуючи свій маршрут в одному й тому ж місті і не заїжджаючи двічі в одне місто. Якщо між містами і та j немає прямого маршруту, то вважають, 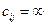 (на практиці беруть достатньо велике число). Крім цього, можливо, що
(на практиці беруть достатньо велике число). Крім цього, можливо, що  . Задача полягає у знаходженні найкоротшого шляху комівояжера. Математична модель задачі має вигляд:
. Задача полягає у знаходженні найкоротшого шляху комівояжера. Математична модель задачі має вигляд:

 (6.4)
(6.4)
де  - відстань між містами і та j;
- відстань між містами і та j;  - бульові змінні:
- бульові змінні:
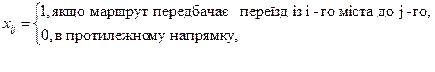
Обмеження, задані першою формулою в системі (6.4), - це умова щодо одноразового в’їзду в кожне місто, а другою формулою - щодо одноразового виїзду з кожного міста.
Розглянемо ще один приклад задачі з бульовими змінними. Інвестиційна компанія може вкласти кошти в декілька підприємств. Ефективність кожного проекту оцінена згідно з тим, що його реалізація можлива за певних умов. Кожному проекту відповідає невідома, яка рівна 1 чи 0 залежно від того, вкладає чи не вкладає інвестиційна компанія кошти в підприємство.
В деяких реальних задачах ставиться умова цілочислових значень не до всіх змінних, а до однієї чи декількох. Такі задачі називають частково цілочисловими.
6.2. Методи розв’язування задач цілочислового лінійного програмування
Для знаходження оптимального розв’язку цілочислових задач використовують спеціальні методи. Найпростішим методом розв’язування цілочислової задачі є знаходження її оптимального розв’язку, як задачі, що має неперервні змінні, з подальшим округленням останніх. Такий підхід часто є виправданим. Проте якщо мова йде про випуск продукції великої вартості (наприклад, турбіни до електростанцій чи агрегату в сушильний цех), то будь-які заокруглення недопустимі.
Для знаходження оптимальних планів цілочислових задач застосовують дві основні групи методів:
- методи відтинання;
- комбінаторні методи.
Основою методів відтинання є ідея поступового «звуження» області допустимих розв’язків задачі. Спочатку розв’язується задача з так званими послабленими умовами, тобто без урахування вимог цілочисельності змінних, а потім вводять в модель додаткові обмеження, які враховують вимогу, щоб значення змінних були цілими. Таким чином многокутник допустимих розв’язків послабленої задачі поступово зменшуємо до тих nip, доки змінні оптимального розв’язку не набудуть цілих значень. Основним методом цієї групи є метод Гоморі.
Комбінаторні методи цілочислової оптимізації базуються на повному переборі всіх допустимих цілочислових розв’язків, тобто вони реалізують процедуру цілеспрямованого перебору, під час якої розглядається лише частина розв’язків (досить невелика), а решта враховується одним із спеціальних методів.
Найпоширенішим в цій групі є метод «віток і меж», який, починаючи з розв’язування послабленої задачі, передбачає розбиття початкової задачі на дві підзадачі виключенням областей, що не мають цілочислових розв’язків, і дослідженням кожної окремої частини многокутника допустимих розв’язків.
Для розв’язування задач з бульовими змінними використовують комбіновані методи, і якщо змінні є бульовими, то методи пошуку оптимального розв’язку значно спрощуються.
Розглянемо детальніше метод Гоморі. Нехай маємо задачу цілочислового програмування (6.1)-(6.3). Для її розв’язування застосовують наступний алгоритм:
1. Використовуючи симплекс-метод, знаходять розв’язок послабленої задачі, тобто задачі без вимог цілочисельності змінних - (6.1)-(6.2). Якщо серед елементів умовно-оптимального плану немає дробових чисел, то цей план є оптимальним планом задачі цілочислового програмування (6.1)-(6.3).
2. Якщо в умовно-оптимальному плані є дробові значення, то вибирається змінна, яка має найбільшу дробову частину. На базі цієї змінної та елементів рядка останньої симплекс-таблиці, що відповідає цій змінній будується додаткове обмеження Гоморі:
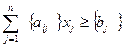 , (6.5)
, (6.5)
де символ { } означає дробову частину числа.
Для визначення дробової частини будь-якого числа необхідно від нього відняти цілу його частину - найбільше ціле число, що не перевищує зазначеного. Цілу частину числа позначають [ ].
3. Додаткове обмеження після зведення його до канонічної форми приєднується до останньої симплекс-таблиці, яка містить умовно-оптимальний розв’язок задачі. Отриману розширену задачу розв’язують, а потім перевіряють її розв’язок на цілочисельність. Якщо він не цілочисловий, то повертаються до пункту 2. Процедуру повторюють до знайдення цілочислового оптимального розв’язку або буде доведено, що задача не має допустимих розв’язків у множині цілих значень. Досвід показує, що процес розв’язування задач великої розмірності методом Гоморі повільно збіжний.
6.3. Прикладні моделі задач цілочислового лінійного програмування (модель формування оптимальної інвестиційної програми при заданому бюджеті)
У окресленій моделі цільовою функцією виступає вартість капіталу інвестиційної програми, причому в ній при заданих обмеженнях (конкретної виробничої програми для окремих інвестиційних об’єктів і за наявності повного обсягу фінансових ресурсів) необхідно сформувати та визначити інвестиційну програму.
Для побудови моделі зробимо такі припущення:
1) представлені на вибір інвестиційні об’єкти рівнозначні;
2) фінансові ресурси неможливо залучити в необмеженій кількості за вказаною відсотковою ставкою;
3) інвестиційна програма визначається тільки на початок планового періоду, а початкові витрати при цьому не перевищують зазначений бюджет;
4) інвестиційні об’єкти реалізуються як єдине ціле.
Для побудови моделі введемо такі позначення: і – індекс інвестиційного об’єкта,  ; Сі - вартість капіталу і- гоінвестиційного об’єкта; Аі0 - затрати на придбання і- гоінвестиційного об’єкта; Q - загальний обсяг бюджетних коштів; хі - бінарна змінна (хі = 0 або 1), значення якої визначає, буде для і -го інвестиційного об’єкта виділене фінансування чи ні.
; Сі - вартість капіталу і- гоінвестиційного об’єкта; Аі0 - затрати на придбання і- гоінвестиційного об’єкта; Q - загальний обсяг бюджетних коштів; хі - бінарна змінна (хі = 0 або 1), значення якої визначає, буде для і -го інвестиційного об’єкта виділене фінансування чи ні.
Враховуючи введені позначення, економіко-математична модель формування оптимальної інвестиційної програми при окресленому бюджеті матиме вигляд.
Знайти такий розв’язок  , який забезпечить сумарну максимальну вартість інвестиційної програми:
, який забезпечить сумарну максимальну вартість інвестиційної програми:
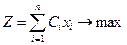 (6.6)
(6.6)
при умовах:
1) з використання наявного обсягу бюджетних коштів
 (6.7)
(6.7)
2) з реалізації інвестиційних об’єктів як єдиного цілого (неподільності інвестиційних об’єктів)
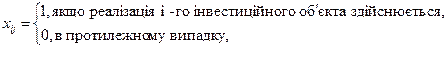
Таким чином, ми отримали задачу лінійного програмування з бульовими змінними. Розв’язок цієї задачі можна знайти з допомогою процедури цілочислового програмування.
ТЕМА 7. НЕЛІНІЙНІ ОПТИМІЗАЦІЙНІ МОДЕЛІ ЕКОНОМІЧНИХ СИСТЕМ
7.1 Постановка задачі нелінійного програмування та її характерні особливості.
7.2 Основні види задач нелінійного програмування. Прикладне використання методу множників Лагранжа.
7.1. Постановка задачі нелінійного програмування та її характерні особливості
До цього часу ми розглядали задачі лінійного програмування, тобто всі невідомі і в цільову функцію, і в обмеження задачі входили лінійно. Проте взаємозв’язки між економічними показниками досить часто носять нелінійний характер і побудована лінійна модель в такому випадку буде неадекватна реальній дійсності. Тому доцільно досліджувати певні економічні пронеси з допомогою нелінійних моделей, математичним інструментом яких є нелінійне програмування.
В загальному випадку задача нелінійного програмування має вигляд:
Z = f(x1,x2,...,xn) max(min), (7.1)
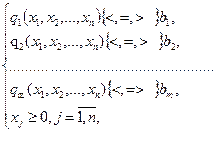 (7.2)
(7.2)
де f(x1,x2,...,xn) та 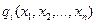 - нелінійні функції.
- нелінійні функції.
Часто задачу нелінійного програмування намагаються привести до лінійного виду. Для лінійних задач завжди можна знайти оптимальний розв’язок універсальним (симплексним) методом. При цьому немає проблеми з доведенням існування такого розв’язку, адже в результаті розв’язання задачі симплексним методом завжди отримуємо один із варіантів відповіді:
1) знайдено оптимальний розв’язок;
2) задача суперечлива, тобто її розв’язку не існує;
3) цільова функція необмежена, отже, розв’язку також немає.
Для задач нелінійного програмування не існує універсального методу розв’язування, тому кожного разу треба доводити існування розв’язку задачі, а також його єдиність. При розв’язуванні нелінійних задач використовують наближені методи, більшість яких дають змогу знаходити локальні оптимуми, а вже знайшовши всі локальні оптимуми, методом порівняння значень цільової функції у кожній з точок локального оптимуму можна знайти глобальний.
7.2. Основні види задач нелінійного програмування
Для розв’язування задач нелінійного програмування не існує універсального методу, а тому доводиться застосовувати багато методів та обчислювальних алгоритмів, які в основному ґрунтуються на теорії диференціального числення, і вибір їх залежить від конкретної постановки задачі та форми економіко-математичної моделі.
Методи нелінійного програмування бувають прямі та непрямі. Прямими методами оптимальні розв’язки шукають у напрямку найшвидшого збільшення (зменшення) цільової функції. Типовими для цієї групи методів є градієнтні. Непрямі методи полягають у зведенні задачі до такої, знаходження оптимального розв’язку якої вдається спростити. Найпоширенішими методами цього класу є методи квадратичного програмування.
Оптимізаційні задачі, на змінні яких накладаються обмеження, розв’язуються методами класичної математики. Оптимізацію з обмеженнями-рівностями виконують методами зведеного градієнта, наприклад, методом множників Лагранжа. У задачах оптимізації з обмеженнями-нерівностями досліджують необхідні та достатні умови існування екстремуму Куна-Таккера.
Розглянемо метод множників Лагранжа на прикладі такої задачі нелінійного програмування:
Z = f(x1,x2,...,xn) max(min), (7.3)
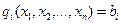 ,
,  (7.4)
(7.4)
де f(x1,x2,...,xn) та 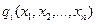 - диференційовані.
- диференційовані.
Ідея методу Лагранжа полягає в заміні окресленої задачі простішою - знаходження екстремуму складнішої функції, але без обмежень. Ця функція називається функцією Лагранжа і записується у вигляді:
 (7.5)
(7.5)
де  - невизначені поки що величини, так звані множники Лагранжа.
- невизначені поки що величини, так звані множники Лагранжа.
Необхідною умовою екстремуму функції багатьох змінних є рівність нулю частинних похідних стосовно всіх змінних функції. Візьмемо ці частинні похідні і прирівняємо їх до нуля:
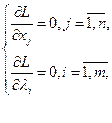
Отримуємо систему (m+n) рівнянь із (т+n) невідомими, розв’язавши яку, знайдемо 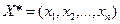 та
та  - стаціонарні точки. Оскільки їх знайдено з необхідної умови екстремуму, то в них можливий максимум або мінімум. Іноді стаціонарна точка є сідловою (точкою перегину графіка функції).
- стаціонарні точки. Оскільки їх знайдено з необхідної умови екстремуму, то в них можливий максимум або мінімум. Іноді стаціонарна точка є сідловою (точкою перегину графіка функції).
Теорема. Нехай в околі критичної точки 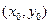 функція
функція  має неперервні частинні похідні до другого порядку включно. Розглянемо вираз
має неперервні частинні похідні до другого порядку включно. Розглянемо вираз
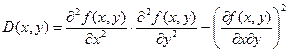
1) Якщо 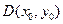 > 0, то в точці
> 0, то в точці 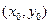 функція
функція  має такі екстремуми:
має такі екстремуми:
а) досягає свого максимального значення, якщо  < 0;
< 0;
б) досягає свого мінімального значення, якщо  > 0;
> 0;
2) Якщо 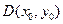 < 0, то в точці
< 0, то в точці 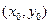 функція
функція  не має екстремумів.
не має екстремумів.
3) Якщо 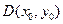 =0, то в точці
=0, то в точці 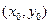 для функції
для функції 
екстремуми можуть існувати чи не існувати.
Розглянемо задачі квадратичного програмування, які є частковим випадком задач опуклого програмування, в яких цільова функція є сумою лінійної та квадратичної форми.
Квадратичною формою відносно змінних х1;х2,...,хи є числова
функція цих змінних вигляду:
Z = сих2 + с22х22 +... + сппх2п + 2с12ххх2 + 2с13х1х3 +... + 2сХпхххп +...+
+ ^n_Xnxn_xxn=fjfjcijxixj 1=17=1 Квадратична форма 2{Х) називається додатно (від’ємно) визначеною, якщо Z(X)>0 (Z(X)<0) для всіх значень змінних Х = (х1,х2,...,хп), крім Х=0.
Квадратична форма Z(X) називається напіввизначеною, якщо Z(X)>0 (Z(X)<0) для всіх значень змінних X = (х1,х2,...,хп), крім
цього існує такии вектор X =(х1,х2,...,хи), не всі координати
котрого рівні нулю і для якого Z(X) = 0.
Квадратична форма Z(X) називається неозначеною, якщо ії значения є додатними для одних значень Х і від’ємними для інших.
Вид квадратично* форми можна визначити через власні значения (характеристичні корені) А = (Л[,Л2,...,Лп) матриці коефіцієнтів С, де
с
;
;
1 и 2 и
V иі и 2
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 2147; Нарушение авторских прав?; Мы поможем в написании вашей работы!