Нормальные формы булевых функций

Пример.

Законы де Моргана

Пример.

Пример.

Докажем закон поглощения (элиминации) аналитически, используя тождества с константами и дистрибутивный закон:

;

.

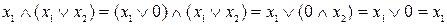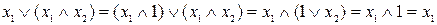Закон инволюции (двойного отрицания)

.

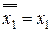Для доказательства закона инволюции (двойного отрицания)используем таблицу истинности (таблица 3.14).

Таблица 3.14 - Закон двойного отрицания

;

.

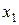
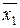
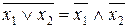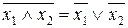Для доказательства закона де Морганаиспользуем таблицу истинности (таблица 3.15).

Таблица 3.15 - Доказательство закона де Моргана

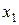
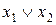
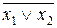
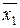
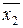
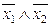
Второй закон де Моргана является двойственным первому и, значит, также является верным.

При практическом применении теории булевых функций часто ставится задача поиска наиболее простой (в определенном смысле) формулы среди всех эквивалентных между собой формул, представляющих рассматриваемую булеву функцию.

На примере булевых функций обсудим важное понятие «нормальной формы», то есть синтаксически однозначного способа записи формулы, реализующей заданную функцию. Данный способ основан на рассмотрении представления логических функций в виде суперпозиций функций 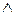(«и»), 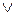(«или»), («не»).

Введем понятия, определяющие способ представления формул в виде дизъюнктивных и конъюнктивных нормальных форм.

Дата добавления: 2014-10-22