Дисперсия суммы и разности переменных

В педагогике и психологии довольно часто требуется определить дисперсию нескольких сложенных значений Х и Υ.

Дисперсия Χ + Υ, где каждая из n сумм равна Χ_i + Υ_i, имеет следующее определение:

. (7.7)

При этом

. (7.8)

Очевидно, что 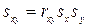. Поэтому замена 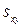на эквивалентное выражение дает

. (7.9)

Уравнения (7.8) и (7.9) связывают дисперсию суммы двух множеств значений с дисперсией каждого множества и их ковариациeй.

Важен особый случай уравнения (7.9), когда X и Y некоррелированы, то есть r_ху = 0. Если это справедливо, то

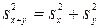. (7.10)

Что же представляет собой выражение, эквивалентное ?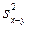

Дисперсия разности между значениями X и Y равна дисперсии X плюс дисперсия Y минус удвоенная ковариация X и Y (или удвоенное произведение r_xy на s_x и s_y). Далее, если X и Y не коррелированы, то

. (7.11)

Рассмотренные результаты полезны не только в дальнейшем процессе изучения статистики, они могут также кое-что прояснить. Например, мы знаем, что

.

Поэтому, если мы разделим это соотношение на 2 s_xs_y, то найдем, что

.

Предположим, что существуют три переменные – X, Y и Z. Чему была бы равна дисперсия сумм, полученных при сложении значений этих трех переменных?

. (7.12)

Полное уравнение можно свернуть к виду

,

что аналогично следующему:

В этой лекции не содержится полного описания корреляции. Предметом 8-й лекции является проблема оценивания по методу наименьших квадратов, которая тесно связана с корреляцией (см. раздел 8.4). В лекции 9 приведены коэффициенты корреляции для коррелированных данных, заданных в шкалах наименований и порядка.

Домашнее задание № 6

Вам необходимо, используя таблицу 7.2, вычеркнуть информацию о человеке, номер которого совпадает с Вашим номером по списку, а после этого определить коэффициент корреляции Пирсона для полученной группы из 39 человек (с точностью 4 значащих цифры).

№	ПІБ
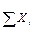
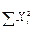
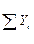
	Болховський Олексій Олександрович
	Гріциніна Людмила Сергіївна
	Гуля Леся Борисівна
	Дорда Ірина В'ячеславівна
	Кілядзе Анастасія Олександрівна
	Лі Мирослав Ігорович
	Ломакін Микита Володимирович
	Максименко Дмитро Олегович
	Моісєєнко Олексій Сергійович
	Непрелюк Олена Дмитрівна
	Павлюченко Антон Сергійович
	Паладян Юлія Олександрівна
	Петрова Олександра В’ячеславівна
	Скрипник Анастасія Ігорівна
	Ставська Тетяна Володимирівна
	Яковлєва Катерина Юріївна

ПРИЛОЖЕНИЯ

Дата добавления: 2014-10-22