Характеристика активной и реактивной ступени

Определение мощности ступени турбины

Сила, возникающая на лопатке под влиянием потока, определяется из уравне­ния механики (рис. 5.6.). Импульс силы равен количеству движения:

(5.10)

Импульс силы в единицу времени равен самой силе:

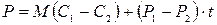(5.11)

Проекция силы на окружную скорость:

(5.12)

и осевую:

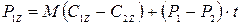(5.13)

Рис. 5.6. Силы, действующие на лопатки.

Крутящий момент определяется как произведение радиуса и силы (формула Эйлера):

(5.14)

Мощность, развиваемая ступенью, а, следовательно, и ГТУ:

(5.15)

Но и тогда:

(5.16)

Величина удельной работы (отнесенная к 1 кг рабочего тела на входе в ОК.)

(5.17)

Это уравнение справедливо для турбинной и компрессорной ступени и позво­ляет рассчитать мощность ГТУ.

Основной характеристикой ступени газовой турбины является её К.П.Д. Он представляет собой отношение фактического теплоперепада в ступени к теоре­тически возможному. В идеальной газовой турбине предполагают адиабатиче­ский теплоперепад без потерь кинетической энергии, в результате чего работа расширения, располагаемая работа, может быть преобразована в полезную ме­ханическую работу.

В реальной турбине часть располагаемой теплоты теряется. Работа идеально­го процесса в Т-S координатах представляет собой S_ab0c –количество подводи­мой теплоты. При нагревании рабочего тела в КС при Р = idem реальный про­цесс осуществляется по линии 0-1, и часть работы (теплоты) теряется вследст­вие необратимых потерь S_e11’b (рис. 5.7).

Рис.5.7. Работа реального и идеального процесса сжатия.

В h-S координатах коэффициент полезного действия ступени представляет собой отношение действительной работы h(02) к располагаемой h₀(02') (рис. 5.8).

(5.18)

Величина располагаемой работы определяется из уравнения истечения в адиабатном процессе. Если начальная скорость С₀ = 0 и не учитывается разность положения центра тяжести, то из уравнения истечения получаем:

(5.19)

а величина располагаемого перепада

Рис. 5.8. Сопоставление идеального и реального

процесса расширения.

Разность теплоперепадов h₀ – h = Δh – представляет собой величину потерь в ступени. Они (потери) представляют собой сумму потерь: потери энергии в направляющем аппарате, в рабочем колесе и с выходной скоростью (рис. 5.9).

· В направляющем аппарате

(5.20)

где h₁ – теплоперепад, соответствующий абсолютной скорости С| на входе в рабо­чее колесо; ξ – коэффициент потерь энергии.

· Δh ₂ = ξ ₂· h ₂ – теплоперепад в рабочем колесе.

· Δh ₃ = ξ ₃· h ₃ = – потери энергии с выходной скоростью. Причем, оказыва­ется, что Δh ₁ и Δh ₂, практически не зависят от скорости рабочего тела и остаются почти постоянными в рабочем диапазоне (ξ ₁и ξ ₂ определяются экспери­ментально).

Δh = Δh ₁ – Δh ₂ – Δh ₃

или

(5.21)

Для активной ступени турбины, учитывая, что ; φ – коэффициент скорости φ = .

Рис. 5.9. Коэффициент полезного действия ступени.

Выражение КПД ступени имеет вид:

(5.22)

,

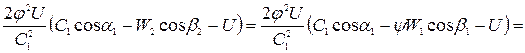
где W₁ = cos β₁ = C₁ cos α₁ – U.

Учитывая, что для активной ступени W₁ = W₂, но в связи с потерями W₁ = ψW₂ и из треугольников скоростей . Обозначая 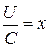получим:

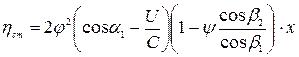(5.23)

Принимаем, что не зависят от х = . Определим максимум функции

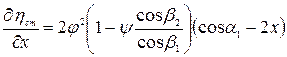(5.24)

т.е. 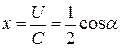. При α = 0, и при этих условиях К.П.Д. реактивной ступени имеет максимальное значение и

(5.25)

т.е. наибольшее значение КПД ступени получается, когда а = 0, т.к. U = 0,5 C. На практике а = 12-14°, т.к. меньшее значение получить трудно (малая толщина лопатки), то = 0,45-0,48 (рис. 5.8)

Для реактивной ступени рассмотрим частный случай, когда треугольники ско­ростей симметричны и следовательно C₁ = W₂ и W₁ = С₂, тогда:

(5.26)

и

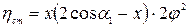(5.27)

и = х = cos α₁

т.е. при α = 0, = 1 рис. (5.10).

Максимальное значение КПД реактивной ступени с симметричными треуголь­никами скоростей получается при соотношении окружной и абсолютной скоро­стей равным 1. Эти соотношения используются для определения зоны эконо­мичной работы ступеней: активной и реактивной. Основными факторами, как видно из полученных соотношений является не величина скоростей, а их соот­ношение х = т.к. только при определенном значении К.П.Д. ступени дости­гает максимального значения. Причем оказывается, что существенное значение на К.П.Д. ступени оказывают коэффициенты скоростей φ и ψ.

Изменение К.П.Д. ступени при изменении φ при остальных неизменных величинах определяет­ся соотношением:

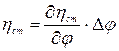
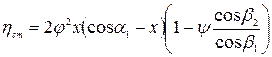
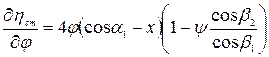(5.28)

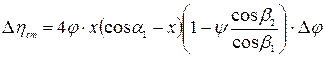
а относительное изменение:

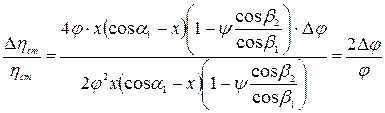(5.29)

Рис. 5.10. Коэффициенты полезного действия

активной и реактивной ступени турбины:

а) активная; б) реактивная.

Т.е. изменение коэффициента скорости φ вызывает изменение К.П.Д. ступени в два раза больше. Т.е. если φ меняется на 10 %, то η_ст на 20 %. Аналогичное влия­ние оказывает и коэффициент ψ,но его влияние в 4 раза меньше в связи с меньшим значением относительной скорости. Для обеспечения экономически выгодного режима работы турбины (в области работы ) в принципе безразлично, за счет чего изменяется величина окружной скорости. Следует заметить, что величина абсолютной скорости С₁ получается как результат преобразования теплоперепада в направляющем аппарате, и следовательно, характеризует работоспособность турбины (мощность N). Окружная скорость U характеризует быстроходность турбины (частоту враще­ния). В связи с тем, что эти величины имеют строго определенную зависи­мость, оказывается, что увеличение абсолютной скорости С₁ (увеличение теп­лоперепада и мощности) приводит к необходимости увеличивать частоту вра­щения (n). В современных ГТУ С₁ = 250 ÷ 350 м/с и выше, и следовательно, ок­ружные скорости 120-170 м/с, поэтому даже стационарные ГТУ работают как правило с большой частотой вращения (n = 5000-7000 об/мин). Причем оказы­вается, что при уменьшении частоты вращения и неизменном теплоперепаде резко меняется х = , и, следовательно, η_ст и η_е ГТУ. Именно этим объясня­ется высокая зависимость КПД ГТУ от частоты вращения. Наличие жесткой связи х = приводит к существованию предельного теплоперепада на ступе­ни, т.к. для сохранения х = = idem при повышении С₁ нельзя бесконечно увеличивать частоту вращения, т.к. лопатки турбины и так работают в жестких условиях (T₃^* = 750-1250). Причем оказывается, что для активной и реактивной ступени турбины при одинаковых частотах вращения в связи с различными значениями = 0,5; работоспособность (мощность) активных ступеней в 1,5-1,8 раза больше, чем у реактивных (теоретически в два раза), следовательно, при создании мощных турбин предпочтение, должно быть быть отдано активным ступеням, однако, газовые турбины, как правило, реактивные, при­чем степень реактивности возрастает по высоте лопатки, начиная от корня. Причиной этого является трудность осуществления активной ступени при на­личии длинных лопаток, когда между ними проходят большие потоки рабочего тела, кроме того К.П.Д. реактивных ступеней выше активных. В условиях, когда по турбине необходимо сработать большие значения теплоперепада, чем до­пустимые для одной ступени, газовые турбины выполняются многоступенча­тыми. При этом общий теплоперепад делят примерно на равные части между ступенями, которые выполняются как последовательные соединения этих сту­пеней в одном корпусе. Это дает возможность в одной многоступенчатой тур­бине реализовать большие значения теплоперепада при допустимых частотах вращения выходного вала и высоком общем значении К.П.Д. турбины.

Контрольные вопросы.

1. Перечислите основные элементы компрессорной ступени.

2. Что называют втулочным отношением ступени.

3. Какими параметрами характеризуется решетка профиля ступени?

4. При каком соотношении окружной и абсолютной скоростей достигается максимальный К.П.Д. реактивной ступени турбины?

5. Как влияют коэффициенты скоростей ψ и φ на К.П.Д. реактивной ступени турбины?

Дата добавления: 2014-10-22