Система статистичних показників

Характеристика середньої геометричної та середньої квадратичної величини.

Якщо визначальна властивість сукупності формується як добуток індивідуальних значень ознаки, використовується середня геометрична:

,

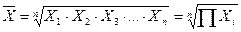де – символ добутку;

X_i – відносні величини динаміки, виражені кратним відношенням i-го значення показника до попереднього (i-1)-го.

Коли часові інтервали не однакові, розрахунок виконують за формулою середньої геометричної зваженої:

Найбільш широко використовується при аналізі динаміки з метою визначення середнього темпу зростання.

Середня квадратична використовується при визначенні показників варіації.

Середня квадратична проста:

Середня квадратична зважена:

Соціально-економічні явища надзвичайно складні й багатогранні. Будь-який показник відтворює лише одну грань предмета пізнання. Комплексна характеристика останнього передбачає використання системи показників, що має дві особливості:

1) всебічність кількісного відображення явищ;

2) органічний взаємозв’язок окремих показників, причому саме вони перетворюють групу показників на єдиний комплекс характеристик складного явища чи процесу.

Коло властивостей, що вивчаються, а отже, і показників системи залежить від мети дослідження. У кожній системі можна вирізнити певні множини показників, які детальніше відтворюють той чи інший бік явища. Систему показників визначають як ієрархічну структуру, на нижньому щаблі якої – узагальнюючий інтегральний показник, на верхньому – рівновагомі ознаки, які безпосередньо вимірюються.

Кожний показник системи має самостійне значення і водночас є складовою узагальнюючої властивості. Надмірна складність окремих суспільних явищ зумовила появу інтегральних комплексних оцінок, які обчислюються комбінуванням показників верхніх щаблів. Конструювання інтегральних оцінок ґрунтується на стандартизації показників, зведенні їх до одного виду. З-поміж інтегральних оцінок, побудованих на стандартизованій системі, широко використовуються рейтингові оцінки у вигляді багатовимірних середніх.

Суть багатовимірної середньої полягає в заміні індивідуальних значень множини показників j-го елемента сукупності Х_ij відносними величинами Р_ij. Базою порівняння можуть бути середні значення показників по сукупності в цілому або еталонні значення Х_i,st (норма, стандарт):

або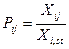

Багатовимірна середня – це середня арифметична з відношень Р_ij. Вона визначається для кожного j-го елемента і є інтегральною оцінкою певного явища саме для цього елемента:

,

де n – число показників.

Серед показників системи вирізняють стимулятори і де стимулятори. Показники-стимулятори свідчать про високий рівень i-го параметра при Р_ij>1, дестимулятори – при Р_ij<1. Щоб звести їх до однозначної характеристики, для дестимуляторів відношення Р_ij обчислюють як обернену величину.

Якщо показники вважаються рівно вагомими, кожному з них надається певна вага і розрахунок виконується за формулою середньої арифметичної зваженої:

,

де d_i – вага i-го показника.

Статистичний аналіз, що розкриває зміст і значення показників, поглиблюючи уявлення про предмет дослідження і властиві йому закономірності, виконують у двох напрямках:

1) замість ізольованих характеристик окремих сторін предмета розглядають зв’язки і відношення, виявляють фактори, які впливають на рівень і варіацію показників, оцінюють ефекти їх впливу;

2) вивчають динаміку показників, напрям і швидкість змін, визначають характер і рушійні сили розвитку.

Дата добавления: 2014-10-22