Пример 2. Макроэкономика. Рассмотрим экономический комплекс, состоящий их n секторов, выпускающих продукцию x1

Пример 1

Макроэкономика. Рассмотрим экономический комплекс, состоящий их n секторов, выпускающих продукцию x₁, x₂,..., x_n соответственно. Предположим для определенности, что выпуск продукции измеряется в долларах в год. Причем продукция, выпускаемая каждым сектором, используется как самим сектором, так и другими секторами комплекса и внешними потребителями.

Пусть a_ij представляет собой часть продукции, выпускаемой i-м сектором, которая необходима для производства единицы продукции j-го сектора (i, j = 1, 2,..., n). Внешнее потребление продукции, выпускаемой i-м сектором, обозначим через y_i. Тогда можно записать следующее уравнение материального баланса:

X_i ∑a_ijx_j + y_i

Данная элементарная модель может быть использована для определения объема продукции, необходимой для удовлетворения заданного спроса при существующей технологии, которая описывается с помощью коэффициентов a_ij. Возможные обобщения и детализация этой модели образуют основу для так называемой модели «затраты-выпуск». Матрицу технологических коэффициентов А=[a_ij] часто называют леонтьевской матрицей.

Динамика водохранилищ. Упрощенный вариант системы водохранилищ показан на рис.2.1. Выходами системы являются сток y₁(t) и доля грунтовых вод y₂(t) в этом стоке, внешними входами — осадки r₁(t) и r₂(t). Наполнение наземных водохранилищ в момент времени t обозначено через x₁(t),x₂(t) и x₃(t), наполнение подземного резервуара (с учетом просачивания) — через x₄(t), а попуски воды из водохранилищ — через u₁(t) и u₂(t). Учет связи между поверхностным стоком и грунтовыми водами осуществляется с помощью выражения l₃(x₄-x₃); коэффициент k характеризует поверхностный сток, а коэффициенты l₁ и l₂ — грунтовый.

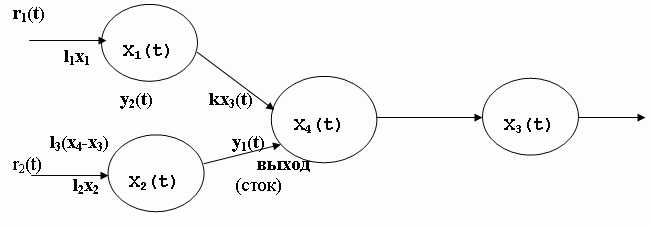
Рис. 2.1 — Сеть водохранилищ

Уравнения неразрывности приводят к следующим динамическим соотношениям:

x₁(t+1) = x₁(t) - l₁x₁(t) - u₁(t) + r₁(t),
x₂(t+1) = x₂(t) - l₂x₂(t) - u₂(t) + r₂(t),
x₃(t+1) = x₃(t) + l₃[x₄(t) - x₃(t)] - kx₃(t) + u₁(t) + u₂(t),
x₄(t+1) = x₄(t) + l₁x₁(t) + l₂x₂(t) - l₃[x₄(t) - x₃(t)].

Измеряемые выходы системы имеют вид:

y₁(t) = kx₃(t),
y₂(t) = l₃[x₄(t) - x₃(t)].

Приведенное выше описание системы может оказаться полезным при изучении ряда важных вопросов, связанных с управлением паводками, оптимальной стратегией попусков (водосборов), точным определением уровня грунтовых вод и т.д.

Дата добавления: 2014-10-15