
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Элементы теории множеств
|
|
|
|
Множеством называется любое объединение определённых, вполне различимых объектов; их может и не быть вообще. Можно говорить о множестве точек на отрезке [0,1], множестве студентов в группе, множестве снежных дней в июле на экваторе, т.е. множество образуют любые объекты, объединённые по любому признаку. Объекты, составляющие множество, называются элементами множества. Множество, не имеющее ни одного элемента, называется пустым, обозначается Ø. Множество, состоящее из конечного числа элементов, называется конечным, в противном случае – бесконечным.
Задать множество можно перечислением его элементов. Например, множество, образованное из n элементов а 1, а 2, ..., аn, обозначается А = { а1, а2,..., аn }; пишется а 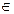 А (говорится «элемент а при надлежит множеству А»), если а является элементом множества А, в противном случае a
А (говорится «элемент а при надлежит множеству А»), если а является элементом множества А, в противном случае a 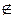 A. Задать множество можно также, указав общее свойство для всех его и только его элементов. Например, множество равноудалённых от концов отрезка точек. Два множества считаются равными, если состоят из одних и тех же элементов; записывается А = В. Множество B называется подмножеством А (записывается B Ì А), если все элементы множества А 1 являются элементами А.
A. Задать множество можно также, указав общее свойство для всех его и только его элементов. Например, множество равноудалённых от концов отрезка точек. Два множества считаются равными, если состоят из одних и тех же элементов; записывается А = В. Множество B называется подмножеством А (записывается B Ì А), если все элементы множества А 1 являются элементами А.
Для множеств определены следующие операции: объединение, пересечение, дополнение. Объединением множеств А и В (записывается A È B) называется множество, состоящее из элементов как одного, так и второго множества. Например, А и В – множества точек, принадлежащих некоторым двум кругам, имеющим общие точки, тогда объединением A È B будет фигура, состоящая из общих точек. Пересечением множеств А и В (записывается А Ç В) называется множество, состоящее из элементов, принадлежащих как одному, так и второму множеству одновременно. Дополнением множества А до В называется множество, состоящее из элементов множества В, не принадлежащих А. Дополнение обозначается C = В - А (рис. 3.1).
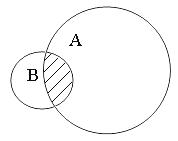 АÇВ
АÇВ
| 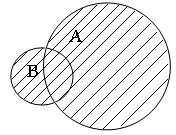 АÈВ
АÈВ
|  В-А
В-А
|
Рис. 3.1. Операции над множествами
|
|
|
|
|
Дата добавления: 2014-10-22; Просмотров: 345; Нарушение авторских прав?; Мы поможем в написании вашей работы!