Алгоритмы линейной структуры

Альтернатива (ветвление);

Базовые управляющие структуры алгоритмов (основные алгоритмические конструкции)

Метод структурной алгоритмизации. Этот метод основан на визуальном представлении алгоритма в виде последовательности управляющих структурных элементов − управляющих структур. Принцип структурной алгоритмизации заключается в том, чтологическая структура любой программы может быть выражена комбинацией из следующих базовых структур:

1 ) Композиция (следование);

3) Итерация [2] (цикл).

Структурная блок-схема − композиция из базовых алгоритмических структур.

Примем следующие обозначения: S 1 и S 2 представляют собой в общем случае операции, группы операций или алгоритмические структуры (базовые управляющие структуры) для соответствующего исполнителя, В – это условие, в зависимости от истинности (true) или ложности (false) которого управление передаётся по одной из двух ветвей.

Композиция, или следование − это линейная конструкция алгоритма, составленная из последовательно следующих друг за другом функциональных вершин (рис. 9.2).

Операции, группы операций или базовые структуры алгоритмов выполняются последовательно друг за другом.

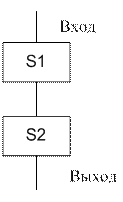
Рис. 9.2. Базовая управляющая структура «следование»

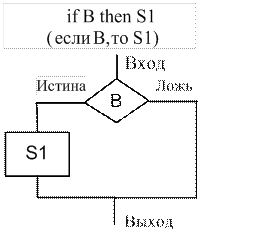
Альтернатива, или ветвление – это конструкция ветвления, имеющая предикатную вершину.

Структура обеспечивает выбор между двумя альтернативами: если B – ИСТИНА (TRUE) (не равно нулю), то выполняется структура S 1; если B – ЛОЖЬ (FALSE) – структура S 2 (рис. 9.3). При этом происходит разветвление алгоритма.

Если в структуре «Ветвление» отсутствует операция, группа операций или алгоритмическая структура S 2, которую необходимо выполнить при ложности выражения B, получается сокращённая форма структуры «Ветвление» (рис. 9.4), которую ещё называют структурой «Обход».

Рис. 9.3. Базовая управляющая структура «Ветвление»	Рис. 9.4. Сокращённая форма структуры «Ветвление»

Итерация, или циклы – это циклическая конструкция алгоритма, состоящая из композиции и альтернативы.

Алгоритмическая структура (базовая управляющая структура) «Итерация, или цикл» может быть представлена в двух формах: с предусловием (рис. 9.5) и с постусловием (рис. 9.6).

Цикл представляет собой повторное выполнение определённого набора действий при выполнении некоторого условия. Именно циклы позволяют записывать длинные последовательности операций небольшим числом команд.

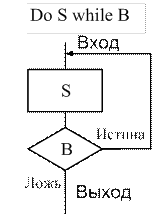
В цикле с постусловием типа «ДО»(рис. 9.5) проверка условия выхода из цикла выполняется после очередного действия. Цикл«ДО»выполняется до тех пор, пока условие не станет истинным.

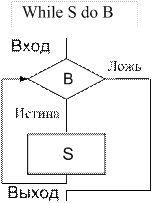
На рисунке 9.6 показан цикл типа«ПОКА» с предусловием. Действия внутри этого цикла повторяются, пока выражение B в блоке ветвления истинно, причём сначала проверяется условие, а затем выполняется действие S.

Обязательными блоками в этих структурах являются: установка начального значения параметра; проверка условия достижения конечного значения параметра; изменение параметра. Отличаются они способом проверки окончания цикла.

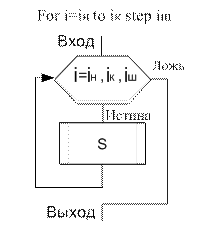
Цикл типа«ДЛЯ», или цикл с параметром (рис. 9.7) является модификацией цикла «ПОКА» для ситуации, когда заранее известно количество повторений некоторых действий. Все три необходимых блока собираются в один, в котором указывается начальное, конечное значение параметра и шаг изменения. Запись в блоке заголовка цикла на рисунке 9.7 показывает пример описания заголовка цикла, в котором действия повторяются столько раз, сколько целых значений приобретает параметр цикла i от своего начального значения i _н до конечного i _к с шагом i _ш. Шаг не указывается, если он равен 1.

Рис. 9.5. Структура «ЦИКЛ-ДО» (цикл с постусловием)	Рис. 9.6. Структура «ЦИКЛ-ПОКА»(цикл с предусловием)	Рис. 9.7. Цикл с параметром (использование символа «подготовка»)

В соответствии с наличием в алгоритмах управляющих структур композиции, альтернативы и итерации алгоритмы классифицируют: на линейные, разветвлённые и циклические алгоритмы.

Линейные алгоритмы предполагают последовательное выполнение действий в порядке, заданном схемой, без их повторения или пропуска некоторых действий. Алгоритм линейной структуры изображается линейной последовательностью связанных друг с другом блоков (рис. 9.8). Такой порядок выполнения действий называется естественным. Поэтому в схемах алгоритмов линейной структуры нет блока «Решение».

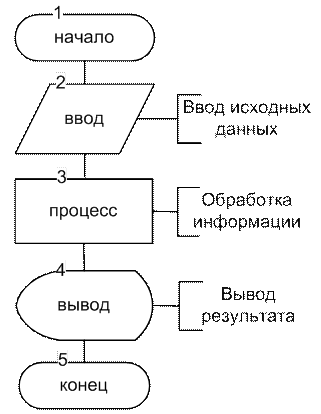
Рис. 9.8. Алгоритм линейной структуры

В тестовом задании ниже представлен линейный вычислительный процесс. Фрагмент данного алгоритма записан в словесно-формульном виде.

Тестовое задание 9.7.

Чему равны значения переменных а и b после выполнения следующего фрагмента алгоритма:

1) а = 3;

2) b = 7;

3) b = a;

4) a = b;

5) b = b*2

Ответы:

6) a = 3; b = 6

7) a = 14; b = 7

8) a = 7; b = 14

9) a = 6; b = 3

10) a = 3; b = 14

Решение. Выполняем алгоритм последовательно по шагам:

1) а = 3;

2) b = 7;

3) b = a; знак равенства «=» в этом случае трактуется как знак присваивания «=:», следовательно, переменной b присваивается значение переменной а=3; т.е. переменная b примет значение b=3;

4) a=b; переменной а присваивается значение переменной b=3; следовательно, переменная а примет значение а =3;

5) b=b*2; переменной b присваивается значение b*2 ( к этому моментупеременная b имеет значение b=3); следовательно, переменная b примет значение b= b·2=3·2=6.

Таким образом, в результате выполнения алгоритма переменные а и b примут значения a = 3; b = 6.

Визуальное представление данного фрагмента алгоритма в виде блок-схемы представлено на рисунке 9.9.

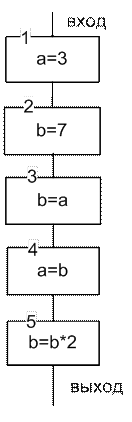
Рис. 9.9. Визуальное представление фрагмента линейного алгоритма

Дата добавления: 2014-10-22